2.2: Solve Equations using the Division and Multiplication Properties of Equality
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Solve equations using the Division and Multiplication Properties of Equality
- Solve equations that require simplification
- Translate to an equation and solve
- Translate and solve applications
Before you get started, take this readiness quiz.
- Simplify: −7(\frac{1}{-7}).
If you missed this problem, review Exercise 1.6.13. - Evaluate 9x+2 when x=−3.
If you missed this problem, review Exercise 1.5.34.
Solve Equations Using the Division and Multiplication Properties of Equality
You may have noticed that all of the equations we have solved so far have been of the form x+a=b or x−a=b. We were able to isolate the variable by adding or subtracting the constant term on the side of the equation with the variable. Now we will see how to solve equations that have a variable multiplied by a constant and so will require division to isolate the variable.
Let’s look at our puzzle again with the envelopes and counters in Figure \PageIndex{1}.
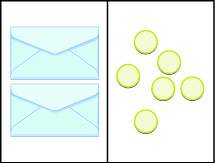
In the illustration there are two identical envelopes that contain the same number of counters. Remember, the left side of the workspace must equal the right side, but the counters on the left side are “hidden” in the envelopes. So how many counters are in each envelope?
How do we determine the number? We have to separate the counters on the right side into two groups of the same size to correspond with the two envelopes on the left side. The 6 counters divided into 2 equal groups gives 3 counters in each group (since 6\div 2=3).
What equation models the situation shown in Figure \PageIndex{2}? There are two envelopes, and each contains xx counters. Together, the two envelopes must contain a total of 6 counters.
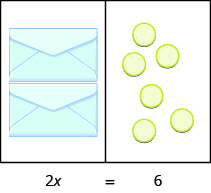
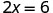 |
|
| If we divide both sides of the equation by 2, as we did with the envelopes and counters, | 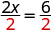 |
| we get: | 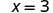 |
We found that each envelope contains 3 counters. Does this check? We know 2\cdot 3=6, so it works! Three counters in each of two envelopes does equal six!
This example leads to the Division Property of Equality.
For any numbers a, b, and c, and c\neq 0,
\begin{array} {llll} {\text { If }} &{a} &{=} &{b} \\ {\text {then}} & {\frac { a } { c }} &{=} &{\frac { b } { c }} \end{array}
When you divide both sides of an equation by any non-zero number, you still have equality.
Doing the Manipulative Mathematics activity “Division Property of Equality” will help you develop a better understanding of how to solve equations by using the Division Property of Equality.
The goal in solving an equation is to ‘undo’ the operation on the variable. In the next example, the variable is multiplied by 5, so we will divide both sides by 5 to ‘undo’ the multiplication.
Solve: 5x=−27.
Solution
| To isolate x, “undo” the multiplication by 5. | 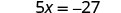 |
|
| Divide to ‘undo’ the multiplication. | 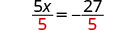 |
|
| Simplify. | 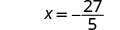 |
|
| Check: | 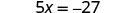 |
|
| Substitute -\frac{27}{5} for x. | 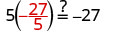 |
|
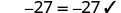 |
||
| Since this is a true statement, x = -\frac{27}{5} is the solution to 5x=−27. |
||
Solve: 3y=−41.
- Answer
-
y = -\frac{41}{3}
Solve: 4z=−55.
- Answer
-
y = -\frac{55}{4}
Consider the equation \frac{x}{4} = 3. We want to know what number divided by 4 gives 3. So to “undo” the division, we will need to multiply by 4. The Multiplication Property of Equality will allow us to do this. This property says that if we start with two equal quantities and multiply both by the same number, the results are equal.
For any numbers a, b, and c,
\begin{array} {llll} {\text {If}} &{a} & {=} &{b} \\ {\text {then}} &{a c} &{=} &{b c} \end{array}
If you multiply both sides of an equation by the same number, you still have equality.
Solve: \frac{y}{-7} = -14
Solution
Here y is divided by −7. We must multiply by −7 to isolate y.
| \frac{y}{-7} = -14 | ||
| Multiply both sides by −7. | 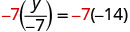 |
|
| Multiply. | 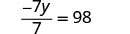 |
|
| Simplify. | 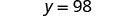 |
|
| Check: \frac{y}{-7} = -14 | ||
| Substitute y=98. | \dfrac{\color{red}{98}}{-7} \stackrel{?}{=} -14 | |
| Divide. | 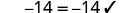 |
|
Solve: \frac{a}{-7} = -42
- Answer
-
a = 294
Solve: \frac{b}{-6} = -24
- Answer
-
b = 144
Solve: -n = 9
Solution
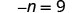 |
||
| Remember −n is equivalent to −1n. | 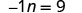 |
|
| Divide both sides by −1. | 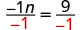 |
|
| Divide. | 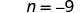 |
|
| Notice that there are two other ways to solve −n=9. We can also solve this equation by multiplying both sides by −1 and also by taking the opposite of both sides. | ||
| Check: | 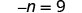 |
|
| Substitute n=−9. | 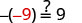 |
|
| Simplify. | 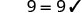 |
|
Solve: −k=8.
- Answer
-
k = -8
Solve: −g=3.
- Answer
-
g = -3
Solve: \frac{3}{4}x = 12
Solution
Since the product of a number and its reciprocal is 1, our strategy will be to isolate x by multiplying by the reciprocal of \frac{3}{4}.
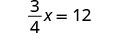 |
||
| Multiply by the reciprocal of \frac{3}{4}. | 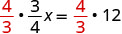 |
|
| Reciprocals multiply to 1. | 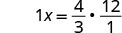 |
|
| Multiply. | 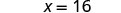 |
|
| Notice that we could have divided both sides of the equation \frac{3}{4}x = 12 by \frac{3}{4} to isolate x. While this would work, most people would find multiplying by the reciprocal easier. | ||
| Check: | 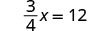 |
|
| Substitute x=16. | 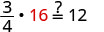 |
|
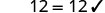 |
||
Solve: \frac{2}{5}n=14.
- Answer
-
n = 35
Solve: \frac{5}{6}y=15.
- Answer
-
y = 18
In the next example, all the variable terms are on the right side of the equation. As always, our goal in solving the equation is to isolate the variable.
Solve: \frac{8}{15} = -\frac{4}{5}x
Solution
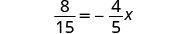 |
||
| Multiply by the reciprocal of -\frac{4}{5}. | 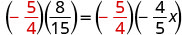 |
|
| Reciprocals multiply to 1. | 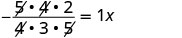 |
|
| Multiply. | 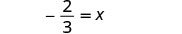 |
|
| Check: | 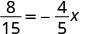 |
|
| Let x = -\frac{2}{3}. | 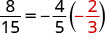 |
|
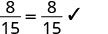 |
||
Solve: \frac{9}{25} = -\frac{4}{5}z
- Answer
-
z = - \frac{9}{5}
\frac{5}{6} = -\frac{8}{3}r
- Answer
-
r = -\frac{5}{16}
Solve Equations That Require Simplification
Many equations start out more complicated than the ones we have been working with.
With these more complicated equations the first step is to simplify both sides of the equation as much as possible. This usually involves combining like terms or using the distributive property.
Solve: 14−23=12y−4y−5y.
Solution
Begin by simplifying each side of the equation.
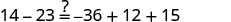 |
||
| Simplify each side. | 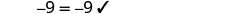 |
|
| Divide both sides by 3 to isolate y. | 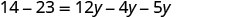 |
|
| Divide. |  |
|
| Check: | 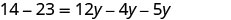 |
|
| Substitute y=−3. | 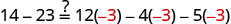 |
|
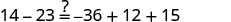 |
||
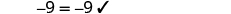 |
||
Solve: 18−27=15c−9c−3c.
- Answer
-
c=−3
Solve: 18−22=12x−x−4x.
- Answer
-
x = -\frac{4}{7}
Solve: −4(a−3)−7=25.
Solution
Here we will simplify each side of the equation by using the distributive property first.
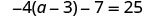 |
||
| Distribute. | 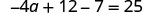 |
|
| Simplify. | 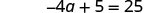 |
|
| Simplify. | 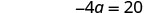 |
|
| Divide both sides by -4 to isolate a. | 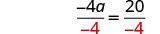 |
|
| Divide. |  |
|
| Check: |  |
|
| Substitute a = -5 | 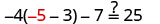 |
|
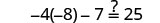 |
||
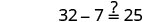 |
||
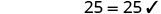 |
||
Solve: −4(q−2)−8=24.
- Answer
-
q=−6
Solve: −6(r−2)−12=30.
- Answer
-
r=−5
Now we have covered all four properties of equality—subtraction, addition, division, and multiplication. We’ll list them all together here for easy reference.
When you add, subtract, multiply, or divide the same quantity from both sides of an equation, you still have equality.
\begin{array} {ll} {\textbf {Subtraction Property of Equality}} &{\textbf{Addition Property of Equality}} \\ {\text{For any real numbers a, b, and c,}} &{\text{For any real numbers a, b, and c,}} \\ {\text{if }a = b,} &{\text{if }a = b,} \\ {\text{then }a - c = b - c} &{\text{then }a + c = b + c} \\ {\textbf {Divition Property of Equality}} &{\textbf{Multiplication Property of Equality}} \\ {\text{For any real numbers a, b, and c,}} &{\text{For any real numbers a, b, and c,}} \\ {\text{if }a = b,} &{\text{if }a = b,} \\ {\text{then }a - c = b - c} &{\text{then }a + c = b + c} \end{array}
When you add, subtract, multiply, or divide the same quantity from both sides of an equation, you still have equality.
Translate to an Equation and Solve
In the next few examples, we will translate sentences into equations and then solve the equations. You might want to review the translation table in the previous chapter.
Translate and solve: The number 143 is the product of −11 and y.
Solution
| Translate. |  |
| Divide by −11. | 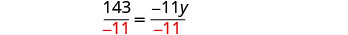 |
| Simplify. |  |
| Check: \begin{array} {lll} {143} &{=} &{-11y} \\ {143} &{\stackrel{?}{=}} &{-11(-13)} \\ {143} &{=} &{143\checkmark} \end{array} |
Translate and solve: The number 132 is the product of −12 and y.
- Answer
-
132=−12y;y=−11
Translate and solve: The number 117 is the product of −13 and z.
- Answer
-
117=−13z;z=−9
Translate and solve: n divided by 8 is −32.
Solution
| Begin by translating the sentence into an equation. Translate. |
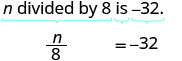 |
|
| Multiple both sides by 8. | 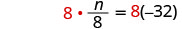 |
|
| Simplify. | 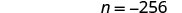 |
|
| Check: | Is nn divided by 8 equal to −32? | |
| Let n=−256. | Is −256 divided by 88 equal to −32? | |
| Translate. | \frac{-256}{8} \stackrel{?}{=} -32 | |
| Simplify. | −32=−32\checkmark | |
Translate and solve: nn divided by 7 is equal to −21.
- Answer
-
\frac{n}{7}=−21; n=−147
Translate and solve: n divided by 8 is equal to −56.
- Answer
-
\frac{n}{8}=−56;n=−448
Translate and solve: The quotient of yy and −4 is 68.
Solution
Begin by translating the sentence into an equation.
| Translate. | 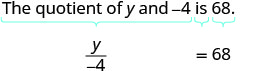 |
|
| Multiply both sides by -4. |  |
|
| Simplify. |  |
|
| Check: | Is the quotient of y and −4 equal to 68? | |
| Let y=−272. | Is the quotient of −272 and −4 equal to 68? | |
| Translate. | \frac{-272}{-4} \stackrel{?}{=} 68 | |
| Simplify. | 68 = 68\checkmark | |
Translate and solve: The quotient of q and −8 is 72.
- Answer
-
\frac{q}{-8}=72;q=−576
Translate and solve: The quotient of p and −9 is 81.
- Answer
-
\frac{p}{-9}=81;p=−729
Translate and solve: Three-fourths of p is 18.
Solution
Begin by translating the sentence into an equation. Remember, “of” translates into multiplication.
| Translate. | 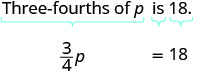 |
|
| Multiply both sides by \frac{4}{3}. | 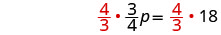 |
|
| Simplify. |  |
|
| Check: | Is three-fourths of p equal to 18? | |
| Let p = 24. | Is three-fourths of 24 equal to 18? | |
| Translate. | \frac{3}{4}\cdot 24 \stackrel{?}{=} 18 | |
| Simplify. | 18=18\checkmark | |
Translate and solve: Two-fifths of f is 16.
- Answer
-
\frac{2}{5}f=16; f=40
Translate and solve: Three-fourths of f is 21.
- Answer
-
\frac{3}{4}f=21; f=28
Translate and solve: The sum of three-eighths and x is one-half.
Solution
Begin by translating the sentence into an equation.
| Translate. | 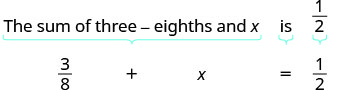 |
|
| Subtract \frac{3}{8} from each side. |  |
|
| Simplify and rewrite fractions with common denominators. |  |
|
| Simplify. |  |
|
| Check: | Is the sum of three-eighths and x equal to one-half? | |
| Let x=\frac{1}{8}. | Is the sum of three-eighths and one-eighth equal to one-half? | |
| Translate. | \frac{3}{8} + \frac{1}{8} \stackrel{?}{=} \frac{1}{2} | |
| Simplify. | \frac{4}{8} \stackrel{?}{=} \frac{1}{2} | |
| Simplify. | \frac{1}{2} = \frac{1}{2} \checkmark | |
Translate and solve: The sum of five-eighths and x is one-fourth.
- Answer
-
\frac{5}{8} + x = \frac{1}{4}; x = -\frac{3}{8}
Translate and solve: The sum of three-fourths and x is five-sixths.
- Answer
-
\frac{3}{4} + x = \frac{5}{6}; x = \frac{1}{12}
Translate and Solve Applications
To solve applications using the Division and Multiplication Properties of Equality, we will follow the same steps we used in the last section. We will restate the problem in just one sentence, assign a variable, and then translate the sentence into an equation to solve.
Denae bought 6 pounds of grapes for $10.74. What was the cost of one pound of grapes?
Solution
\begin{array} {ll} {\text{What are you asked to find?}} &{\text{The cost of 1 pound of grapes}} \\\\ {\text{Assign a variable.}} &{\text{Let c = the cost of one pound.}} \\\\ {\text{Write a sentence that gives the}} &{\text{The cost of 6 pounds is }$10.74} \\ {\text{information to find it.}} &{} \\\\ {\text{Translate into an equation.}} &{6c = 10.74} \\ {\text{Solve.}} &{\frac{6c}{c} = \frac{10.74}{6}} \\ {} &{c = 1.79} \\\\ {} &{\text{The grapes cost }$ 1.79 \text{ per pound.}} \\ \\ {\text{Check: If one pound costs }$1.79, do} &{} \\ {\text{6 pounds cost }$ 10.74?} &{} \\\\ {6(1.79) \stackrel{?}{=} 10.74} &{} \\ {10.74 = 10.74\checkmark} &{} \end{array}
Translate and solve:
Arianna bought a 24-pack of water bottles for $9.36. What was the cost of one water bottle?
- Answer
-
$0.39
Translate and solve:
At JB’s Bowling Alley, 6 people can play on one lane for $34.98. What is the cost for each person?
- Answer
-
$5.83
Andreas bought a used car for $12,000. Because the car was 4-years old, its price was \frac{3}{4} of the original price, when the car was new. What was the original price of the car?
Solution
\begin{array} {ll} {\text{What are you asked to find?}} &{\text{The original price of the car}} \\\\ {\text{Assign a variable.}} &{\text{Let p = the original price.}} \\\\ {\text{Write a sentence that gives the}} &{$12000\text{ is }\frac{3}{4} \text{ of the original price.}} \\ {\text{information to find it.}} &{} \\\\ {\text{Translate into an equation.}} &{12000 = \frac{3}{4}p} \\ {} &{\frac{3}{4}(12000) = \frac{4}{3}\cdot \frac{3}{4}p}\\ {}&{16000 = p} \\{\text{Solve.}} &{} \\\\ {} &{\text{The original cost of the car was }$ 16000.} \\ \\ {\text{Check: Is }\frac{3}{4} \text{ of }$16000 \text{ equal to }$12000} &{} \\\\ {\frac{3}{4}\cdot 16000 \stackrel{?}{=} 12000} &{} \\ {12000 = 12000\checkmark} &{} \end{array}
Translate and solve:
The annual property tax on the Mehta’s house is $1,800, calculated as \frac{15}{1000} of the assessed value of the house. What is the assessed value of the Mehta’s house?
- Answer
-
$120000
Translate and solve:
Stella planted 14 flats of flowers in \frac{2}{3} of her garden. How many flats of flowers would she need to fill the whole garden?
- Answer
-
21 flats
Key Concepts
- The Division Property of Equality—For any numbers a, b, and c, and c\neq 0, if a=b, then \frac{a}{c} = \frac{b}{c}.
When you divide both sides of an equation by any non-zero number, you still have equality. - The Multiplication Property of Equality—For any numbers a, b, and c, if a=b, then ac = bc.
If you multiply both sides of an equation by the same number, you still have equality.


