6.3: Multiply Polynomials
- Page ID
- 15160
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Multiply a polynomial by a monomial
- Multiply a binomial by a binomial
- Multiply a trinomial by a binomial
Before you get started, take this readiness quiz.
- Distribute: \(2(x+3)\).
If you missed this problem, review Example 1.10.31. - Combine like terms: \(x^{2}+9x+7x+63\).
If you missed this problem, review Example 1.3.37.
Multiply a Polynomial by a Monomial
We have used the Distributive Property to simplify expressions like \(2(x−3)\). You multiplied both terms in the parentheses, \(x\) and \(3\), by \(2\), to get \(2x−6\). With this chapter’s new vocabulary, you can say you were multiplying a binomial, \(x−3\), by a monomial, \(2\).
Multiplying a binomial by a monomial is nothing new for you! Here’s an example:
Multiply: \(4(x+3)\).
Solution
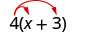 |
|
| Distribute. | \(4 \cdot x+4 \cdot 3\) |
| Simplify. | \(4 x+12\) |
Multiply: \(5(x+7)\).
- Answer
-
5x+35
Multiply: \(3(y+13)\).
- Answer
-
3y+39
Multiply: y(y−2).
Solution
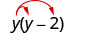 |
|
| Distribute. | \(y \cdot y-y \cdot 2\) |
| Simplify. | \(y^{2}-2 y\) |
Multiply: \(x(x−7)\).
- Answer
-
\(x^{2}-7 x\)
Multiply: \(d(d−11)\).
- Answer
-
\(d^{2}-11d\)
Multiply: \(7x(2 x+y)\)
Solution
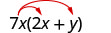 |
|
| Distribute. | 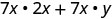 |
| Simplify. | 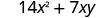 |
Multiply: \(5x(x+4 y)\)
- Answer
-
\(5 x^{2}+20 x y\)
Multiply: \(2p(6 p+r)\)
- Answer
-
\(12 p^{2}+2 p r\)
Multiply: \(-2 y\left(4 y^{2}+3 y-5\right)\)
Solution
 |
|
| Distribute. | 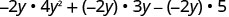 |
| Simplify. | 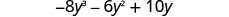 |
Multiply: \(-3 y\left(5 y^{2}+8 y-7\right)\)
- Answer
-
\(-15 y^{3}-24 y^{2}+21 y\)
Multiply: \(4x^{2}\left(2 x^{2}-3 x+5\right)\)
- Answer
-
\(8 x^{4}-24 x^{3}+20 x^{2}\)
Multiply: \(2x^{3}\left(x^{2}-8 x+1\right)\)
Solution
 |
|
| Distribute. | \(2 x^{3} \cdot x^{2}+\left(2 x^{3}\right) \cdot(-8 x)+\left(2 x^{3}\right) \cdot 1\) |
| Simplify. | \(2 x^{5}-16 x^{4}+2 x^{3}\) |
Multiply: 4\(x\left(3 x^{2}-5 x+3\right)\)
- Answer
-
\(12 x^{3}-20 x^{2}+12 x\)
Multiply: \(-6 a^{3}\left(3 a^{2}-2 a+6\right)\)
- Answer
-
\(-18 a^{5}+12 a^{4}-36 a^{3}\)
Multiply: \((x+3) p\)
Solution
| The monomial is the second factor. |  |
| Distribute. | \(x \cdot p+3 \cdot p\) |
| Simplify. | \( x p+3 p \) |
Multiply: \((x+8) p\)
- Answer
-
\(x p+8 p\)
Multiply: \((a+4) p\)
- Answer
-
\(a p+4 p\)
Multiply a Binomial by a Binomial
Just like there are different ways to represent multiplication of numbers, there are several methods that can be used to multiply a binomial times a binomial. We will start by using the Distributive Property.
Multiply a Binomial by a Binomial Using the Distributive Property
Look at Example \(\PageIndex{16}\), where we multiplied a binomial by a monomial.
| Instructions | Expression |
|---|---|
| Starting Expressions |  |
| We distributed the \(p\) to get: | 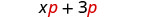 |
| What if we have \((x + 7)\) instead of \(p\)? |  |
| Distribute \((x + 7)\). | 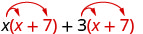 |
| Distribute again. | \(x^{2}+7 x+3 x+21\) |
| Combine like terms. | \(x^{2}+10 x+21\) |
Notice that before combining like terms, you had four terms. You multiplied the two terms of the first binomial by the two terms of the second binomial—four multiplications.
Multiply: \((y+5)(y+8)\)
Solution
 |
|
| Distribute (y + 8). | 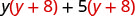 |
| Distribute again | \(y^{2}+8 y+5 y+40\) |
| Combine like terms. | \( y^{2}+13 y+40 \) |
Multiply: \((x+8)(x+9)\)
- Answer
-
\(x^{2}+17 x+72\)
Multiply: \((5 x+9)(4 x+3)\)
- Answer
-
\(20 x^{2}+51 x+27\)
Multiply: \((2 y+5)(3 y+4)\)
Solution
 |
|
| Distribute (3y + 4). | 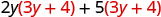 |
| Distribute again | \(6 y^{2}+8 y+15 y+20\) |
| Combine like terms. | \(6 y^{2}+23 y+20\) |
Multiply: \((3 b+5)(4 b+6)\)
- Answer
-
\(12 b^{2}+38 b+30\)
Multiply: \((a+10)(a+7)\)
- Answer
-
\(a^{2}+17 a+70\)
Multiply: \((4 y+3)(2 y-5)\)
Solution
 |
|
| Distribute. | 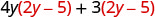 |
| Distribute again. | \(8 y^{2}-20 y+6 y-15\) |
| Combine like terms. | \(8 y^{2}-14 y-15\) |
Multiply: \((5 y+2)(6 y-3)\)
- Answer
-
\(30 y^{2}-3 y-6\)
Multiply: \((3 c+4)(5 c-2)\)
- Answer
-
\(15 c^{2}+14 c-8\)
Multiply: \((x-2)(x-y)\)
Solution
 |
|
| Distribute. |  |
| Distribute again. | \(x^{2}-x y-2 x+2 y\) |
| There are no like terms to combine. |
Multiply: \((a+7)(a-b)\)
- Answer
-
\(a^{2}-a b+7 a-7 b\)
Multiply: \((x+5)(x-y)\)
- Answer
-
\(x^{2}-x y+5 x-5 y\)
Multiply a Binomial by a Binomial Using the FOIL Method
Remember that when you multiply a binomial by a binomial you get four terms. Sometimes you can combine like terms to get a trinomial, but sometimes, like in Example \(\PageIndex{28}\), there are no like terms to combine.
Let’s look at the last example again and pay particular attention to how we got the four terms.
\[\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y}\end{array} \nonumber\]
Where did the first term, \(x^{2}\), come from?

We abbreviate “First, Outer, Inner, Last” as FOIL. The letters stand for ‘First, Outer, Inner, Last’. The word FOIL is easy to remember and ensures we find all four products.
\[\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y} \\ {F \qquad O\qquad I\qquad L}\end{array}\]
Let’s look at (x+3)(x+7).
| Distributive Property | FOIL |
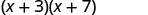 |
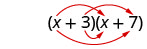 |
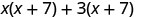 |
|
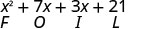 |
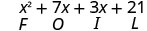 |
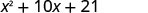 |
\(x^{2}+10 x+21\) |
Notice how the terms in third line fit the FOIL pattern.
Now we will do an example where we use the FOIL pattern to multiply two binomials.
Multiply using the FOIL method: \((x+5)(x+9)\)
Solution

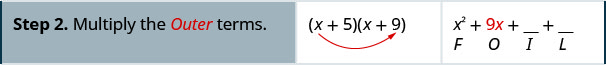
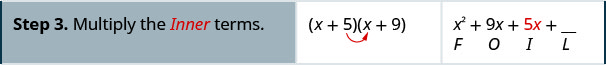
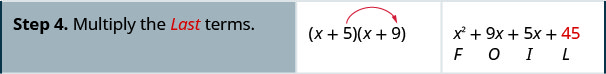

Multiply using the FOIL method: \((x+6)(x+8)\)
- Answer
-
\(x^{2}+14 x+48\)
Multiply using the FOIL method: \((y+17)(y+3)\)
- Answer
-
\(y^{2}+20 y+51\)
We summarize the steps of the FOIL method below. The FOIL method only applies to multiplying binomials, not other polynomials!

When you multiply by the FOIL method, drawing the lines will help your brain focus on the pattern and make it easier to apply.
Multiply: \((y−7)(y+4)\).
Solution

Multiply: \((x−7)(x+5)\).
- Answer
-
\(x^{2}-2 x-35\)
Multiply: (b−3)(b+6).
- Answer
-
\(b^{2}+3 b-18\)
Multiply: \((4x+3)(2x−5)\).
Solution

Multiply: \((3x+7)(5x−2)\).
- Answer
-
\(15 x^{2}+29 x-14\)
Multiply: \((4y+5)(4y−10)\).
- Answer
-
\(16 y^{2}-20 y-50\)
The final products in the last four examples were trinomials because we could combine the two middle terms. This is not always the case.
Multiply: \((3x−y)(2x−5)\).
Solution
| \((3 x-y)(2 x-5)\) | |
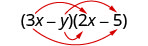 |
|
| Multiply the First. | 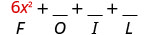 |
| Multiply the Outer. | 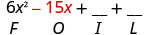 |
| Multiply the Inner. | 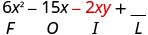 |
| Multiply the Last. | 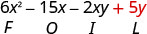 |
| Combine like terms—there are none. | \(6 x^{2}-15 x-2 x y+5 y\) |
Multiply: (10c−d)(c−6).
- Answer
-
\(10 c^{2}-60 c-c d+6 d\)
Multiply: (7x−y)(2x−5).
- Answer
-
\(14 x^{2}-35 x-2 x y+10 y\)
Be careful of the exponents in the next example.
Multiply: \(\left(n^{2}+4\right)(n-1)\)
Solution
| \(\left(n^{2}+4\right)(n-1)\) | |
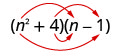 |
|
| Multiply the First. | 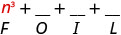 |
| Multiply the Outer. | 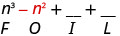 |
| Multiply the Inner. | 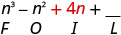 |
| Multiply the Last. | 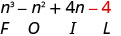 |
| Combine like terms—there are none. | \( n^{3}-n^{2}+4 n-4 \) |
Multiply: \(\left(x^{2}+6\right)(x-8)\)
- Answer
-
\(x^{3}-8 x^{2}+6 x-48\)
Multiply: \(\left(y^{2}+7\right)(y-9)\)
- Answer
-
\(y^{3}-9 y^{2}+7 y-63\)
Multiply: \((3 p q+5)(6 p q-11)\)
Solution
| \((3 p q+5)(6 p q-11)\) | ||
| Multiply the First. | 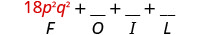 |
 |
| Multiply the Outer. | 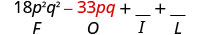 |
|
| Multiply the Inner. | 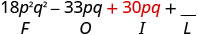 |
|
| Multiply the Last. | 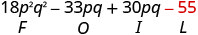 |
|
| Combine like terms—there are none. | \(18 p^{2} q^{2}-3 p q-55\) |
Multiply: \((2 a b+5)(4 a b-4)\)
- Answer
-
\(8 a^{2} b^{2}+12 a b-20\)
Multiply: \((2 x y+3)(4 x y-5)\)
- Answer
-
\(8 x^{2} y^{2}+2 x y-15\)
Multiply a Binomial by a Binomial Using the Vertical Method
The FOIL method is usually the quickest method for multiplying two binomials, but it only works for binomials. You can use the Distributive Property to find the product of any two polynomials. Another method that works for all polynomials is the Vertical Method. It is very much like the method you use to multiply whole numbers. Look carefully at this example of multiplying two-digit numbers.

Now we’ll apply this same method to multiply two binomials.
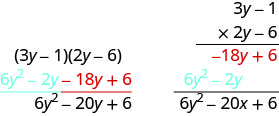
Multiply using the Vertical Method: \((3 y-1)(2 y-6)\)
Solution
It does not matter which binomial goes on the top.
\[\begin{array}{lll}
{\text { Multiply } 3 y-1 \text { by }-6 \text { . }} & & \\
{\text { Multiply } 3 y-1 \text { by } 2 y \text { . }} & & \\
& {\qquad\space3 y-1} & \\
& {\dfrac{ \space\space\times 2 y-6}{\quad-18 y+6}} & \text{partial product} \\
& { {6 y^{2}-2 y} \\ \overline{6 y^{2}-20 y+6} } & \text{partial product} \\
\text{Add like terms.} & & \text{product}
\end{array}\]
Notice the partial products are the same as the terms in the FOIL method.
Multiply using the Vertical Method: \((5 m-7)(3 m-6)\)
- Answer
-
\(15 m^{2}-51 m+42\)
Multiply using the Vertical Method: \((6 b-5)(7 b-3)\)
- Answer
-
\(42 b^{2}-53 b+15\)
We have now used three methods for multiplying binomials. Be sure to practice each method, and try to decide which one you prefer. The methods are listed here all together, to help you remember them.
To multiply binomials, use the:
- Distributive Property
- FOIL Method
- Vertical Method
Remember, FOIL only works when multiplying two binomials.
Multiply a Trinomial by a Binomial
We have multiplied monomials by monomials, monomials by polynomials, and binomials by binomials. Now we’re ready to multiply a trinomial by a binomial. Remember, FOIL will not work in this case, but we can use either the Distributive Property or the Vertical Method. We first look at an example using the Distributive Property.
Multiply using the Distributive Property: \((b+3)\left(2 b^{2}-5 b+8\right)\)
Solution
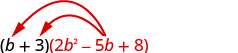 |
|
| Distribute. | 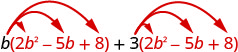 |
| Multiply. | \(2 b^{3}-5 b^{2}+8 b+6 b^{2}-15 b+24\) |
| Combine like terms. | \(2 b^{3}+b^{2}-7 b+24\) |
Multiply using the Distributive Property: \((y-3)\left(y^{2}-5 y+2\right)\)
- Answer
-
\(y^{3}-8 y^{2}+17 y-6\)
Multiply using the Distributive Property: \((x+4)\left(2 x^{2}-3 x+5\right)\)
- Answer
-
\(2 x^{3}+5 x^{2}-7 x+20\)
Now let’s do this same multiplication using the Vertical Method.
Multiply using the Vertical Method: \((b+3)\left(2 b^{2}-5 b+8\right)\)
Solution
It is easier to put the polynomial with fewer terms on the bottom because we get fewer partial products this way.
| Multiply \((2b^2 − 5b + 8)\) by 3. | 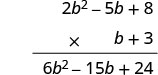 |
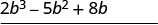 |
|
| Multiply \((2b^2 − 5b + 8)\) by \(b\). | \(2 b^{3}+b^{2}-7 b+24\) |
| Add like terms. |
Multiply using the Vertical Method: \((y-3)\left(y^{2}-5 y+2\right)\)
- Answer
-
\(y^{3}-8 y^{2}+17 y-6\)
Multiply using the Vertical Method: \((x+4)\left(2 x^{2}-3 x+5\right)\)
- Answer
-
\(2 x^{3}+5 x^{2}-7 x+20\)
We have now seen two methods you can use to multiply a trinomial by a binomial. After you practice each method, you’ll probably find you prefer one way over the other. We list both methods are listed here, for easy reference.
To multiply a trinomial by a binomial, use the:
- Distributive Property
- Vertical Method
Access these online resources for additional instruction and practice with multiplying polynomials:
- Multiplying Exponents 1
- Multiplying Exponents 2
- Multiplying Exponents 3
Key Concepts
- FOIL Method for Multiplying Two Binomials—To multiply two binomials:
- Multiply the First terms.
- Multiply the Outer terms.
- Multiply the Inner terms.
- Multiply the Last terms.
- Multiplying Two Binomials—To multiply binomials, use the:
- Multiplying a Trinomial by a Binomial—To multiply a trinomial by a binomial, use the:


