6.3E: Exercises
- Page ID
- 30253
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Practice Makes Perfect
Multiply a Polynomial by a Monomial
In the following exercises, multiply.
4\((w+10)\)
- Answer
-
4w+40
6(b+8)
−3(a+7)
- Answer
-
−3a−21
−5(p+9)
2(x−7)
- Answer
-
2x−14
7(y−4)
−3(k−4)
- Answer
-
−3k+12
−8(j−5)
q(q+5)
- Answer
-
\(q^{2}+5 q\)
k(k+7)
−b(b+9)
- Answer
-
\(-b^{2}-9 b\)
−y(y+3)
−x(x−10)
- Answer
-
\(-x^{2}+10 x\)
−p(p−15)
6r(4r+s)
- Answer
-
\(24 r^{2}+6 r s\)
5c(9c+d)
12x(x−10)
- Answer
-
\(12 x^{2}-120 x\)
9m(m−11)
−9a(3a+5)
- Answer
-
\(-27 a^{2}-45 a\)
−4p(2p+7)
3\(\left(p^{2}+10 p+25\right)\)
- Answer
-
\(3 p^{2}+30 p+75\)
6\(\left(y^{2}+8 y+16\right)\)
\(-8 x\left(x^{2}+2 x-15\right)\)
- Answer
-
\(-8 x^{3}-16 x^{2}+120 x\)
\(-5 t\left(t^{2}+3 t-18\right)\)
5\(q^{3}\left(q^{3}-2 q+6\right)\)
- Answer
-
\(5 q^{6}-10 q^{4}+30 q^{3}\)
4\(x^{3}\left(x^{4}-3 x+7\right)\)
\(-8 y\left(y^{2}+2 y-15\right)\)
- Answer
-
\(-8 y^{3}-16 y^{2}+120 y\)
\(-5 m\left(m^{2}+3 m-18\right)\)
5\(q^{3}\left(q^{2}-2 q+6\right)\)
- Answer
-
\(5 q^{5}-10 q^{4}+30 q^{3}\)
9\(r^{3}\left(r^{2}-3 r+5\right)\)
\(-4 z^{2}\left(3 z^{2}+12 z-1\right)\)
- Answer
-
\(-12 z^{4}-48 z^{3}+4 z^{2}\)
\(-3 x^{2}\left(7 x^{2}+10 x-1\right)\)
\((2 m-9) m\)
- Answer
-
\(2 m^{2}-9 m\)
\((8 j-1) j\)
\((w-6) \cdot 8\)
- Answer
-
\(8 w-48\)
\((k-4) \cdot 5\)
4\((x+10)\)
- Answer
-
4x+40
6(y+8)
15(r−24)
- Answer
-
15r−360
12(v−30)
−3(m+11)
- Answer
-
−3m−33
−4(p+15)
−8(z−5)
- Answer
-
−8z+40
−3(x−9)
u(u+5)
- Answer
-
\(u^{2}+5 u\)
\(q(q+7)\)
\(n\left(n^{2}-3 n\right)\)
- Answer
-
\(n^{3}-3 n^{2}\)
\(s\left(s^{2}-6 s\right)\)
6\(x(4 x+y)\)
- Answer
-
\(24 x^{2}+6 x y\)
5a(9a+b)
5p(11p−5q)
- Answer
-
\(55 p^{2}-25 p q\)
12\(u(3 u-4 v)\)
3\(\left(v^{2}+10 v+25\right)\)
- Answer
-
\(3 v^{2}+30 v+75\)
6\(\left(x^{2}+8 x+16\right)\)
2\(n\left(4 n^{2}-4 n+1\right)\)
- Answer
-
\(8 n^{3}-8 n^{2}+2 n\)
3\(r\left(2 r^{2}-6 r+2\right)\)
\(-8 y\left(y^{2}+2 y-15\right)\)
- Answer
-
\(-8 y^{3}-16 y^{2}+120 y\)
\(-5 m\left(m^{2}+3 m-18\right)\)
5\(q^{3}\left(q^{2}-2 q+6\right)\)
- Answer
-
\(5 q^{5}-10 q^{4}+30 q^{3}\)
9\(r^{3}\left(r^{2}-3 r+5\right)\)
\(-4 z^{2}\left(3 z^{2}+12 z-1\right)\)
- Answer
-
\(-12 z^{4}-48 z^{3}+4 z^{2}\)
\(-3 x^{2}\left(7 x^{2}+10 x-1\right)\)
\((2 y-9) y\)
- Answer
-
\(18 y^{2}-9 y\)
\((8 b-1) b\)
Multiply a Binomial by a Binomial
In the following exercises, multiply the following binomials using: ⓐ the Distributive Property ⓑ the FOIL method ⓒ the Vertical Method.
(w+5)(w+7)
- Answer
-
\(w^{2}+12 w+35\)
(y+9)(y+3)
(p+11)(p−4)
- Answer
-
\(p^{2}+7 p-44\)
(q+4)(q−8)
In the following exercises, multiply the binomials. Use any method.
(x+8)(x+3)
- Answer
-
\(x^{2}+11 x+24\)
(y+7)(y+4)
(y−6)(y−2)
- Answer
-
\(y^{2}-8 y+12\)
(x−7)(x−2)
(w−4)(w+7)
- Answer
-
\(w^{2}+3 w-28\)
\((q-5)(q+8)\)
(p+12)(p−5)
- Answer
-
\(p^{2}+7 p-60\)
(m+11)(m−4)
(6p+5)(p+1)
- Answer
-
\(6 p^{2}+11 p+5\)
\((7 m+1)(m+3)\)
(2t−9)(10t+1)
- Answer
-
\(20 t^{2}-88 t-9\)
(3r−8)(11r+1)
(5x−y)(3x−6)
- Answer
-
\(15 x^{2}-3 x y-30 x+6 y\)
(10a−b)(3a−4)
(a+b)(2a+3b)
- Answer
-
\(2 a^{2}+5 a b+3 b^{2}\)
(r+s)(3r+2s)
(4z−y)(z−6)
- Answer
-
\(4 z^{2}-24 z-z y+6 y\)
(5x−y)(x−4)
\(\left(x^{2}+3\right)(x+2)\)
- Answer
-
\(x^{3}+2 x^{2}+3 x+6\)
\(\left(y^{2}-4\right)(y+3)\)
\(\left(x^{2}+8\right)\left(x^{2}-5\right)\)
- Answer
-
\(x^{4}+3 x^{2}-40\)
\(\left(y^{2}-7\right)\left(y^{2}-4\right)\)
(5ab−1)(2ab+3)
- Answer
-
\(10 a^{2} b^{2}+13 a b-3\)
(2xy+3)(3xy+2)
(6pq−3)(4pq−5)
- Answer
-
\(24 p^{2} q^{2}-42 p q+15\)
(3rs−7)(3rs−4)
Multiply a Trinomial by a Binomial
In the following exercises, multiply using ⓐ the Distributive Property ⓑ the Vertical Method.
\((x+5)\left(x^{2}+4 x+3\right)\)
- Answer
-
\(x^{3}+9 x^{2}+23 x+15\)
\((u+4)\left(u^{2}+3 u+2\right)\)
\((y+8)\left(4 y^{2}+y-7\right)\)
- Answer
-
\(4 y^{3}+33 y^{2}+y-56\)
\((a+10)\left(3 a^{2}+a-5\right)\)
In the following exercises, multiply. Use either method.
\((w-7)\left(w^{2}-9 w+10\right)\)
- Answer
-
\(w^{3}-16 w^{2}+73 w-70\)
\((p-4)\left(p^{2}-6 p+9\right)\)
\((3 q+1)\left(q^{2}-4 q-5\right)\)
- Answer
-
\(3 q^{3}-11 q^{2}-19 q-5\)
\((6 r+1)\left(r^{2}-7 r-9\right)\)
Mixed Practice
(10y−6)+(4y−7)
- Answer
-
14y−13
(15p−4)+(3p−5)
\(\left(x^{2}-4 x-34\right)-\left(x^{2}+7 x-6\right)\)
- Answer
-
−11x−28
\(\left(j^{2}-8 j-27\right)-\left(j^{2}+2 j-12\right)\)
5\(q\left(3 q^{2}-6 q+11\right)\)
- Answer
-
\(15 q^{3}-30 q^{2}+55 q\)
8\(t\left(2 t^{2}-5 t+6\right)\)
(s−7)(s+9)
- Answer
-
\(s^{2}+2 s-63\)
(x−5)(x+13)
\(\left(y^{2}-2 y\right)(y+1)\)
- Answer
-
\(y^{3}-y^{2}-2 y\)
\(\left(a^{2}-3 a\right)(4 a+5)\)
\((3 n-4)\left(n^{2}+n-7\right)\)
- Answer
-
\(3 n^{3}-n^{2}-25 n+28\)
\((6 k-1)\left(k^{2}+2 k-4\right)\)
\((7 p+10)(7 p-10)\)
- Answer
-
\(49 p^{2}-100\)
(3y+8)(3y−8)
\(\left(4 m^{2}-3 m-7\right) m^{2}\)
- Answer
-
\(4 m^{4}-3 m^{3}-7 m^{2}\)
\(\left(15 c^{2}-4 c+5\right) c^{4}\)
\((5 a+7 b)(5 a+7 b)\)
- Answer
-
\(25 a^{2}+70 a b+49 b^{2}\)
(3x−11y)(3x−11y)
(4y+12z)(4y−12z)
- Answer
-
\(16 y^{2}-144 z^{2}\)
Everyday Math
Mental math You can use binomial multiplication to multiply numbers without a calculator. Say you need to multiply 13 times 15. Think of 13 as 10+3 and 15 as 10+5.
- Multiply (10+3)(10+5) by the FOIL method.
- Multiply 13·15 without using a calculator.
- Which way is easier for you? Why?
Mental math You can use binomial multiplication to multiply numbers without a calculator. Say you need to multiply 18 times 17. Think of 18 as 20−2 and 17 as 20−3.
- Multiply (20−2)(20−3) by the FOIL method.
- Multiply 18·17 without using a calculator.
- Which way is easier for you? Why?
- Answer
-
- 306
- 306
- Answers will vary.
Writing Exercises
Which method do you prefer to use when multiplying two binomials: the Distributive Property, the FOIL method, or the Vertical Method? Why?
Which method do you prefer to use when multiplying a trinomial by a binomial: the Distributive Property or the Vertical Method? Why?
- Answer
-
Answers will vary.
Multiply the following:
\(\begin{array}{l}{(x+2)(x-2)} \\ {(y+7)(y-7)} \\ {(w+5)(w-5)}\end{array}\)
Explain the pattern that you see in your answers.
Multiply the following:
\(\begin{array}{l}{(m-3)(m+3)} \\ {(n-10)(n+10)} \\ {(p-8)(p+8)}\end{array}\)
Explain the pattern that you see in your answers.
- Answer
-
Answers may vary.
Multiply the following:
\(\begin{array}{l}{(p+3)(p+3)} \\ {(q+6)(q+6)} \\ {(r+1)(r+1)}\end{array}\)
Explain the pattern that you see in your answers.
Multiply the following:
\(\begin{array}{l}{(x-4)(x-4)} \\ {(y-1)(y-1)} \\ {(z-7)(z-7)}\end{array}\)
Explain the pattern that you see in your answers.
- Answer
-
Answers may vary.
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
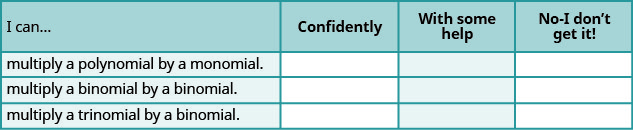
b. What does this checklist tell you about your mastery of this section? What steps will you take to improve?


