6.2: Use Multiplication Properties of Exponents
- Page ID
- 15159
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Simplify expressions with exponents
- Simplify expressions using the Product Property for Exponents
- Simplify expressions using the Power Property for Exponents
- Simplify expressions using the Product to a Power Property
- Simplify expressions by applying several properties
- Multiply monomials
Before you get started, take this readiness quiz.
- Simplify: \(\frac{3}{4}\cdot \frac{3}{4}\)
If you missed this problem, review Example 1.6.13. - Simplify: \((−2)(−2)(−2)\).
If you missed this problem, review Example 1.5.13.
Simplify Expressions with Exponents
Remember that an exponent indicates repeated multiplication of the same quantity. For example, \(2^4\) means the product of \(4\) factors of \(2\), so \(2^4\) means \(2·2·2·2\).
Let’s review the vocabulary for expressions with exponents.
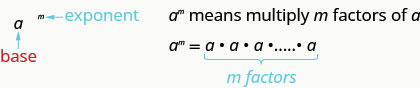
This is read \(a\) to the \(m^{th}\) power.
In the expression \(a^{m}\), the exponent \(m\) tells us how many times we use the base a as a factor.

Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.
Simplify:
- \(4^{3}\)
- \(7^{1}\)
- \(\left(\frac{5}{6}\right)^{2}\)
- \((0.63)^{2}\)
Solution
\(\begin{array}{ll}
\text{a.} && 4^{3}\\
& {\text { Multiply three factors of } 4 .} & {4 \cdot 4 \cdot 4} \\
& {\text { Simplify. }} & {64} \end{array} \)
\(\begin{array}{lll}
\text{b.} && 7^{1}\\
& \text{Multiply one factor of 7.} \quad \; & 7 \end{array} \)
\(\begin{array}{lll}
\text{c.} &&\left(\frac{5}{6}\right)^{2}\\
& {\text { Multiply two factors. }} \quad \quad
& {\left(\frac{5}{6}\right)\left(\frac{5}{6}\right)} \\
& {\text { Simplify. }} & {\frac{25}{36}}\end{array} \)
\(\begin{array}{lll}
\text{d.} &&(0.63)^{2}\\
& {\text { Multiply two factors. }} \quad \quad & {(0.63)(0.63)} \\
& {\text { Simplify. }} & {0.3969} \end{array}\)
Simplify:
- \(6^{3}\)
- \(15^{1}\)
- \(\left(\frac{3}{7}\right)^{2}\)
- \((0.43)^{2}\)
- Answer
-
- 216
- 15
- \(\frac{9}{49}\)
- 0.1849
Simplify:
- \(2^{5}\)
- \(21^{1}\)
- \(\left(\frac{2}{5}\right)^{3}\)
- \((0.218)^{2}\)
- Answer
-
- 32
- 21
- \(\frac{8}{125}\)
- 0.047524
Simplify:
- \((-5)^{4}\)
- \(-5^{4}\)
Solution
- \(\begin{array}{ll} &(-5)^{4}\\{\text { Multiply four factors of }-5} & {(-5)(-5)(-5)} \\ {\text { Simplify. }} & {625}\end{array}\)
- \(\begin{array}{ll} &-5^{4}\\{\text { Multiply four factors of } 5 .} & {-(5 \cdot 5 \cdot 5 \cdot 5)} \\ {\text { Simplify. }} & {-625}\end{array}\)
Notice the similarities and differences in Example \(\PageIndex{4}\) part 1 and Example \(\PageIndex{4}\) part 2! Why are the answers different? As we follow the order of operations in part 1 the parentheses tell us to raise the \((−5)\) to the 4th power. In part 2 we raise just the \(5\) to the 4th power and then take the opposite.
Simplify:
- \((-3)^{4}\)
- \(-3^{4}\)
- Answer
-
- 81
- −81
Simplify:
- \((-13)^{4}\)
- \(-13^{4}\)
- Answer
-
- 169
- −169
Simplify Expressions Using the Product Property for Exponents
You have seen that when you combine like terms by adding and subtracting, you need to have the same base with the same exponent. But when you multiply and divide, the exponents may be different, and sometimes the bases may be different, too.
We’ll derive the properties of exponents by looking for patterns in several examples.
First, we will look at an example that leads to the Product Property.
 |
|
| What does this mean? How many factors altogether? |
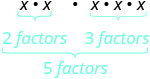 |
| So, we have | \( \qquad \qquad x^{5} \) |
| Notice that 5 is the sum of the exponents, 2 and 3. | \( x^{2} \cdot x^{3} \) is \( x^{2+3} \) or \( x^{5} \) |
We write: \[\begin{array}{c}{x^{2} \cdot x^{3}} \\ {x^{2+3}} \\ {x^{5}}\end{array}\]
The base stayed the same and we added the exponents. This leads to the Product Property for Exponents.
If \(a\) is a real number, and \(m\) and \(n\) are counting numbers, then
\[a^{m} \cdot a^{n}=a^{m+n}\]
To multiply with like bases, add the exponents.
An example with numbers helps to verify this property.
\[\begin{array}{rll} {2^3\cdot2^2} &\stackrel{?}{=} & 2^{2+3}\\ {4\cdot 8} &\stackrel{?}{=} & 2^{5} \\ {32} &=& 32\checkmark\end{array}\]
Simplify: \(y^{5} \cdot y^{6}\)
Solution
| \(y^{5} \cdot y^{6}\) | |
| Use the product property, \(a^{m} \cdot a^{n}=a^{m+n}\). | \( y^ { \color{red}{5+6 }} \) |
| Simplify. | \(y^{11}\) |
Simplify: \(b^{9} \cdot b^{8}\)
- Answer
-
\(b^{17}\)
Simplify: \(x^{12} \cdot x^{4}\)
- Answer
-
\(x^{16}\)
Simplify:
- \(2^{5} \cdot 2^{9}\)
- \(3\cdot 3^{4}\)
Solution
a.
| \(2^{5} \cdot 2^{9}\) | |
| Use the product property, \(a^{m} \cdot a^{n}=a^{m+n}\). | \( 2^ { \color{red}{5+9 }} \) |
| Simplify. | \( 2^{14} \) |
b.
| \(3\cdot 3^{4}\) | |
| Use the product property, \(a^{m} \cdot a^{n}=a^{m+n}\). | \( 3^ { \color{red}{1+4 }} \) |
| Simplify. | \( 3^{5} \) |
Simplify:
- \(5\cdot 5^{5}\)
- \(4^{9} \cdot 4^{9}\)
- Answer
-
- \(5^{6}\)
- \(4^{18}\)
Simplify:
- \(7^{6} \cdot 7^{8}\)
- \(10 \cdot 10^{10}\)
- Answer
-
- \(7^{14}\)
- \(10^{11}\)
Simplify:
- \(a^{7} \cdot a\)
- \(x^{27} \cdot x^{13}\)
Solution
a.
| \(a^{7} \cdot a\) | |
| Rewrite, \(a = a^1\) | \(a^{7} \cdot a^1 \) |
| Use the product property, \(a^m\cdot a^n = a^{m+n}\). | \( a^ { \color{red}{7+1 }} \) |
| Simplify. | \( a^{8} \) |
b.
| \(x^{27} \cdot x^{13}\) | |
| Notice, the bases are the same, so add the exponents. | \( x^ { \color{red}{27+13 }} \) |
| Simplify. | \( x^{40} \) |
Simplify:
- \(p^{5} \cdot p\)
- \(y^{14} \cdot y^{29}\)
- Answer
-
- \(p^{6}\)
- \(y^{43}\)
Simplify:
- \(z \cdot z^{7}\)
- \(b^{15} \cdot b^{34}\)
- Answer
-
- \(z^{8}\)
- \(b^{49}\)
We can extend the Product Property for Exponents to more than two factors.
Simplify: \(d^{4} \cdot d^{5} \cdot d^{2}\)
Solution
| \(d^{4} \cdot d^{5} \cdot d^{2}\) | |
| Add the exponents, since bases are the same. | \( d^ { \color{red}{4+5+2 }} \) |
| Simplify. | \( d^{11} \) |
Simplify: \(x^{6} \cdot x^{4} \cdot x^{8}\)
- Answer
-
\(x^{18}\)
Simplify: \(b^{5} \cdot b^{9} \cdot b^{5}\)
- Answer
-
\(b^{19}\)
Simplify Expressions Using the Power Property for Exponents
Now let’s look at an exponential expression that contains a power raised to a power. See if you can discover a general property.
| \( \qquad \qquad \left( x^{2} \right)^{3} \) | |
| What does this mean? How many factors altogether? |
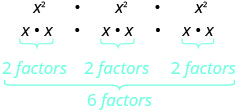 |
| So we have | \( \qquad \qquad x^6 \) |
| Notice that 6 is the product of the exponents, 2 and 3. | \( \left(x^{2}\right)^{3} \) is \( x^{2 \cdot 3 } \) or \( x^6 \) |
We write:
\[\begin{array}{c}{\left(x^{2}\right)^{3}} \\ {x^{2 \cdot 3}} \\ {x^{6}}\end{array}\]
We multiplied the exponents. This leads to the Power Property for Exponents.
If \(a\) is a real number, and \(m\) and \(n\) are whole numbers, then
\[\left(a^{m}\right)^{n}=a^{m \cdot n}\]
To raise a power to a power, multiply the exponents.
An example with numbers helps to verify this property.
\[\begin{array} {lll} \left(3^{2}\right)^{3} &\stackrel{?}{=}&3^{2 \cdot 3} \\(9)^{3} &\stackrel{?}{=} & 3^{6} \\ 729 &=&729\checkmark \end{array}\]
Simplify:
- \(\left(y^{5}\right)^{9}\)
- \(\left(4^{4}\right)^{7}\)
Solution
a.
| \(\left(y^{5}\right)^{9}\) | |
| Use the power property, \(\big(a^m\big)^n = a^{m\cdot n}\). | \( y^ { \color{red}{5 \cdot 9 }} \) |
| Simplify. | \( y^{45} \) |
b.
| \(\left(4^{4}\right)^{7}\) | |
| Use the power property. | \( y^ { \color{red}{4 \cdot 7 }} \) |
| Simplify. | \( 4^{28} \) |
Simplify:
- \( \left(b^{7}\right)^{5} \)
- \(\left(5^{4}\right)^{3}\)
- Answer
-
- \( b^{35}\)
- \(5^{12}\)
Simplify:
- \(\left(z^{6}\right)^{9}\)
- \(\left(3^{7}\right)^{7}\)
- Answer
-
- \(z^{54}\)
- \(3^{49}\)
Simplify Expressions Using the Product to a Power Property
We will now look at an expression containing a product that is raised to a power. Can you find this pattern?
\(\begin{array}{ll}{\text { What does this mean? }} & {(2 x)^{3}} \\ {\text { We group the like factors together. }} & {2 x \cdot 2 x \cdot 2 x} \\ {\text { How many factors of } 2 \text { and of } x ?} & {2 \cdot2 \cdot 2 \cdot x^{3}} \\ {\text { Notice that each factor was raised to the power and }(2 x)^{3} \text { is } 2^{3} \cdot x^{3}}\end{array}\)
\(\begin{array}{ll}\text{We write:} & {(2 x)^{3}} \\ & {2^{3} \cdot x^{3}}\end{array}\)
The exponent applies to each of the factors! This leads to the Product to a Power Property for Exponents.
If \(a\) and \(b\) are real numbers and \(m\) is a whole number, then
\[(a b)^{m}=a^{m} b^{m}\]
To raise a product to a power, raise each factor to that power.
An example with numbers helps to verify this property:
\[\begin{array}{lll}(2 \cdot 3)^{2} &\stackrel{?}{=}&2^{2} \cdot 3^{2} \\ 6^{2} &\stackrel{?}{=}&4 \cdot 9 \\ 36 &=&36
\checkmark \end{array}\]
Simplify:
- \((-9 d)^{2}\)
- \((3mn)^{3}\).
Solution
a.
| \((-9 d)^{2}\) | |
| Use Power of a Product Property, \((ab)^m=a^m b^m\). | \( (-9)^{ \color{red}{2}} d^{ \color{red}{2}} \) |
| Simplify. | \( 81 d^{2} \) |
| \((3mn)^{3}\). | |
| Use Power of a Product Property, \((ab)^m=a^m b^m\). | \( (3)^{ \color{red}{3}} m^{ \color{red}{3}} n^{ \color{red}{3}} \) |
| Simplify. | \( 27 m^{3} n^{3} \) |
Simplify:
- \((-12 y)^{2}\)
- \((2 w x)^{5}\)
- Answer
-
- \(144y^{2}\)
- \(32w^{5} x^{5}\)
Simplify:
- \((5 w x)^{3}\)
- \((-3 y)^{3}\)
- Answer
-
- \(125 w^{3} x^{3}\)
- \(-27 y^{3}\)
Simplify Expressions by Applying Several Properties
We now have three properties for multiplying expressions with exponents. Let’s summarize them and then we’ll do some examples that use more than one of the properties.
If \(a\) and \(b\) are real numbers, and \(m\) and \(n\) are whole numbers, then
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]
All exponent properties hold true for any real numbers \(m\) and \(n\). Right now, we only use whole number exponents.
Simplify:
- \(\left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\)
- \(\left(-6 x^{4} y^{5}\right)^{2}\)
Solution
\(\begin{array}{lll}
\text{a.} && \left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\\
& {\text { Use the Power Property. }}& y^{18} \cdot y^{20} \\
& {\text { Add the exponents. }} & y^{38} \end{array}\)
\(\begin{array}{lll}
\text{b.} && \left(-6 x^{4} y^{5}\right)^{2}\\
& {\text { Use the Product to a Power Property. }} & {(-6)^{2}\left(x^{4}\right)^{2}\left(y^{5}\right)^{2}} \\
& {\text { Use the Power Property. }} & {(-6)^{2}\left(x^{8}\right)\left(y^{10}\right)^{2}} \\
& {\text { Simplify. }} & {36 x^{8} y^{10}}\end{array}\)
Simplify:
- \(\left(a^{4}\right)^{5}\left(a^{7}\right)^{4}\)
- \(\left(-2 c^{4} d^{2}\right)^{3}\)
- Answer
-
- \(a^{48}\)
- \(-8 c^{12} d^{6}\)
Simplify:
- \(\left(-3 x^{6} y^{7}\right)^{4}\)
- \(\left(q^{4}\right)^{5}\left(q^{3}\right)^{3}\)
- Answer
-
- \( 81 x^{24} y^{28}\)
- \(q^{29}\)
Simplify:
- \((5 m)^{2}\left(3 m^{3}\right)\)
- \(\left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3}\)
Solution
- \(\begin{array}{ll}& (5 m)^{2}\left(3 m^{3}\right)\\{\text { Raise } 5 m \text { to the second power. }} & {5^{2} m^{2} \cdot 3 m^{3}} \\ {\text { Simplify. }} & {25 m^{2} \cdot 3 m^{3}} \\ {\text { Use the Commutative Property. }} & {25 \cdot 3 \cdot m^{2} \cdot m^{3}} \\ {\text { Multiply the constants and add the exponents. }} & {75 m^{5}}\end{array}\)
- \(\begin{array}{ll} & \left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3} \\ \text{Use the Product to a Power Property.} & \left(3^{4} x^{8} y^{4}\right)\left(2^{3} x^{3} y^{6}\right)\\\text{Simplify.} & \left(81 x^{8} y^{4}\right)\left(8 x^{3} y^{6}\right)\\ \text{Use the Commutative Property.} &81\cdot 8 \cdot x^{8} \cdot x^{3} \cdot y^{4} \cdot y^{6} \\\text{Multiply the constants and add the exponents.} & 648x^{11} y^{10}\\ \end{array}\)
Simplify:
- \((5 n)^{2}\left(3 n^{10}\right)\)
- \(\left(c^{4} d^{2}\right)^{5}\left(3 c d^{5}\right)^{4}\)
- Answer
-
- \( 75 n^{12}\)
- \( 81 c^{24} d^{30}\)
Simplify:
- \(\left(a^{3} b^{2}\right)^{6}\left(4 a b^{3}\right)^{4}\)
- \((2 x)^{3}\left(5 x^{7}\right)\)
- Answer
-
- \( 256 a^{22} b^{24}\)
- \( 40 x^{10}\)
Multiply Monomials
Since a monomial is an algebraic expression, we can use the properties of exponents to multiply monomials.
Multiply: \(\left(3 x^{2}\right)\left(-4 x^{3}\right)\)
Solution
\(\begin{array}{ll} & \left(3 x^{2}\right)\left(-4 x^{3}\right)\\ \text{Use the Commutative Property to rearrange the terms.} & 3\cdot(-4) \cdot x^{2} \cdot x^{3}\\
\text{Multiply.} & -12 x^{5}\end{array}\)
Multiply: \(\left(5 y^{7}\right)\left(-7 y^{4}\right)\)
- Answer
-
\(-35 y^{11}\)
Multiply: \(\left(-6 b^{4}\right)\left(-9 b^{5}\right)\)
- Answer
-
\( 54 b^{9}\)
Multiply: \(\left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\)
Solution
\(\begin{array}{ll} & \left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\\ \text{Use the Commutative Property to rearrange the terms.} & \frac{5}{6} \cdot 12 \cdot x^{3} \cdot x \cdot y \cdot y^{2}\\ \text{Multiply.} &10x^{4} y^{3}\end{array}\)
Multiply: \(\left(\frac{2}{5} a^{4} b^{3}\right)\left(15 a b^{3}\right)\)
- Answer
-
\( 6 a^{5} b^{6}\)
Multiply: \(\left(\frac{2}{3} r^{5} s\right)\left(12 r^{6} s^{7}\right)\)
- Answer
-
\( 8 r^{11} s^{8}\)
Access these online resources for additional instruction and practice with using multiplication properties of exponents:
- Multiplication Properties of Exponents
Key Concepts
- Exponential Notation
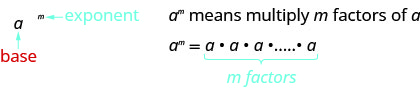
- Properties of Exponents
- If \(a\) and \(b\) are real numbers and \(m\) and \(n\) are whole numbers, then
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]


