7.6: Quadratic Equations
- Page ID
- 15171
By the end of this section, you will be able to:
- Solve quadratic equations by using the Zero Product Property
- Solve quadratic equations factoring
- Solve applications modeled by quadratic equations
Before you get started, take this readiness quiz.
- Solve: \(5y−3=0\).
If you missed this problem, review Example 2.3.1. - Solve: \(10a=0\).
If you missed this problem, review Example 2.2.1. - Combine like terms: \(12 x^{2}-6 x+4 x\).
If you missed this problem, review Example 1.3.37. - Factor \(n^{3}-9 n^{2}-22 n\) completely.
If you missed this problem, review Example 7.3.10.
We have already solved linear equations, equations of the form \(a x+b y=c\). In linear equations, the variables have no exponents. Quadratic equations are equations in which the variable is squared. Listed below are some examples of quadratic equations:
\[x^{2}+5 x+6=0 \quad 3 y^{2}+4 y=10 \quad 64 u^{2}-81=0 \quad n(n+1)=42\]
The last equation doesn’t appear to have the variable squared, but when we simplify the expression on the left we will get \(n^{2}+n\).
The general form of a quadratic equation is \(a x^{2}+b x+c=0\),with \(a \neq 0\).
An equation of the form \(a x^{2}+b x+c=0\) is called a quadratic equation.
\[a, b, \text { and } c \text { are real numbers and } a \neq 0\]
To solve quadratic equations we need methods different than the ones we used in solving linear equations. We will look at one method here and then several others in a later chapter.
Solve Quadratic Equations Using the Zero Product Property
We will first solve some quadratic equations by using the Zero Product Property. The Zero Product Property says that if the product of two quantities is zero, it must be that at least one of the quantities is zero. The only way to get a product equal to zero is to multiply by zero itself.
\(\text { If } a \cdot b=0, \text { then either } a=0 \text { or } b=0 \text { or both. }\)
We will now use the Zero Product Property, to solve a quadratic equation.
Solve: \((x+1)(x-4)=0\)
Solution



Solve: \((x-3)(x+5)=0\)
- Answer
-
\(x=3, x=-5\)
Solve: \((y-6)(y+9)=0\)
- Answer
-
\(y=6, y=-9\)
We usually will do a little more work than we did in this last example to solve the linear equations that result from using the Zero Product Property.
Solve: \((5 n-2)(6 n-1)=0\)
Solution
| \((5 n-2)(6 n-1)=0\) | ||
| Use the Zero Product Property to set each factor to 0. |
\(5 n-2=0 \) |
\(6 n-1=0\) |
| Solve the equations. | \(n=\frac{2}{5}\) | \(n = \frac{1}{6}\) |
| Check your answers. | ||
 |
||
Solve: \((3 m-2)(2 m+1)=0\)
- Answer
-
\(m=\frac{2}{3}, m=-\frac{1}{2}\)
Solve: \((4 p+3)(4 p-3)=0\)
- Answer
-
\(p=-\frac{3}{4}, p=\frac{3}{4}\)
Notice when we checked the solutions that each of them made just one factor equal to zero. But the product was zero for both solutions.
Solve: \(3 p(10 p+7)=0\)
Solution
| \(3p(10p+7)=0\) | ||
| Use the Zero Product Property to set each factor to 0. |
3p=0 | 10p+7=0 |
| Solve the equations. | p=0 | 10p=−7 |
| \(p=-\frac{7}{10}\) | ||
| Check your answers. | ||
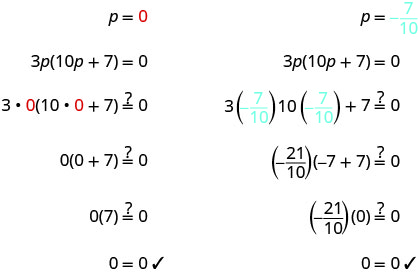 |
||
Solve: \(2 u(5 u-1)=0\)
- Answer
-
\(u=0, u=\frac{1}{5}\)
Solve: \(w(2 w+3)=0\)
- Answer
-
\(w=0, w=-\frac{3}{2}\)
It may appear that there is only one factor in the next example. Remember, however, that \((y-8)^{2}\) means \((y-8)(y-8)\).
Solve: \((y-8)^{2}=0\)
Solution
| \((y−8)^{2}=0\) | ||
| Rewrite the left side as a product. | (y−8)(y−8)=0 | |
| Use the Zero Product Property and set each factor to 0. |
y−8=0 | y−8=0 |
| Solve the equations. | y=8 | y=8 |
| When a solution repeats, we call it a double root. |
||
| Check your answer. | ||
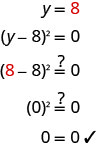 |
||
Solve: \((x+1)^{2}=0\)
- Answer
-
\(x=1\)
Solve: \((v-2)^{2}=0\)
- Answer
-
\(v=2\)
Solve Quadratic Equations by Factoring
Each of the equations we have solved in this section so far had one side in factored form. In order to use the Zero Product Property, the quadratic equation must be factored, with zero on one side. So we be sure to start with the quadratic equation in standard form, \(a x^{2}+b x+c=0\). Then we factor the expression on the left.
Solve: \(x^{2}+2 x-8=0\)
Solution

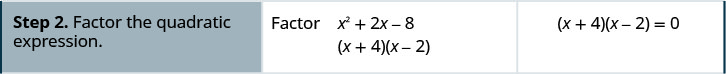



Solve: \(x^{2}-x-12=0\)
- Answer
-
\(x=4, x=-3\)
Solve: \(b^{2}+9 b+14=0\)
- Answer
-
\(b=-2, b=-7\)
- Write the quadratic equation in standard form, \(a x^{2}+b x+c=0\).
- Factor the quadratic expression.
- Use the Zero Product Property.
- Solve the linear equations.
- Check.
Before we factor, we must make sure the quadratic equation is in standard form.
Solve: \(2 y^{2}=13 y+45\)
Solution
| \(2 y^{2}=13 y+45\) | ||
| Write the quadratic equation in standard form. | \(2 y^{2}-13 y-45=0\) | |
| Factor the quadratic expression. | \((2 y+5)(y-9)=0\) | |
| Use the Zero Product Property to set each factor to 0. |
\(2 y+5=0\) | \(y-9=0\) |
| Solve each equation. | \(y=-\frac{5}{2}\) | \(y=9\) |
| Check your answers. | ||
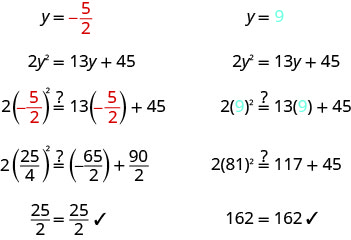 |
Solve: \(3 c^{2}=10 c-8\)
- Answer
-
\(c=0, c=\frac{4}{3}\)
Solve: \(2 d^{2}-5 d=3\)
- Answer
-
\(d=3, d=-\frac{1}{2}\)
Solve: \(5 x^{2}-13 x=7 x\)
Solution
| \(5 x^{2}-13 x=7 x\) | ||
| Write the quadratic equation in standard form. | \(5 x^{2}-20 x=0\) | |
| Factor the left side of the equation. | \(5 x(x-4)=0\) | |
| Use the Zero Product Property to set each factor to 0. |
\(5x=0\) | \(x−4=0\) |
| Solve each equation. | \(x=0\) | \(x=4\) |
| Check your answers. | ||
 |
Solve: \(6 a^{2}+9 a=3 a\)
- Answer
-
\(a=0, a=-1\)
Solve: \(45 b^{2}-2 b=-17 b\)
- Answer
-
\(b=0, b=-\frac{1}{3}\)
Solving quadratic equations by factoring will make use of all the factoring techniques you have learned in this chapter! Do you recognize the special product pattern in the next example?
Solve: \(144 q^{2}=25\)
Solution
\(\begin{array}{lrllrl} & 144 q^{2}&=&25 \\ \text { Write the quadratic equation in standard form. }& 144 q^{2}-25&=& 0 \\ \text { Factor. It is a difference of squares. } & (12 q-5)(12 q+5) & = & 0 \\ \text { Use the Zero Product Property to set each factor to } 0 . & 12 q-5&=&0 & 12 q+5&=&0 \\\text { Solve each equation. } & 12 q & = & 5 & 12 q&=&-5 \\ & q&=&\frac{5}{12} & q & =&-\frac{5}{12} \\ \text { Check your answers. }\end{array}\)
Solve: \(25 p^{2}=49\)
- Answer
-
\(p=\frac{7}{5}, p=-\frac{7}{5}\)
Solve: \(36 x^{2}=121\)
- Answer
-
\(x=\frac{11}{6}, x=-\frac{11}{6}\)
The left side in the next example is factored, but the right side is not zero. In order to use the Zero Product Property, one side of the equation must be zero. We’ll multiply the factors and then write the equation in standard form.
Solve: \((3 x-8)(x-1)=3 x\)
Solution
\(\begin{array}{ll} & (3 x-8)(x-1)=3 x \\ \text { Multiply the binomials. }& 3 x^{2}-11 x+8=3 x \\ \text { Write the quadratic equation in standard form. }& 3 x^{2}-14 x+8=0\\ \text { Factor the trinomial. }& (3 x-2)(x-4)=0\\\text { Use the Zero Product Property to set each factor to } 0 . & 3 x-2=0 \quad x-4=0 \\ \text { Solve each equation. } & 3 x=2 \quad x=4 \\ & x=\frac{2}{3} \\ \text { Check your answers. } & \text {The check is left to you! } \end{array}\)
Solve: \((2 m+1)(m+3)=12 m\)
- Answer
-
\(m=1, m=\frac{3}{2}\)
Solve: \((k+1)(k-1)=8\)
- Answer
-
\(k=3, k=-3\)
The Zero Product Property also applies to the product of three or more factors. If the product is zero, at least one of the factors must be zero. We can solve some equations of degree more than two by using the Zero Product Property, just like we solved quadratic equations.
Solve: \(9 m^{3}+100 m=60 m^{2}\)
Solution
\(\begin{array}{lrllrl} & 9 m^{3}+100 m&=&60 m^{2}\\ \text { Bring all the terms to one side so that the other side is zero. } & 9 m^{3}-60 m^{2}+100 m&=&0 \\ \text { Factor the greatest common factor first. } & m\left(9 m^{2}-60 m+100\right)&=&0 \\ \text { Factor the trinomial. } & m(3 m-10)(3 m-10)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & m&=&0 & 3 m-10&=&0 & 3 m-10&=&0 \\ \text { Solve each equation. } & m&=&0 & m&=&\frac{10}{3}& m&=&\frac{10}{3} \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Solve: \(8 x^{3}=24 x^{2}-18 x\)
- Answer
-
\(x=0, x=\frac{3}{2}\)
Solve: \(16 y^{2}=32 y^{3}+2 y\)
- Answer
-
\(y=0, y=\frac{1}{4}\)
When we factor the quadratic equation in the next example we will get three factors. However the first factor is a constant. We know that factor cannot equal 0.
Solve: \(4 x^{2}=16 x+84\)
Solution
\(\begin{array}{lrllrl} & 4 x^{2}&=&16 x+84\\ \text { Write the quadratic equation in standard form. }& 4 x^{2}-16 x-84&=&0 \\ \text { Factor the greatest common factor first. }& 4\left(x^{2}-4 x-21\right)&=&0 \\ \text { Factor the trinomial. } & 4(x-7)(x+3)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & 4&\neq&0 & x-7&=&0 & x +3&=&0 \\ \text { Solve each equation. } & 4&\neq&0 & x&=&7& x&=&-3 \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Solve: \(18 a^{2}-30=-33 a\)
- Answer
-
\(a=-\frac{5}{2}, a=\frac{2}{3}\)
Solve: \(123 b=-6-60 b^{2}\)
- Answer
-
\(b=2, b=\frac{1}{20}\)
Solve Applications Modeled by Quadratic Equations
The problem solving strategy we used earlier for applications that translate to linear equations will work just as well for applications that translate to quadratic equations. We will copy the problem solving strategy here so we can use it for reference.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
We will start with a number problem to get practice translating words into a quadratic equation.
The product of two consecutive integers is \(132 .\) Find the integers.
Solution
\(\begin{array}{ll} \textbf { Step 1. Read} \text { the problem. } \\ \textbf { Step 2. Identify} \text { what we are looking for. } & \text { We are looking for two consecutive integers. } \\ \textbf { Step 3. Name} \text{ what we are looking for. } & \begin{array}{l}{\text { Let } n=\text { the first integer }} \\ {\space n+1=\text { the next consecutive integer }}\end{array} \\\textbf { Step 4. Translate} \text { into an equation. Restate the } & \text { The product of the two consecutive integers is } 132 . \\ \text { problem in a sentence. } \\ \text { Translate to an equation. } & \begin{array}{c}{\text { The first integer times the next integer is } 132 .} \\ {n(n+1)=132}\end{array} \\ \textbf { Step 5. Solve}\text { the equation. } & n^{2}+n=132 \\ \text { Bring all the terms to one side. } & n^{2}+n-132=0 \\ \text { Factor the trinomial. } & (n-11)(n+12)=0 \\ \text { Use the zero product property. } & n-11=0 \quad n+12=0 \\ \text { Solve the equations. } & n=11 \quad n=-12 \end{array}\)
The product of two consecutive integers is \(240 .\) Find the integers.
- Answer
-
\(-15,-16\) and \(15,16\)
The product of two consecutive integers is \(420 .\) Find the integers.
- Answer
-
\(-21,-20\) and \(20,21\)
Were you surprised by the pair of negative integers that is one of the solutions to the previous example? The product of the two positive integers and the product of the two negative integers both give 132.
In some applications, negative solutions will result from the algebra, but will not be realistic for the situation.
A rectangular garden has an area of 15 square feet. The length of the garden is two feet more than the width. Find the length and width of the garden.
Solution
| Step 1. Read the problem. In problems involving geometric figures, a sketch can help you visualize the situation. |  |
|
| Step 2. Identify what you are looking for. | We are looking for the length and width. | |
| Step 3. Name what you are looking for. The length is two feet more than width. |
Let W = the width of the garden. W + 2 = the length of the garden |
|
| Step 4. Translate into an equation. Restate the important information in a sentence. |
The area of the rectangular garden is 15 square feet. |
|
| Use the formula for the area of a rectangle. | \(A=L \cdot W\) | |
| Substitute in the variables. | \(15=(W+2) W\) | |
| Step 5. Solve the equation. Distribute first. | \(15=W^{2}+2 W\) | |
| Get zero on one side. | \(0=W^{2}+2 W-15\) | |
| Factor the trinomial. | \(0=(W+5)(W-3)\) | |
| Use the Zero Product Property. | \(0=W+5\) | \(0=W−3\) |
| Solve each equation. | \(−5=W\) | \(3=W\) |
| Since W is the width of the garden, it does not make sense for it to be negative. We eliminate that value for W. |
\(W=−5\) cannot be the width, since it's negative. \(W=3\) |
\(3=W\) Width is 3 feet. |
| Find the value of the length. | \(\text{length}=W+2\) | |
| \(\text{length}=3+2\) | ||
| \(\text{length}=5\) | Length is 5 feet. | |
| Step 6. Check the answer. Does the answer make sense? |
||
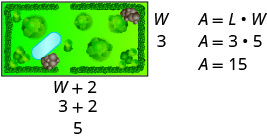 |
||
| Yes, this makes sense. | ||
| Step 7. Answer the question. | The width of the garden is 3 feet and the length is 5 feet. |
|
A rectangular sign has an area of 30 square feet. The length of the sign is one foot more than the width. Find the length and width of the sign.
- Answer
-
55 feet and 66 feet
A rectangular patio has an area of 180 square feet. The width of the patio is three feet less than the length. Find the length and width of the patio.
- Answer
-
12 feet and 15 feet
In an earlier chapter, we used the Pythagorean Theorem \(\left(a^{2}+b^{2}=c^{2}\right)\). It gave the relation between the legs and the hypotenuse of a right triangle.
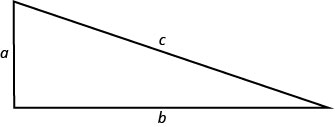
We will use this formula to in the next example.
Justine wants to put a deck in the corner of her backyard in the shape of a right triangle, as shown below. The hypotenuse will be 17 feet long. The length of one side will be 7 feet less than the length of the other side. Find the lengths of the sides of the deck.
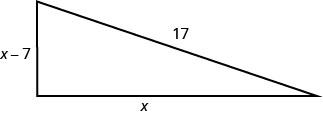
Solution
| Step 1. Read the problem. | |||
| Step 2. Identify what you are looking for. | We are looking for the lengths of the sides of the deck. |
||
| Step 3. Name what you are looking for. One side is 7 less than the other. |
Let x = length of a side of the deck x − 7 = length of other side |
||
| Step 4. Translate into an equation. Since this is a right triangle we can use the Pythagorean Theorem. |
\(a^{2}+b^{2}=c^{2}\) | ||
| Substitute in the variables. | \(x^{2}+(x-7)^{2}=17^{2}\) | ||
| Step 5. Solve the equation. | \(x^{2}+x^{2}-14 x+49=289\) | ||
| Simplify. | \(2 x^{2}-14 x+49=289\) | ||
| It is a quadratic equation, so get zero on one side. | \(2 x^{2}-14 x-240=0\) | ||
| Factor the greatest common factor. | \(2\left(x^{2}-7 x-120\right)=0\) | ||
| Factor the trinomial. | \(2(x-15)(x+8)=0\) | ||
| Use the Zero Product Property. | \(2\neq 0\) | \(x−15=0\) | \(x+8=0\) |
| Solve. | \(2\neq 0\) | \(x=15\) | \(x=-8\) |
| Since \(x\) is a side of the triangle, \(x=−8\) does not make sense. |
\(2\neq 0\) | \(x=15\) | \(\cancel{x=−8}\) |
| Find the length of the other side. | |||
| If the length of one side is | \(x=15\) | ||
| then the length of the other side is | \(x-7\) | ||
| \(15 - 7 = 8\) | |||
| 8 is the length of the other side. | |||
| Step 6. Check the answer. Do these numbers make sense? |
|||
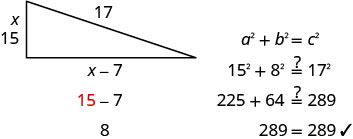 |
|||
| Step 7. Answer the question. | The sides of the deck are 8, 15, and 17 feet. | ||
A boat’s sail is a right triangle. The length of one side of the sail is 7 feet more than the other side. The hypotenuse is 13. Find the lengths of the two sides of the sail.
- Answer
-
5 feet and 12 feet
A meditation garden is in the shape of a right triangle, with one leg 7 feet. The length of the hypotenuse is one more than the length of one of the other legs. Find the lengths of the hypotenuse and the other leg.
- Answer
-
24 feet and 25 feet
Key Concepts
- Zero Product Property If \(a \cdot b=0\), then either a=0 or b=0 or both. See Example.
- Solve a quadratic equation by factoring To solve a quadratic equation by factoring: See Example.
- Write the quadratic equation in standard form, \(a x^{2}+b x+c=0\).
- Factor the quadratic expression.
- Use the Zero Product Property.
- Solve the linear equations.
- Check.
- Use a problem solving strategy to solve word problems See Example.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Glossary
- quadratic equations
- are equations in which the variable is squared.
- Zero Product Property
- The Zero Product Property states that, if the product of two quantities is zero, at least one of the quantities is zero.


