7.3: Factor Quadratic Trinomials with Leading Coefficient Other than 1
- Page ID
- 15168
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Recognize a preliminary strategy to factor polynomials completely
- Factor trinomials of the form \(ax^{2}+bx+c\) with a GCF
- Factor trinomials using trial and error
- Factor trinomials using the ‘ac’ method
Before you get started, take this readiness quiz.
- Find the GCF of 45\(p^{2}\) and 30\(p^{6}\)
If you missed this problem, review Example 7.1.4. - Multiply \((3 y+4)(2 y+5)\)
If you missed this problem, review Example 6.3.37. - Combine like terms \(12 x^{2}+3 x+5 x+9\)
If you missed this problem, review Example 1.3.37.
Recognize a Preliminary Strategy for Factoring
Let’s summarize where we are so far with factoring polynomials. In the first two sections of this chapter, we used three methods of factoring: factoring the GCF, factoring by grouping, and factoring a trinomial by “undoing” FOIL. More methods will follow as you continue in this chapter, as well as later in your studies of algebra.
How will you know when to use each factoring method? As you learn more methods of factoring, how will you know when to apply each method and not get them confused? It will help to organize the factoring methods into a strategy that can guide you to use the correct method.
As you start to factor a polynomial, always ask first, “Is there a greatest common factor?” If there is, factor it first.
The next thing to consider is the type of polynomial. How many terms does it have? Is it a binomial? A trinomial? Or does it have more than three terms?
- If it is a trinomial where the leading coefficient is one, \(x^{2}+b x+c\), use the “undo FOIL” method.
- If it has more than three terms, try the grouping method. This is the only method to use for polynomials of more than three terms.
Some polynomials cannot be factored. They are called “prime.” Below we summarize the methods we have so far.
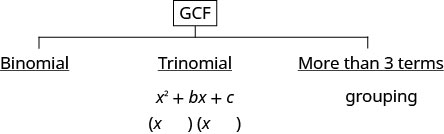
- Is there a greatest common factor?
- Factor it out.
- Is the polynomial a binomial, trinomial, or are there more than three terms?
- If it is a binomial, right now we have no method to factor it.
- If it is a trinomial of the form \(x^{2}+b x+c\): Undo FOIL \((x\qquad)(x\qquad)\)
- If it has more than three terms: Use the grouping method.
- Check by multiplying the factors.
Use the preliminary strategy to completely factor a polynomial. A polynomial is factored completely if, other than monomials, all of its factors are prime.
Identify the best method to use to factor each polynomial.
- \(6 y^{2}-72\)
- \(r^{2}-10 r-24\)
- \(p^{2}+5 p+p q+5 q\)
Answer a
\[\begin{array}{ll} &6 y^{2}-72\\ \text { Is there a greatest common factor? } & \text {Yes, 6. } \\ \text { Factor out the } 6 &6\left(y^{2}-12\right) \\ \text { Is it a binomial, trinomial, or are there } & \text {Binomial, we have no method to factor } \\ \text { more than } 3 \text { terms? } & \text {binomials yet. } \end{array} \nonumber\]
Answer b
\[\begin{array}{ll} &r^{2}-10 r-24\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {Trinomial, with leading coefficient } 1, \text { so } \\ \text { more than three terms? }& \text {"undo" FOIL. }\end{array} \nonumber\]
Answer c
\[\begin{array}{ll} &p^{2}+5 p+p q+5 q\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {More than three terms, so factor using }\\ \text { more than three terms? }& \text {grouping. }\end{array} \nonumber\]
Identify the best method to use to factor each polynomial:
- \(4 y^{2}+32\)
- \(y^{2}+10 y+21\)
- \(y z+2 y+3 z+6\)
- Answer a
-
no method
- Answer b
-
undo using FOIL
- Answer c
-
factor with grouping
Identify the best method to use to factor each polynomial:
- \(a b+a+4 b+4\)
- \(3 k^{2}+15\)
- \(p^{2}+9 p+8\)
- Answer a
-
factor using grouping
- Answer b
-
no method
- Answer c
-
undo using FOIL
Factor Trinomials of the form ax2 + bx + c with a GCF
Now that we have organized what we’ve covered so far, we are ready to factor trinomials whose leading coefficient is not 1, trinomials of the form \(a x^{2}+b x+c\). Remember to always check for a GCF first! Sometimes, after you factor the GCF, the leading coefficient of the trinomial becomes 1 and you can factor it by the methods in the last section. Let’s do a few examples to see how this works. Watch out for the signs in the next two examples.
Factor completely: \(2 n^{2}-8 n-42\).
Solution
Use the preliminary strategy.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&2 n^{2}-8 n-42\\ \text { Yes, GCF }=2 . \text { Factor it out. }& 2\left(n^{2}-4 n-21\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 2(n\qquad )(n\qquad) \\ \text { Use } 3 \text { and }-7 \text { as the last terms of the binomials. } & 2(n+3)(n-7) \end{array}\)
| Factors of −21 | Sum of factors |
|---|---|
| 1,−21 | 1+(−21)=−20 |
| 3,−7 | 3+(−7)=−4* |
\(\begin{array}{l}{\text {Check. }} \\ {2(n+3)(n-7)} \\ {2\left(n^{2}-7 n+3 n-21\right)} \\ {2\left(n^{2}-4 n-21\right)} \\ {2 n^{2}-8 n-42 }\checkmark \end{array}\)
Factor completely: \(4 m^{2}-4 m-8\)
- Answer
-
4\((m+1)(m-2)\)
Factor completely: \(5 k^{2}-15 k-50\)
- Answer
-
5\((k+2)(k-5)\)
Factor completely: \(4 y^{2}-36 y+56\)
Solution
Use the preliminary strategy.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&4 y^{2}-36 y+56\\ \text { Yes, GCF }=4 . \text { Factor it out. }&4\left(y^{2}-9 y+14\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 4(y\qquad )(y\qquad) \\\text { Use a table like the one below to find two numbers that multiply to }&\\ 14 \text { and add to }-9\\ \text { Both factors of } 14 \text { must be negative. } & 4(y-2)(y-7) \end{array}\)
| Factors of 14 | Sum of factors |
|---|---|
| −1,−14 | −1+(−14)=−15 |
| −2,−7 | −2+(−7)=−9* |
\(\begin{array}{l}{\text { Check. }} \\ {4(y-2)(y-7)} \\ {4\left(y^{2}-7 y-2 y+14\right)} \\ {4\left(y^{2}-9 y+14\right)} \\ {4 y^{2}-36 y+42 } \checkmark \end{array}\)
Factor completely: \(3 r^{2}-9 r+6\)
- Answer
-
3\((r-1)(r-2)\)
Factor completely: \(2 t^{2}-10 t+12\)
- Answer
-
2\((t-2)(t-3)\)
In the next example the GCF will include a variable.
Factor completely: \(4 u^{3}+16 u^{2}-20 u\)
Solution
Use the preliminary strategy.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&4 u^{3}+16 u^{2}-20 u\\ \text { Yes, GCF }=4 u . \text { Factor it. }&4 u\left(u^{2}+4 u-5\right) \\\text { Binomial, trinomial, or more than three terms? }&\\ \text { more than three terms? }& \\ \text { It is a trinomial. So "undo FOIL." } & 4u(u\qquad )(u\qquad) \\\text { Use a table like the table below to find two numbers that }&4 u(u-1)(u+5)\\ \text { multiply to }-5 \text { and add to } 4\end{array}\)
| Factors of −5 | Sum of factors |
|---|---|
| −1,5 | −1+5=4* |
| 1,−5 | 1+(−5)=−4 |
Check.
\(\begin{array}{l}{4 u(u-1)(u+5)} \\ {4 u\left(u^{2}+5 u-u-5\right)} \\ {4 u\left(u^{2}+4 u-5\right)} \\ {4 u^{3}+16 u^{2}-20 u }\checkmark \end{array}\)
Factor completely: \(5 x^{3}+15 x^{2}-20 x\)
- Answer
-
5\(x(x-1)(x+4)\)
Factor completely: \(6 y^{3}+18 y^{2}-60 y\)
- Answer
-
6\(y(y-2)(y+5)\)
Factor Trinomials using Trial and Error
What happens when the leading coefficient is not 1 and there is no GCF? There are several methods that can be used to factor these trinomials. First we will use the Trial and Error method.
Let’s factor the trinomial \(3 x^{2}+5 x+2\)
From our earlier work we expect this will factor into two binomials.
\[\begin{array}{c}{3 x^{2}+5 x+2} \\ {( \qquad)( \qquad)}\end{array}\]
We know the first terms of the binomial factors will multiply to give us 3\(x^{2}\). The only factors of 3\(x^{2}\) are \(1 x, 3 x\). We can place them in the binomials.
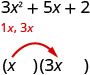
Check. Does \(1 x \cdot 3 x=3 x^{2}\)?
We know the last terms of the binomials will multiply to 2. Since this trinomial has all positive terms, we only need to consider positive factors. The only factors of 2 are 1 and 2. But we now have two cases to consider as it will make a difference if we write 1, 2, or 2, 1.

Which factors are correct? To decide that, we multiply the inner and outer terms.
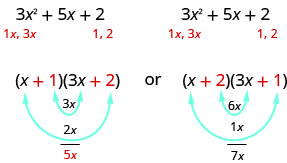
Since the middle term of the trinomial is 5x, the factors in the first case will work. Let’s FOIL to check.
\[\begin{array}{l}{(x+1)(3 x+2)} \\ {3 x^{2}+2 x+3 x+2} \\ {3 x^{2}+5 x+2}\checkmark \end{array}\]
Our result of the factoring is:
\[\begin{array}{l}{3 x^{2}+5 x+2} \\ {(x+1)(3 x+2)}\end{array}\]
Factor completely: \(3 y^{2}+22 y+7\)
Solution





Factor completely: \(2 a^{2}+5 a+3\)
- Answer
-
\((a+1)(2 a+3)\)
Factor completely: \(4 b^{2}+5 b+1\)
- Answer
-
\((b+1)(4 b+1)\)
- Write the trinomial in descending order of degrees.
- Find all the factor pairs of the first term.
- Find all the factor pairs of the third term.
- Test all the possible combinations of the factors until the correct product is found.
- Check by multiplying.
When the middle term is negative and the last term is positive, the signs in the binomials must both be negative.
Factor completely: \(6 b^{2}-13 b+5\)
Solution
| The trinomial is already in descending order. | 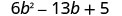 |
| Find the factors of the first term. | 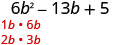 |
| Find the factors of the last term. Consider the signs. Since the last term, 5 is positive its factors must both be positive or both be negative. The coefficient of the middle term is negative, so we use the negative factors. | 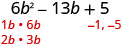 |
| \(6 b^{2}-13 b+5\) | |
|---|---|
| Possible factors | Product |
| (b−1)(6b−5) | \(6 b^{2}-11 b+5\) |
| (b−5)(6b−1) | \(6 b^{2}-31 b+5\) |
| (2b−1)(3b−5) | \(6 b^{2}-13 b+5\) * |
| (2b−5)(3b−1) | \(6 b^{2}-17 b+5\) |
Factor completely: \(8 x^{2}-14 x+3\)
- Answer
-
\((2 x-3)(4 x-1)\)
Factor completely: \(10 y^{2}-37 y+7\)
- Answer
-
\((2 y-7)(5 y-1)\)
When we factor an expression, we always look for a greatest common factor first. If the expression does not have a greatest common factor, there cannot be one in its factors either. This may help us eliminate some of the possible factor combinations.
Factor completely: \(14 x^{2}-47 x-7\)
Solution
| The trinomial is already in descending order. | 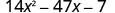 |
| Find the factors of the first term. | 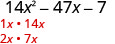 |
| Find the factors of the last term. Consider the signs. Since it is negative, one factor must be positive and one negative. | 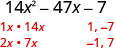 |
| Factors of \(14x^2\) | Pair with | Factors of −7 |
|---|---|---|
| \(x, 14 x\) | 11, −7 −7, 11 (reverse order) |
|
| \(x, 14 x\) | −1, 77 77, −1 (reverse order) |
|
| \(2x,7x\) | 11, −7 −7, 11 (reverse order) |
|
| \(2x,7x\) | −1, 77 77, −1 (reverse order) |
These pairings lead to the following eight combinations.
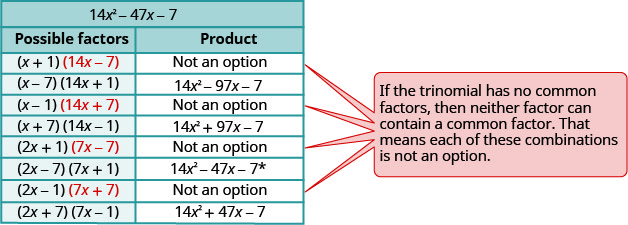
\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 x-7)(7 x+1)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 }\checkmark \end{array}\end{array}\)
Factor completely: \(8 a^{2}-3 a-5\)
- Answer
-
\((a-1)(8 a+5)\)
Factor completely: \(6 b^{2}-b-15\)
- Answer
-
\((2 b+3)(3 b-5)\)
Factor completely: \(18 n^{2}-37 n+15\)
Solution
| The trinomial is already in descending order. | \(18 n^{2}-37 n+15\) |
| Find the factors of the first term. | 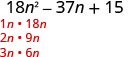 |
| Find the factors of the last term. Consider the signs. Since 15 is positive and the coefficient of the middle term is negative, we use the negative factors. | 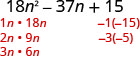 |
Consider all the combinations of factors.

\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 n-3)(9 n-5)\\\\\text {Check by multiplying. } \\\\ \begin{array}{l}{(2 n-3)(9 n-5)} \\ {18 n^{2}-10 n-27 n+15} \\ {18 n^{2}-37 n+15 } \checkmark\end{array} \end{array}\)
Factor completely: \(18 x^{2}-3 x-10\)
- Answer
-
\((3 x+2)(6 x-5)\)
Factor completely: \(30 y^{2}-53 y-21\)
- Answer
-
\((3 y+1)(10 y-21)\)
Don’t forget to look for a GCF first.
Factor completely: \(10 y^{4}+55 y^{3}+60 y^{2}\)
Solution
| \(10 y^{4}+55 y^{3}+60 y^{2}\) | |
| Notice the greatest common factor, and factor it first. | 5\(y^{2}\left(2 y^{2}+11 y+12\right)\) |
| Factor the trinomial. | 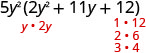 |
Consider all the combinations.
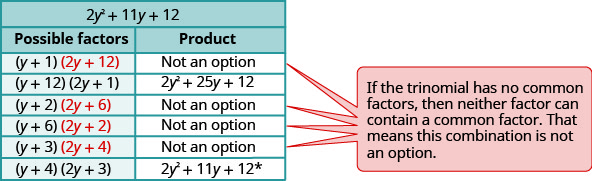
\(\begin{array}{ll}\text{The correct factors are those whose product} &5 y^{2}(y+4)(2 y+3) \\ \text{is the original trinomial. Remember to include} & \\\text {the factor } 5 y^{2}\\\text {Check by multiplying. } \\\\ \begin{array}{l}{5 y^{2}(y+4)(2 y+3)} \\ {5 y^{2}\left(2 y^{2}+8 y+3 y+12\right)} \\ {10 y^{4}+55 y^{3}+60 y^{2}}\checkmark\end{array} \end{array}\)
Factor completely: \(15 n^{3}-85 n^{2}+100 n\)
- Answer
-
5\(n(n-4)(3 n-5)\)
Factor completely: \(56 q^{3}+320 q^{2}-96 q\)
- Answer
-
8\(q(q+6)(7 q-2)\)
Factor Trinomials using the “ac” Method
Another way to factor trinomials of the form \(ax^2+bx+c\) is the “ac” method. (The “ac” method is sometimes called the grouping method.) The “ac” method is actually an extension of the methods you used in the last section to factor trinomials with leading coefficient one. This method is very structured (that is step-by-step), and it always works!
Factor: \(6 x^{2}+7 x+2\)
Solution


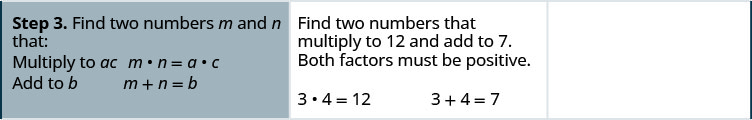



Factor: \(6 x^{2}+13 x+2\)
- Answer
-
\((x+2)(6 x+1)\)
Factor: \(4 y^{2}+8 y+3\)
- Answer
-
\((2 y+1)(2 y+3)\)
- Factor any GCF.
- Find the product ac.
- Find two numbers m and n that:
\(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\) - Split the middle term using m and n:
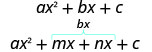
- Factor by grouping.
- Check by multiplying the factors.
When the third term of the trinomial is negative, the factors of the third term will have opposite signs.
Factor: \(8 u^{2}-17 u-21\)
Solution
| Is there a greatest common factor? No. | 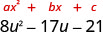 |
|
| Find \(a\cdot c\) | \(a\cdot c\) | |
| 8(−21) | ||
| −168 |
Find two numbers that multiply to −168 and add to −17. The larger factor must be negative.
| Factors of −168 | Sum of factors |
|---|---|
| 1,−168 | 1+(−168)=−167 |
| 2,−84 | 2+(−84)=−82 |
| 3,−56 | 3+(−56)=−53 |
| 4,−42 | 4+(−42)=−38 |
| 6,−28 | 6+(−28)=−22 |
| 7,−24 | 7+(−24)=−17* |
| 8,−21 | 8+(−21)=−13 |
\(\begin{array}{lc}\text { Split the middle term using } 7 u \text { and }-24 u &8 u^{2}-17 u-21 \\ & \qquad\space \swarrow\searrow \\ & \underbrace{8 u^{2}+7 u} \underbrace{-24 u-21} \\ \text { Factor by grouping. } & u(8 u+7)-3(8 u+7) \\ & (8 u+7)(u-3) \\ \text { Check by multiplying. } & \begin{array}{l}{(8 u+7)(u-3)} \\ {8 u^{2}-24 u+7 u-21} \\ {8 u^{2}-17 u-21} \checkmark \end{array} \end{array}\)
Factor: \(20 h^{2}+13 h-15\)
- Answer
-
\((4 h-5)(5 h+3)\)
Factor: \(6 g^{2}+19 g-20\)
- Answer
-
\((q+4)(6 q-5)\)
Factor: \(2 x^{2}+6 x+5\)
Solution
| Is there a greatest common factor? No. | 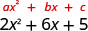 |
| Find a⋅c | a⋅c |
| 2(5) | |
| 10 |
Find two numbers that multiply to 10 and add to 6.
| Factors of 10 | Sum of factors |
|---|---|
| 1,10 | 1+10=11 |
| 2, 5 | 2+5=7 |
There are no factors that multiply to 10 and add to 6. The polynomial is prime.
Factor: \(10 t^{2}+19 t-15\)
- Answer
-
\((2 t+5)(5 t-3)\)
Factor: \(3 u^{2}+8 u+5\)
- Answer
-
\((u+1)(3 u+5)\)
Don’t forget to look for a common factor!
Factor: \(10 y^{2}-55 y+70\)
Solution
| Is there a greatest common factor? Yes. The GCF is 5. | 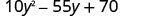 |
| Factor it. Be careful to keep the factor of 5 all the way through the solution! | 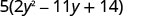 |
| The trinomial inside the parentheses has a leading coefficient that is not 1. | 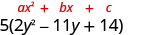 |
| Factor the trinomial. | 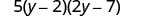 |
| Check by multiplying all three factors. | |
| 5\(\left(2 y^{2}-2 y-4 y+14\right)\) | |
| 5\(\left(2 y^{2}-11 y+14\right)\) | |
| \(10 y^{2}-55 y+70\) ✓ |
Factor: \(16 x^{2}-32 x+12\)
- Answer
-
4\((2 x-3)(2 x-1)\)
Factor: \(18 w^{2}-39 w+18\)
- Answer
-
3\((3 w-2)(2 w-3)\)
We can now update the Preliminary Factoring Strategy, as shown in Figure \(\PageIndex{1}\) and detailed in Choose a strategy to factor polynomials completely (updated), to include trinomials of the form \(a x^{2}+b x+c\). Remember, some polynomials are prime and so they cannot be factored.

- Is there a greatest common factor?
- Factor it.
- Is the polynomial a binomial, trinomial, or are there more than three terms?
- If it is a binomial, right now we have no method to factor it.
- If it is a trinomial of the form \(x^{2}+b x+c\)
Undo FOIL \\((x\qquad)(x\qquad)\). - If it is a trinomial of the form \(a x^{2}+b x+c\)
Use Trial and Error or the “ac” method. - If it has more than three terms
Use the grouping method.
- Check by multiplying the factors.
Access these online resources for additional instruction and practice with factoring trinomials of the form \(a x^{2}+b x+c\)
Key Concepts
- Factor Trinomials of the Form \(a x^{2}+b x+c\) using Trial and Error: See Example.
- Write the trinomial in descending order of degrees.
- Find all the factor pairs of the first term.
- Find all the factor pairs of the third term.
- Test all the possible combinations of the factors until the correct product is found.
- Check by multiplying.
- Factor Trinomials of the Form \(a x^{2}+b x+c\) Using the “ac” Method: See Example.
- Factor any GCF.
- Find the product ac.
- Find two numbers m and n that: \(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\)
- Split the middle term using m and n:
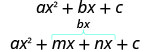
- Factor by grouping.
- Check by multiplying the factors.
- Choose a strategy to factor polynomials completely (updated):
- Is there a greatest common factor? Factor it.
- Is the polynomial a binomial, trinomial, or are there more than three terms?
If it is a binomial, right now we have no method to factor it.
If it is a trinomial of the form \(x^2+bx+c\)
Undo FOIL \((x\qquad)(x\qquad)\).
If it is a trinomial of the form \(ax^2+bx+c\)
Use Trial and Error or the “ac” method.
If it has more than three terms
Use the grouping method. - Check by multiplying the factors.
Glossary
- prime polynomials
- Polynomials that cannot be factored are prime polynomials.


