7.2E: Exercises

Practice Makes Perfect

Factor Trinomials of the Form $x^2+bx+c$

In the following exercises, factor each trinomial of the form $x^2+bx+c$

Exercise 1

$x^2+4x+3$

Answer

$(x+1)(x+3)$

Exercise 2

$y^2+8y+7$

Exercise 3

$m^2+12m+11$

Answer

$(m+1)(m+11)$

Exercise 4

$b^2+14b+13$

Exercise 5

$a^2+9a+20$

Answer

$(a+4)(a+5)$

Exercise 6

$m^2+7m+12$ ​​​​​

Exercise 7

$p^2+11p+30$

Answer

$(p+5)(p+6)$

Exercise 8

$w^2+10w+21$

Exercise 9

$n^2+19n+48$

Answer

$(n+3)(n+16)$

Exercise 10

$b^2+14b+48$

Exercise 11

$a^2+25a+100$

Answer

$(a+5)(a+20)$

Exercise 12

$u^2+101u+100$

Exercise 13

$x^2−8x+12$

Answer

$(x−2)(x−6)$

Exercise 14

$q^2−13q+36$

Exercise 15

$y^2−18y+45$

Answer

$(y−3)(y−15)$

Exercise 16

$m^2−13m+30$

Exercise 17

$x^2−8x+7$

Answer

$(x−1)(x−7)$

Exercise 18

$y^2−5y+6$

Exercise 19

$p^2+5p−6$

Answer

$(p−1)(p+6)$

Exercise 20

$n^2+6n−7$

Exercise 21

$y^2−6y−7$

Answer

$(y+1)(y−7)$

Exercise 22

$v^2−2v−3$

Exercise 23

$x^2−x−12$

Answer

$(x−4)(x+3)$

Exercise 24

$r^2−2r−8$

Exercise 25

$a^2−3a−28$

Answer

$(a−7)(a+4)$

Exercise 26

$b^2−13b−30$

Exercise 27

$w^2−5w−36$

Answer

$(w−9)(w+4)$

Exercise 28

$t^2−3t−54$

Exercise 29

$x^2+x+5$

Answer

prime

Exercise 30

$x^2−3x−9$

Exercise 31

$8−6x+x^2$

Answer

$(x−4)(x−2)$

Exercise 32

$7x+x^2+6$

Exercise 33

$x^2−12−11x$

Answer

$(x−12)(x+1)$

Exercise 34

$−11−10x+x^2$

​​​​​​Factor Trinomials of the Form $x^2+bxy+cy^2$

In the following exercises, factor each trinomial of the form $x^2+bxy+cy^2$

Exercise 33.2

$p^2+3pq+2q^2$

Answer

$(p+q)(p+2q)$

Exercise 34.2

$m^2+6mn+5n^2$

Exercise 35

$r^2+15rs+36s^2$

Answer

$(r+3s)(r+12s)$

Exercise 36

$u^2+10uv+24v^2$

Exercise 37

$m^2−12mn+20n^2$

Answer

$(m−2n)(m−10n)$

Exercise 38

$p^2−16pq+63q^2$

Exercise 39

$x^2−2xy−80y^2$

Answer

$(x+8y)(x−10y)$

Exercise 40

$p^2−8pq−65q^2$

Exercise 41

$m^2−64mn−65n^2$

Answer

$(m+n)(m−65n)$

Exercise 42

$p^2−2pq−35q^2$

Exercise 43

$a^2+5ab−24b^2$

Answer

$(a+8b)(a−3b)$

Exercise 44

$r^2+3rs−28s^2$

Exercise 45

$x^2−3xy−14y^2$

Answer

prime

Exercise 46

$u^2−8uv−24v^2$

Exercise 47

$m^2−5mn+30n^2$

Answer

prime

Exercise 48

$c^2−7cd+18d^2$

​​​​​​Mixed Practice

In the following exercises, factor each expression.

Exercise 49

$u^2−12u+36$

Answer

$(u−6)(u−6)$

Exercise 50

$w^2+4w−32$

Exercise 51

$x^2−14x−32$

Answer

$(x+2)(x−16)$

Exercise 52

$y^2+41y+40$

Exercise 53

$r^2−20rs+64s^2$

Answer

$(r−4s)(r−16s)$

Exercise 54

$x^2−16xy+64y^2$

Exercise 55

$k^2+34k+120$

Answer

$(k+4)(k+30)$

Exercise 56

$m^2+29m+120$

Exercise 57

$y^2+10y+15$

Answer

prime

Exercise 58

$z^2−3z+28$

Exercise 59

$m^2+mn−56n^2$

Answer

$(m+8n)(m−7n)$

Exercise 60

$q^2−29qr−96r^2$

Exercise 61

$u^2−17uv+30v^2$

Answer

$(u−15v)(u−2v)$

Exercise 62

$m^2−31mn+30n^2$

Exercise 63

$c^2−8cd+26d^2$

Answer

prime

Exercise 64

$r^2+11rs+36s^2$

Everyday Math

Exercise 65

Consecutive integers Deirdre is thinking of two consecutive integers whose product is 56. The trinomial $x^2+x−56$ describes how these numbers are related. Factor the trinomial.

Answer

$(x+8)(x−7)$

Exercise 66

Consecutive integers Deshawn is thinking of two consecutive integers whose product is 182. The trinomial $x^2+x−182$ describes how these numbers are related. Factor the trinomial describes how these numbers are related. Factor the trinomial.

​​​​​​Writing Exercises

Exercise 67

Many trinomials of the form $x^2+bx+c$ factor into the product of two binomials $(x+m)(x+n)$. Explain how you find the values of $m$ and $n$.

Answer

Answers may vary

Exercise 68

How do you determine whether to use plus or minus signs in the binomial factors of a trinomial of the form $x^2+bx+c$ where $b$ and $c$ may be positive or negative numbers?

Exercise 69

Will factored $x^2−x−20$ as $(x+5)(x−4)$. Bill factored it as $(x+4)(x−5)$. Phil factored it as $(x−5)(x−4)$. Who is correct? Explain why the other two are wrong.

Answer

Answers may vary

Exercise 70

Look at Example, where we factored $y^2+17y+60$. We made a table listing all pairs of factors of 60 and their sums. Do you find this kind of table helpful? Why or why not?

​​​​​Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

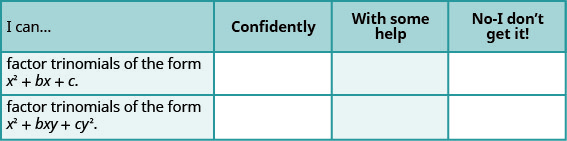
b. After reviewing this checklist, what will you do to become confident for all goals?