7.5: General Strategy for Factoring Polynomials

Learning Objectives

By the end of this section, you will be able to:

• Recognize and use the appropriate method to factor a polynomial completely

Note

Before you get started, take this readiness quiz.

1. Factor $y^{2}-2 y-24$.
   If you missed this problem, review Example 7.2.19.
2. Factor $3 t^{2}+17 t+10$.
   If you missed this problem, review Example 7.3.28.
3. Factor $36 p^{2}-60 p+25$.
   If you missed this problem, review Example 7.4.1.
4. Factor $5 x^{2}-80$.
   If you missed this problem, review Example 7.4.31.

Recognize and Use the Appropriate Method to Factor a Polynomial Completely

You have now become acquainted with all the methods of factoring that you will need in this course. (In your next algebra course, more methods will be added to your repertoire.) The figure below summarizes all the factoring methods we have covered. Figure $\PageIndex{1}$ outlines a strategy you should use when factoring polynomials.

Figure $\PageIndex{1}$

FACTOR POLYNOMIALS.

1. Is there a greatest common factor?
   • Factor it out.
2. Is the polynomial a binomial, trinomial, or are there more than three terms?
   • If it is a binomial:
     Is it a sum?
     • Of squares? Sums of squares do not factor.
     • Of cubes? Use the sum of cubes pattern.
     Is it a difference?
     • Of squares? Factor as the product of conjugates.
     • Of cubes? Use the difference of cubes pattern.
   • If it is a trinomial:
     Is it of the form $x^{2}+b x+c ?$? Undo FOIL.
     Is it of the form $a x^{2}+b x+c$?
     • If aa and cc are squares, check if it fits the trinomial square pattern.
     • Use the trial and error or “ac” method.
   • If it has more than three terms:
     Use the grouping method.
3. Check.
   • Is it factored completely?
   • Do the factors multiply back to the original polynomial?

Remember, a polynomial is completely factored if, other than monomials, its factors are prime!

Example $\PageIndex{1}$

Factor completely: $4 x^{5}+12 x^{4}$

Solution

$\begin{array}{lll} \text { Is there a GCF? } & \text { Yes, } 4 x^{4}& 4 x^{5}+12 x^{4} \\ \text { Factor out the GCF. } & &4 x^{4}(x+3) \\ \text { In the parentheses, is it a binomial, a } & & \\ \text { trinomial, or are there more than three terms? } & \text { Binomial. } & \\ \quad \text { Is it a sum? } & & \text { Yes. } \\ \quad \text { Of squares? Of cubes? } & & \text { No. }\\ \text { Check. } \\ \\ \quad \text { Is the expression factored completely? } & & \text{ Yes.} \\ \quad \text { Multiply. } \\ \begin{array}{l}{4 x^{4}(x+3)} \\ {4 x^{4} \cdot x+4 x^{4} \cdot 3} \\ {4 x^{5}+12 x^{4}}\checkmark \end{array}\end{array}$

Try It $\PageIndex{2}$

Factor completely: $3 a^{4}+18 a^{3}$

Answer

3$a^{3}(a+6)$

Try It $\PageIndex{3}$

Factor completely: $45 b^{6}+27 b^{5}$

Answer

9$b^{5}(5 b+3)$

Example $\PageIndex{4}$

Factor completely: $12 x^{2}-11 x+2$

Solution

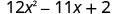Is there a GCF?	No.
Is it a binomial, trinomial, or are there more than three terms?	Trinomial.
Are a and c perfect squares?	No, a = 12, not a perfect square.
Use trial and error or the “ac” method. We will use trial and error here.

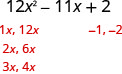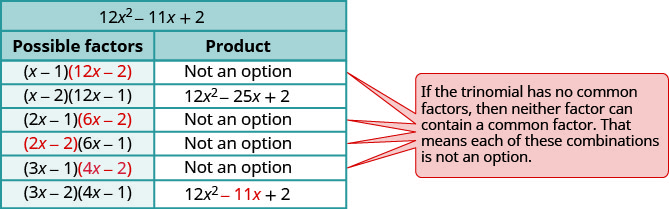Check. $\begin{array}{l}{(3 x-2)(4 x-1)} \\ {12 x^{2}-3 x-8 x+2} \\ {12 x^{2}-11 x+2 }\checkmark \end{array}$

Try It $\PageIndex{5}$

Factor completely: $10 a^{2}-17 a+6$

Answer

$(5 a-6)(2 a-1)$

Try It $\PageIndex{6}$

Factor completely: $8 x^{2}-18 x+9$

Answer

$(2 x-3)(4 x-3)$

Example $\PageIndex{7}$

Factor completely: $g^{3}+25 g$

Solution

$\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, g.} &g^{3}+25 g \\\text { Factor out the GCF. } & &g\left(g^{2}+25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \quad \text { Is it a sum? Of squares? } & \text { Yes. } & \text { Sums of squares are prime. } \\\text { Check. } \\ \\ \quad \text { Is the expression factored completely? } &\text { Yes. } \\ \quad \text { Multiply. } \\ \qquad \begin{array}{l}{g\left(g^{2}+25\right)} \\ {g^{3}+25 g }\checkmark \end{array} \end{array}$

Try It $\PageIndex{8}$

Factor completely: $x^{3}+36 x$

Answer

$x\left(x^{2}+36\right)$

Try It $\PageIndex{9}$

Factor completely: $27 y^{2}+48$

Answer

3$\left(9 y^{2}+16\right)$

Example $\PageIndex{10}$

Factor completely: $12 y^{2}-75$

Solution

$\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 3.} &12 y^{2}-75 \\\text { Factor out the GCF. } & &3\left(4 y^{2}-25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \text { Is it a sum?} & \text { No. } & \\ \text { Is it a difference? Of squares or cubes? } &\text { Yes, squares. } & 3\left((2 y)^{2}-(5)^{2}\right) \\ \text { Write as a product of conjugates. } & &3(2 y-5)(2 y+5)\\\text { Check. } \\ \\ \text { Is the expression factored completely? } & \text{ Yes.}& \\ \text { Neither binomial is a difference of } \\ \text { squares. } \\ \text{ Multiply.} \\ \quad \begin{array}{l}{3(2 y-5)(2 y+5)} \\ {3\left(4 y^{2}-25\right)} \\ {12 y^{2}-75}\checkmark \end{array} \end{array}$

Try It $\PageIndex{11}$

Factor completely: $16 x^{3}-36 x$

Answer

4$x(2 x-3)(2 x+3)$

Try It $\PageIndex{12}$

Factor completely: $27 y^{2}-48$

Answer

3$(3 y-4)(3 y+4)$

Example $\PageIndex{13}$

Factor completely: $4 a^{2}-12 a b+9 b^{2}$

Solution

Is there a GCF?	No.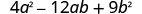
Is it a binomial, trinomial, or are there more terms?
Trinomial with $a\neq 1$. But the first term is a   perfect square.
Is the last term a perfect square?	Yes.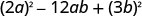
Does it fit the pattern, $a^{2}-2 a b+b^{2}$?	Yes.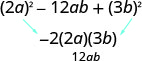
Write it as a square.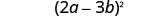
Check your answer.
Is the expression factored completely?
Yes.
The binomial is not a difference of squares.
Multiply.
$(2 a-3 b)^{2}$
$(2 a)^{2}-2 \cdot 2 a \cdot 3 b+(3 b)^{2}$
$4 a^{2}-12 a b+9 b^{2} \checkmark$

Try It $\PageIndex{14}$

Factor completely: $4 x^{2}+20 x y+25 y^{2}$

Answer

$(2 x+5 y)^{2}$

Try It $\PageIndex{15}$

Factor completely: $9 m^{2}+42 m n+49 n^{2}$

Answer

$(3 m+7 n)^{2}$

Example $\PageIndex{16}$

Factor completely: $6 y^{2}-18 y-60$

Solution

$\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 6.} &6 y^{2}-18 y-60 \\\text { Factor out the GCF. } & \text { Trinomial with leading coefficient } 1&6\left(y^{2}-3 y-10\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more terms? } & & \\ \text { "Undo' FOIL. } & 6(y\qquad )(y\qquad ) &6(y+2)(y-5) \\ \text { Check your answer. } \\ \text { Is the expression factored completely? } & & \text{ Yes.} \\ \text { Neither binomial is a difference of squares. } \\ \text { Multiply. } \\ \\\qquad \begin{array}{l}{6(y+2)(y-5)} \\ {6\left(y^{2}-5 y+2 y-10\right)} \\ {6\left(y^{2}-3 y-10\right)} \\ {6 y^{2}-18 y-60} \checkmark \end{array} \end{array}$

Try It $\PageIndex{17}$

Factor completely: $8 y^{2}+16 y-24$

Answer

8$(y-1)(y+3)$

Try It $\PageIndex{18}$

Factor completely: $5 u^{2}-15 u-270$

Answer

5$(u-9)(u+6)$

Example $\PageIndex{19}$

Factor completely: $24 x^{3}+81$

Solution

Is there a GCF?	Yes, 3.	$24 x^{3}+81$
Factor it out.		3$\left(8 x^{3}+27\right)$
In the parentheses, is it a binomial, trinomial, or are there more than three terms?	Binomial.
Is it a sum or difference?	Sum.
Of squares or cubes?	Sum of cubes.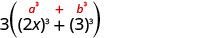
Write it using the sum of cubes pattern.
Is the expression factored completely?	Yes.	3$(2 x+3)\left(4 x^{2}-6 x+9\right)$
Check by multiplying.		We leave the check to you.

Try It $\PageIndex{20}$

Factor completely: $250 m^{3}+432$

Answer

2$(5 m+6)\left(25 m^{2}-30 m+36\right)$

Try It $\PageIndex{21}$

Factor completely: $81 q^{3}+192$

Answer

$3(3q+4)\left(9q^{2}-12 q+16\right)$

Example $\PageIndex{22}$

Factor completely: $2 x^{4}-32$

Solution

$\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &2 x^{4}-32 \\\text { Factor out the GCF. } & &2\left(x^{4}-16\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } & \text { Binomial. }& \\ \text { Is it a sum or difference? } &\text { Yes. }& \\\text { Of squares or cubes? } & \text { Difference of squares. } & 2\left(\left(x^{2}\right)^{2}-(4)^{2}\right) \\ \text { Write it as a product of conjugates. } & & 2\left(x^{2}-4\right)\left(x^{2}+4\right) \\ \text { The first binomial is again a difference of squares. } & & 2\left((x)^{2}-(2)^{2}\right)\left(x^{2}+4\right) \\ \text { Write it as a product of conjugates. } & & 2(x-2)(x+2)\left(x^{2}+4\right) \\ \text { Is the expression factored completely? } &\text { Yes. } & \\ \\ \text { None of these binomials is a difference of squares. } \\ \text { Check your answer. } \\ \text{ Multiply. }\\ \\ \qquad \qquad \begin{array}{l}{2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-10)} \\ {2 x^{4}-32} \checkmark \end{array} \end{array}$

Try It $\PageIndex{23}$

Factor completely: $4 a^{4}-64$

Answer

4$\left(a^{2}+4\right)(a-2)(a+2)$

Try It $\PageIndex{24}$

Factor completely: $7 y^{4}-7$

Answer

7$\left(y^{2}+1\right)(y-1)(y+1)$

Example $\PageIndex{25}$

Factor completely: $3 x^{2}+6 b x-3 a x-6 a b$

Solution

$\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 3.} &3 x^{2}+6 b x-3 a x-6 a b\\\text { Factor out the GCF. } & &3\left(x^{2}+2 b x-a x-2 a b\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { More than } 3 & \\ \text { or are there more terms? } &\text { terms. } & \\ \text { Use grouping. } & & \begin{array}{c}{3[x(x+2 b)-a(x+2 b)]} \\ {3(x+2 b)(x-a)}\end{array} \\ \text { Check your answer. } \\ \\ \text { Is the expression factored completely? Yes. } \\ \text { Multiply. } \\\qquad \qquad \begin{array}{l}{3(x+2 b)(x-a)} \\ {3\left(x^{2}-a x+2 b x-2 a b\right)} \\ {3 x^{2}-3 a x+6 b x-6 a b} \checkmark \end{array}\end{array}$

Try It $\PageIndex{26}$

Factor completely: $6 x^{2}-12 x c+6 b x-12 b c$

Answer

6$(x+b)(x-2 c)$

Try It $\PageIndex{27}$

Factor completely: $16 x^{2}+24 x y-4 x-6 y$

Answer

2$(4 x-1)(x+3 y)$

Example $\PageIndex{28}$

Factor completely: $10 x^{2}-34 x-24$

Solution

$\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &10 x^{2}-34 x-24\\\text { Factor out the GCF. } & &2\left(5 x^{2}-17 x-12\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { Trinomial with } & \\ \text { or are there more than three terms? } &\space a \neq 1 & \\ \text { Use trial and error or the "ac" method. } & & 2\left(5 x^{2}-17 x-12\right) \\ & & 2(5 x+3)(x-4) \\ \text { Check your answer. Is the expression factored } \\\text { completely? Yes. }\\ \\ \text { Multiply. } \\ \qquad \begin{array}{l}{2(5 x+3)(x-4)} \\ {2\left(5 x^{2}-20 x+3 x-12\right)} \\ {2\left(5 x^{2}-17 x-12\right)} \\ {10 x^{2}-34 x-24}\checkmark \end{array}\end{array}$

Try It $\PageIndex{29}$

Factor completely: $4 p^{2}-16 p+12$

Answer

4$(p-1)(p-3)$

Try It $\PageIndex{30}$

Factor completely: $6 q^{2}-9 q-6$

Answer

3$(q-2)(2 q+1)$

Key Concepts

• General Strategy for Factoring Polynomials See Figure $\PageIndex{1}$.
• How to Factor Polynomials
  1. Is there a greatest common factor? Factor it out.
  2. Is the polynomial a binomial, trinomial, or are there more than three terms?
     • If it is a binomial:
       Is it a sum?
       • Of squares? Sums of squares do not factor.
       • Of cubes? Use the sum of cubes pattern.
       Is it a difference?
       • Of squares? Factor as the product of conjugates.
       • Of cubes? Use the difference of cubes pattern.
     • If it is a trinomial:
       Is it of the form $x^{2}+b x+c$? Undo FOIL.
       Is it of the form $a x^{2}+b x+c$?
       • If ‘a’ and ‘c’ are squares, check if it fits the trinomial square pattern.
       • Use the trial and error or ‘ac’ method.
     • If it has more than three terms:
       Use the grouping method.
  3. Check. Is it factored completely? Do the factors multiply back to the original polynomial?