Chapter 2 Review Exercises
- Page ID
- 18072
Chapter Review Exercises
Use a General Strategy to Solve Linear Equations
Solve Equations Using the General Strategy for Solving Linear Equations
In the following exercises, determine whether each number is a solution to the equation.
1. \(10x−1=5x,\quad x= \frac{1}{5}\)
2. \(−12n+5=8n,\quad n=−\frac{5}{4}\)
- Answer
-
no
In the following exercises, solve each linear equation.
3. \(6(x+6)=24\)
4. \(−(s+4)=18\)
- Answer
-
\(s=−22\) so the solution set is: \( \{-22\} \).
5. \(23−3(y−7)=8\)
6. \(\frac{1}{3}(6m+21)=m−7\)
- Answer
-
\(m=−14\)
7. \(4(3.5y+0.25)=365\)
8. \(0.25(q−8)=0.1(q+7)\)
- Answer
-
\(q=18\)
9. \(8(r−2)=6(r+10)\)
10. \(5+7(2−5x)=2(9x+1)−(13x−57)\)
- Answer
-
\(x=−1\)
11. \((9n+5)−(3n−7)=20−(4n−2)\)
12. \(2[−16+5(8k−6)]=8(3−4k)−32\)
- Answer
-
\(k=\frac{3}{4}\)
Classify Equations
In the following exercises, classify each equation as a conditional equation, an identity, or a contradiction and then state the solution.
13. \(17y−3(4−2y)=11(y−1)+12y−1\)
14. \(9u+32=15(u−4)−3(2u+21)\)
- Answer
-
contradiction; no solution
15. \(−8(7m+4)=−6(8m+9)\)
Solve Equations with Fraction or Decimal Coefficients
In the following exercises, solve each equation.
16. \(\frac{2}{5}n−\frac{1}{10}=\frac{7}{10}\)
- Answer
-
\(n=2\)
17. \(\frac{3}{4}a−\frac{1}{3}=\frac{1}{2}a+\frac{5}{6}\)
18. \(\frac{1}{2}(k+3)=\frac{1}{3}(k+16)\)
- Answer
-
\(k=23\)
19. \(\frac{5y−1}{3}+4=\frac{-8y+4}{6}\)
20. \(0.8x−0.3=0.7x+0.2\)
- Answer
-
\(x=5\)
21. \(0.10d+0.05(d−4)=2.05\)
Use a Problem-Solving Strategy
Use a Problem Solving Strategy for Word Problems
In the following exercises, solve using the problem solving strategy for word problems.
22. Three-fourths of the people at a concert are children. If there are 87 children, what is the total number of people at the concert?
- Answer
-
There are 116 people.
23. There are nine saxophone players in the band. The number of saxophone players is one less than twice the number of tuba players. Find the number of tuba players.
Solve Number Word Problems
In the following exercises, solve each number word problem.
24. The sum of a number and three is forty-one. Find the number.
- Answer
-
38
25. One number is nine less than another. Their sum is negative twenty-seven. Find the numbers.
26. One number is two more than four times another. Their sum is negative thirteen. Find the numbers.
- Answer
-
\(−3,−10\)
27. The sum of two consecutive integers is \(−135\). Find the numbers.
28. Find three consecutive even integers whose sum is 234.
- Answer
-
76, 78, 80
29. Find three consecutive odd integers whose sum is 51.
30. Koji has $5,502 in his savings account. This is $30 less than six times the amount in his checking account. How much money does Koji have in his checking account?
- Answer
-
$922
Solve Percent Applications
In the following exercises, translate and solve.
31. What number is 67% of 250?
32. 12.5% of what number is 20?
- Answer
-
\(160\)
33. What percent of 125 is 150?
In the following exercises, solve.
34. The bill for Dino’s lunch was $19.45. He wanted to leave 20% of the total bill as a tip. How much should the tip be?
- Answer
-
\($3.89\)
35. Dolores bought a crib on sale for $350. The sale price was 40% of the original price. What was the original price of the crib?
36. Jaden earns $2,680 per month. He pays $938 a month for rent. What percent of his monthly pay goes to rent?
- Answer
-
\(35%\)
37. Angel received a raise in his annual salary from $55,400 to $56,785. Find the percent change.
38. Rowena’s monthly gasoline bill dropped from $83.75 last month to $56.95 this month. Find the percent change.
- Answer
-
\(32%\)
39. Emmett bought a pair of shoes on sale at 40% off from an original price of $138. Find ⓐ the amount of discount and ⓑthe sale price.
40. Lacey bought a pair of boots on sale for $95. The original price of the boots was $200. Find ⓐ the amount of discount and ⓑ the discount rate. (Round to the nearest tenth of a percent, if needed.)
- Answer
-
ⓐ \($105\) ⓑ \(52.5%\)
41. Nga and Lauren bought a chest at a flea market for $50. They re-finished it and then added a 350% mark-up. Find ⓐthe amount of the mark-up and ⓑ the list price.
Solve Simple Interest Applications
In the following exercises, solve.
42. Winston deposited $3,294 in a bank account with interest rate 2.6% How much interest was earned in five years?
- Answer
-
\($428.22\)
43. Moira borrowed $4,500 from her grandfather to pay for her first year of college. Three years later, she repaid the $4,500 plus $243 interest. What was the rate of interest?
44. Jaime’s refrigerator loan statement said he would pay $1,026 in interest for a four-year loan at 13.5%. How much did Jaime borrow to buy the refrigerator?
- Answer
-
\($1,900\)
Solve a formula for a Specific Variable
Solve a Formula for a Specific Variable
In the following exercises, solve the formula for the specified variable.
45. Solve the formula
\(V=LWH\) for L.
46. Solve the formula
\(A=\frac{1}{2}d_1d_2\) for \(d_2\).
- Answer
-
\(d_2=\frac{2A}{d_1}\)
47. Solve the formula
\(h=48t+\frac{1}{2}at^2\) for t.
48. Solve the formula
4x−3y=12 for y.
- Answer
-
\(y=\frac{4x}{3}−4\)
Use Formulas to Solve Geometry Applications
In the following exercises, solve using a geometry formula.
49. What is the height of a triangle with area 67.567.5 square meters and base 9 meters?
50. The measure of the smallest angle in a right triangle is 45°45° less than the measure of the next larger angle. Find the measures of all three angles.
- Answer
-
\(22.5°,\; 67.5°,\; 90°\)
51. The perimeter of a triangle is 97 feet. One side of the triangle is eleven feet more than the smallest side. The third side is six feet more than twice the smallest side. Find the lengths of all sides.
52. Find the length of the hypotenuse.
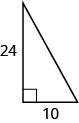
- Answer
-
\(26\)
53. Find the length of the missing side. Round to the nearest tenth, if necessary.
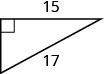
54. Sergio needs to attach a wire to hold the antenna to the roof of his house, as shown in the figure. The antenna is eight feet tall and Sergio has 10 feet of wire. How far from the base of the antenna can he attach the wire? Approximate to the nearest tenth, if necessary.
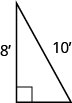
- Answer
-
6 feet
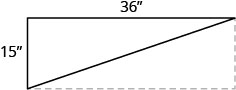
55. Seong is building shelving in his garage. The shelves are 36 inches wide and 15 inches tall. He wants to put a diagonal brace across the back to stabilize the shelves, as shown. How long should the brace be?
56. The length of a rectangle is 12 cm more than the width. The perimeter is 74 cm. Find the length and the width.
- Answer
-
\(24.5\) cm, \(12.5\) cm
57. The width of a rectangle is three more than twice the length. The perimeter is 96 inches. Find the length and the width.
58. The perimeter of a triangle is 35 feet. One side of the triangle is five feet longer than the second side. The third side is three feet longer than the second side. Find the length of each side.
- Answer
-
9 ft, 14 ft, 12 ft
Solve Mixture and Uniform Motion Applications
Solve Coin Word Problems
In the following exercises, solve.
59. Paulette has $140 in $5 and $10 bills. The number of $10 bills is one less than twice the number of $5 bills. How many of each does she have?
60. Lenny has $3.69 in pennies, dimes, and quarters. The number of pennies is three more than the number of dimes. The number of quarters is twice the number of dimes. How many of each coin does he have?
- Answer
-
nine pennies, six dimes, 12 quarters
Solve Ticket and Stamp Word Problems
In the following exercises, solve each ticket or stamp word problem.
61. Tickets for a basketball game cost $2 for students and $5 for adults. The number of students was three less than 10 times the number of adults. The total amount of money from ticket sales was $619. How many of each ticket were sold?
62. 125 tickets were sold for the jazz band concert for a total of $1,022. Student tickets cost $6 each and general admission tickets cost $10 each. How many of each kind of ticket were sold?
- Answer
-
57 students, 68 adults
63. Yumi spent $34.15 buying stamps. The number of $0.56 stamps she bought was 10 less than four times the number of $0.41 stamps. How many of each did she buy?
Solve Mixture Word Problems
In the following exercises, solve.
64. Marquese is making 10 pounds of trail mix from raisins and nuts. Raisins cost $3.45 per pound and nuts cost $7.95 per pound. How many pounds of raisins and how many pounds of nuts should Marquese use for the trail mix to cost him $6.96 per pound?
- Answer
-
\(2.2\) lbs of raisins, \(7.8\) lbs of nuts
65. Amber wants to put tiles on the backsplash of her kitchen counters. She will need 36 square feet of tile. She will use basic tiles that cost $8 per square foot and decorator tiles that cost $20 per square foot. How many square feet of each tile should she use so that the overall cost of the backsplash will be $10 per square foot?
66. Enrique borrowed $23,500 to buy a car. He pays his uncle 2% interest on the $4,500 he borrowed from him, and he pays the bank 11.5% interest on the rest. What average interest rate does he pay on the total $23,500? (Round your answer to the nearest tenth of a percent.)
- Answer
-
\(9.7%\)
Solve Uniform Motion Applications
In the following exercises, solve.
67. When Gabe drives from Sacramento to Redding it takes him 2.2 hours. It takes Elsa two hours to drive the same distance. Elsa’s speed is seven miles per hour faster than Gabe’s speed. Find Gabe’s speed and Elsa’s speed.
68. Louellen and Tracy met at a restaurant on the road between Chicago and Nashville. Louellen had left Chicago and drove 3.2 hours towards Nashville. Tracy had left Nashville and drove 4 hours towards Chicago, at a speed one mile per hour faster than Louellen’s speed. The distance between Chicago and Nashville is 472 miles. Find Louellen’s speed and Tracy’s speed.
- Answer
-
Louellen 65 mph, Tracy 66 mph
69. Two busses leave Amarillo at the same time. The Albuquerque bus heads west on the I-40 at a speed of 72 miles per hour, and the Oklahoma City bus heads east on the I-40 at a speed of 78 miles per hour. How many hours will it take them to be 375 miles apart?
70. Kyle rowed his boat upstream for 50 minutes. It took him 30 minutes to row back downstream. His speed going upstream is two miles per hour slower than his speed going downstream. Find Kyle’s upstream and downstream speeds.
- Answer
-
upstream 3 mph, downstream 5 mph
71. At 6:30, Devon left her house and rode her bike on the flat road until 7:30. Then she started riding uphill and rode until 8:00. She rode a total of 15 miles. Her speed on the flat road was three miles per hour faster than her speed going uphill. Find Devon’s speed on the flat road and riding uphill.
72. Anthony drove from New York City to Baltimore, which is a distance of 192 miles. He left at 3:45 and had heavy traffic until 5:30. Traffic was light for the rest of the drive, and he arrived at 7:30. His speed in light traffic was four miles per hour more than twice his speed in heavy traffic. Find Anthony’s driving speed in heavy traffic and light traffic.
- Answer
-
heavy traffic 32 mph, light traffic 66 mph
Solve Linear Inequalities
Graph Inequalities on the Number Line
In the following exercises, graph the inequality on the number line and write in interval notation.
73. \(x<−1\)
74. \(x\geq −2.5\)
- Answer
-
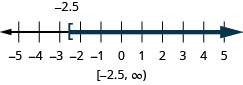
75. \(x\leq \frac{5}{4}\)
76. \(x>2\)
- Answer
-
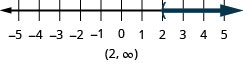
77. \(−2<x<0\)
78. \(-5\leq x<−3\)
- Answer
-
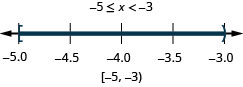
79. \(0\leq x\leq 3.5\)
Solve Linear Inequalities
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
80. \(n−12\leq 23\)
- Answer
-
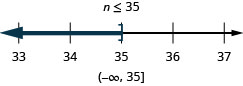
81. \(a+\frac{2}{3}\geq \frac{7}{12}\)
82. \(9x>54\)
- Answer
-
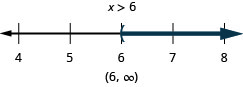
83. \(\frac{q}{−2}\geq −24\)
84. \(6p>15p−30\)
- Answer
-
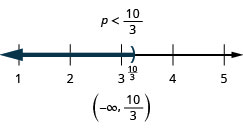
85. \(9h−7(h−1)\leq 4h−23\)
86. \(5n−15(4−n)<10(n−6)+10n\)
- Answer
-
87. \(\frac{3}{8}a−\frac{1}{12}a>\frac{5}{12}a+\frac{3}{4}\)
Translate Words to an Inequality and Solve
In the following exercises, translate and solve. Then write the solution in interval notation and graph on the number line.
88. Five more than \(z\) is at most 19.
- Answer
-
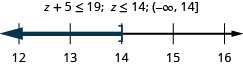
89. Three less than \(c\) is at least 360.
90. Nine times \(n\) exceeds 42.
- Answer
-
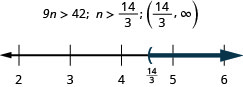
91. Negative two times \(a\) is no more than eight.
Solve Applications with Linear Inequalities
In the following exercises, solve.
92. Julianne has a weekly food budget of $231 for her family. If she plans to budget the same amount for each of the seven days of the week, what is the maximum amount she can spend on food each day?
- Answer
-
$33 per day
93. Rogelio paints watercolors. He got a $100 gift card to the art supply store and wants to use it to buy 12″ × 16″ canvases. Each canvas costs $10.99. What is the maximum number of canvases he can buy with his gift card?
94. Briana has been offered a sales job in another city. The offer was for $42,500 plus 8% of her total sales. In order to make it worth the move, Briana needs to have an annual salary of at least $66,500. What would her total sales need to be for her to move?
- Answer
-
at least $300,000
95. Renee’s car costs her $195 per month plus $0.09 per mile. How many miles can Renee drive so that her monthly car expenses are no more than $250?
96. Costa is an accountant. During tax season, he charges $125 to do a simple tax return. His expenses for buying software, renting an office, and advertising are $6,000. How many tax returns must he do if he wants to make a profit of at least $8,000?
- Answer
-
at least 112 jobs
97. Jenna is planning a five-day resort vacation with three of her friends. It will cost her $279 for airfare, $300 for food and entertainment, and $65 per day for her share of the hotel. She has $550 saved towards her vacation and can earn $25 per hour as an assistant in her uncle’s photography studio. How many hours must she work in order to have enough money for her vacation?
Solve Compound Inequalities
Solve Compound Inequalities with “and”
In each of the following exercises, solve each inequality, graph the solution, and write the solution in interval notation.
98. \(x\leq 5\) and \(x>−3\)
- Answer
-
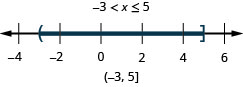
99. \(4x−2\leq 4\) and \(7x−1>−8\)
100. \(5(3x−2)\leq 5\) and \(4(x+2)<3\)
- Answer
-
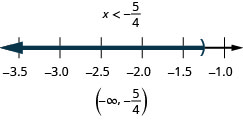
101. \(34(x−8)\leq 3\) and \(15(x−5)\leq 3\)
102. \(34x−5\geq −2\) and \(−3(x+1)\geq 6\)
- Answer
-
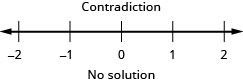
103. \(−5\leq 4x−1<7\)
Solve Compound Inequalities with “or”
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
104. \(5−2x\leq −1\) or \(6+3x\leq 4\)
- Answer
-
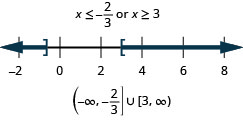
105. \(3(2x−3)<−5\) or \(4x−1>3\)
106. \(34x−2>4\) or \(4(2−x)>0\)
- Answer
-
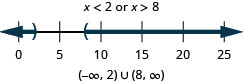
107. \(2(x+3)\geq 0\) or \(3(x+4)\leq 6\)
108. \(12x−3\leq 4\) or \(13(x−6)\geq −2\)
- Answer
-
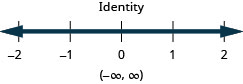
Solve Applications with Compound Inequalities
In the following exercises, solve.
109. Liam is playing a number game with his sister Audry. Liam is thinking of a number and wants Audry to guess it. Five more than three times her number is between 2 and 32. Write a compound inequality that shows the range of numbers that Liam might be thinking of.
110. Elouise is creating a rectangular garden in her back yard. The length of the garden is 12 feet. The perimeter of the garden must be at least 36 feet and no more than 48 feet. Use a compound inequality to find the range of values for the width of the garden.
- Answer
-
\(6\leq w\leq 12\)
Solve Absolute Value Inequalities
Solve Absolute Value Equations
In the following exercises, solve.
111. \(|x|=8\)
112. \(|y|=−14\)
- Answer
-
no solution
113. \(|z|=0\)
114. \(|3x−4|+5=7\)
- Answer
-
\(x=2,x=\frac{2}{3}\)
115. \(4|x−1|+2=10\)
116. \(−2|x−3|+8=−4\)
- Answer
-
\(x=9,x=−3\)
117. \(|12x+5|+4=1\)
118. \(|6x−5|=|2x+3|\)
- Answer
-
\(x=2,x=14\)
Solve Absolute Value Inequalities with “less than”
In the following exercises, solve each inequality. Graph the solution and write the solution in interval notation.
119. \(|x|\leq 8\)
120. \(|2x−5|\leq 3\)
- Answer
-
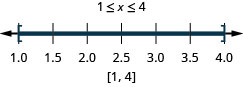
121. \(|6x−5|<7\)
122. \(|5x+1|\leq −2\)
- Answer
-
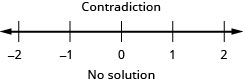
Solve Absolute Value Inequalities with “greater than”
In the following exercises, solve. Graph the solution and write the solution in interval notation.
123. \(|x|>6\)
124. \(|x|\geq 2\)
- Answer
-
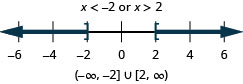
125. \(|x−5|>−2\)
126. \(|x−7|\geq 1\)
- Answer
-
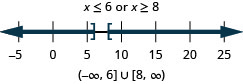
127. \(3|x|+4\geq 1\)
Solve Applications with Absolute Value
In the following exercises, solve.
128. A craft beer brewer needs 215,000 bottle per day. But this total can vary by as much as 5,000 bottles. What is the maximum and minimum expected usage at the bottling company?
- Answer
-
The minimum to maximum expected usage is 210,000 to 220,000 bottles
129. At Fancy Grocery, the ideal weight of a loaf of bread is 16 ounces. By law, the actual weight can vary from the ideal by 1.5 ounces. What range of weight will be acceptable to the inspector without causing the bakery being fined?
Practice Test
In the following exercises, solve each equation.
1. \(−5(2x+1)=45\)
- Answer
-
\(x=−5\)
2. \(\frac{1}{4}(12m+28)=6+2(3m+1)\)
3. \(8(3a+5)−7(4a−3)=20−3a\)
- Answer
-
\(a=41\)
4. \(0.1d+0.25(d+8)=4.1\)
5. \(14n−3(4n+5)=−9+2(n−8) \)
- Answer
-
contradiction; no solution
6. \(3(3u+2)+4[6−8(u−1)]=3(u−2)\)
7. \(\frac{3}{4}x−\frac{2}{3}=\frac{1}{2}x+\frac{5}{6}\)
- Answer
-
\(x=6\)
8. \(|3x−4|=8\)
9. \(|2x−1|=|4x+3|\)
- Answer
-
\(x=−2,x=−13\)
10. Solve the formula
\(x+2y=5\) for y.
In the following exercises, graph the inequality on the number line and write in interval notation.
11. \(x\geq −3.5\)
- Answer
-
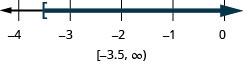
12. \(x<\frac{11}{4}\)
13. \(−2\leq x<5\)
- Answer
-
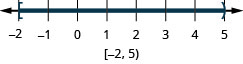
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
14. \(8k\geq 5k−120\)
15. \(3c−10(c−2)<5c+16\)
- Answer
-
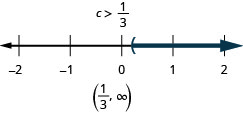
16. \(\frac{3}{4}x−5\geq −2\) and \(−3(x+1)\geq 6\)
17. \(3(2x−3)<−5\) or \(4x−1>3\)
- Answer
-
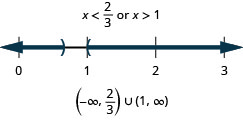
18. \(\frac{1}{2}x−3\leq 4\) or \(\frac{1}{3}(x−6)\geq −2\)
19. \(|4x−3|\geq 5\)
- Answer
-
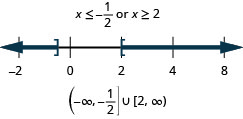
In the following exercises, translate to an equation or inequality and solve.
20. Four less than twice x is 16.
21. Find the length of the missing side.
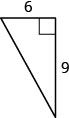
- Answer
-
\(10.8\)
22. One number is four more than twice another. Their sum is \(−47\). Find the numbers.
23. The sum of two consecutive odd integers is \(−112\). Find the numbers.
- Answer
-
\(−57,−55\)
24. Marcus bought a television on sale for $626.50 The original price of the television was $895. Find ⓐ the amount of discount and ⓑ the discount rate.
25. Bonita has $2.95 in dimes and quarters in her pocket. If she has five more dimes than quarters, how many of each coin does she have?
- Answer
-
12 dimes, seven quarters
26. Kim is making eight gallons of punch from fruit juice and soda. The fruit juice costs $6.04 per gallon and the soda costs $4.28 per gallon. How much fruit juice and how much soda should she use so that the punch costs $5.71 per gallon?
27. The measure of one angle of a triangle is twice the measure of the smallest angle. The measure of the third angle is three times the measure of the smallest angle. Find the measures of all three angles.
- Answer
-
\(30°,60°,90°\)
28. The length of a rectangle is five feet more than four times the width. The perimeter is 60 feet. Find the dimensions of the rectangle.
29. Two planes leave Dallas at the same time. One heads east at a speed of 428 miles per hour. The other plane heads west at a speed of 382 miles per hour. How many hours will it take them to be 2,025 miles apart?
- Answer
-
\(2.5\) hours
30. Leon drove from his house in Cincinnati to his sister’s house in Cleveland, a distance of 252 miles. It took him \(4\frac{1}{2}\) hours. For the first half hour, he had heavy traffic, and the rest of the time his speed was five miles per hour less than twice his speed in heavy traffic. What was his speed in heavy traffic?
31. Sara has a budget of $1,000 for costumes for the 18 members of her musical theater group. What is the maximum she can spend for each costume?
- Answer
-
At most $55.56 per costume.


