8.4: Applications

Last updated
Save as PDF

Page ID: 41320

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1.4 Applications
Trigonometry is often used for what is called "indirect measurement." This is a method of measuring inaccessible distances by using the relationships between lengths and angles within a triangle. Two simple examples of this process are measuring the height of a tall tree and measuring the distance across a body of water. In both cases, while it might be possible to measure the distance directly, it is often much easier to use indirect measurement.

In one example of indirect measurement, the angle of elevation of an object can be used to create a right triangle in which one angle and one side are known. The other sides of the triangle may then be solved for. In the problems in this text, the angle of elevation will typically be given in the problem. In order to actually measure the angle of elevation of an object, it is possible to use a simple protractor.

If you wanted to measure the height of a tall tree that sits on flat ground, you could use a specially modified protractor to do this. Modifying the protractor by tying a weight to the end of a string and tying the other end of the string through the hole in the protractor will help to measure the angle of elevation. Once the protractor is ready, hold it upside down and sight the top of the tree along the straight edge of the protractor. The weight hanging down will show the complement to the angle of elevation. In other words, if the angle of elevation is $20^{\circ},$ the string will mark out a measurement of $70^{\circ}$ on the protractor.

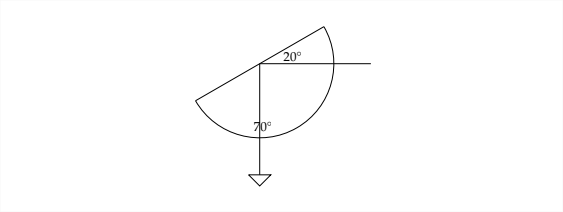
$clipboard_e13b0c9aa39c42f791e750fadf27ced45.png$

Closely related to the concept of the angle of elevation is the angle of depression. This is the angle that is formed by looking down on something from above.

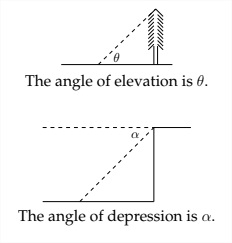
$clipboard_e06498bfd1d9482316539f4089e0412bc.png$

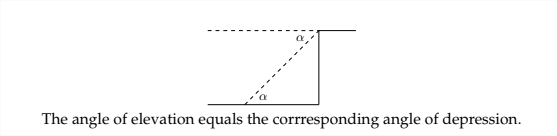
In a situation in which the angle of depression is measured, the angle of elevation and the angle of depression are alternate interior angles, which makes them equal.

$clipboard_ea27b958c116f82e8e5ce27111e5c8a87.png$

Example 1
Pacing off $100 \mathrm{ft}$ on flat ground from the base of a tree, a forester measures the angle of elevation to the top of the tree as $65^{\circ} .$ What is the height of the tree?
The situation described in the problem creates a diagram like the one below:
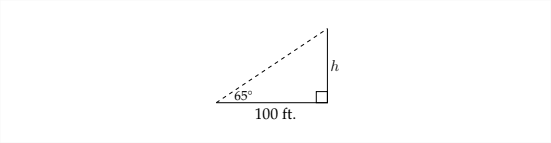
$clipboard_eef227133fd7b4c2d6401b9dc822fdce8.png$
since this is a right triangle, we can use an appropriate trigonometric ratio to find the height of the tree. In this case,
\[ \tan 65^{\circ}=\frac{h}{100}
\] $100 * \tan 65^{\circ}=h$
$214.45 \approx h$
So, the tree is about 214.45 feet tall.
Example 2
From the top of a building 125 feet tall, the angle of depression of an intersection
is $34^{\circ} .$ How far from the base of the building is the intersection?
As in the previous example, it is often helpful to draw a diagram.
$clipboard_e15cc6cb037d1820dc2cd7e865eb970c7.png$

Again, the angle of elevation will be equal to the corresponding angle of depression, so we can use the triangle as seen below to solve the problem:
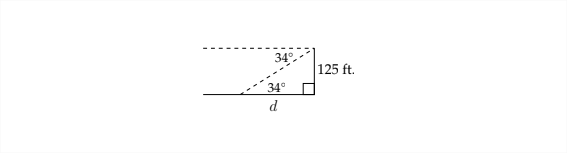
$clipboard_ee5e37044178743df9aadcfd19e7fa82f.png$
In this problem
\[ \tan 34^{\circ}=\frac{125}{d}
\] Multiply on both sides by $d$
\[ d * \tan 34^{\circ}=125
\] Then divide on both sides by $\tan 34^{\circ}$
\[ \begin{array}{c}
\frac{d \tan 34^{\circ}}{\tan 34^{\circ}}=\frac{125}{\tan 34^{\circ}} \\
d \approx 185.32
\end{array}
\]

Example 3
Sometimes a problem involves both an angle of elevation and an angle of depression.

From the roof of a house 20 feet off the ground, the angle of elevation of the top of an apartment building is $63^{\circ}$ and the angle of depression to the base of the building is $24^{\circ} .$ How far away from the house is the apartment building? How tall is the apartment building?

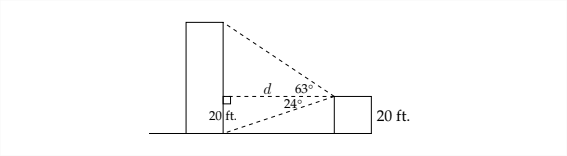
$clipboard_e6ee9f53eee59451645654fdaf6636fca.png$

If we work on the bottom triangle first, then we know that the height of the triangle is $20 \mathrm{ft}$ and the angle opposite this side is $24^{\circ} .$ So, we can say that:
\[ \begin{array}{c}
\tan 24^{\circ}=\frac{20}{d} \\
d=\frac{20}{\tan 24^{\circ}} \\
d \approx 45 \mathrm{ft}
\end{array}
\] Now that we know that the apartment building is 45 feet away, we can use the upper triangle to determine the height ofthe building.

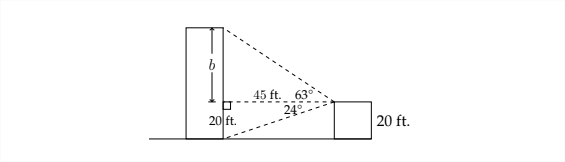
$clipboard_e3fb422c849ddcb22cdf677173370e8c5.png$

\[ \begin{array}{c}
\tan 63^{\circ}=\frac{b}{45} \\
45 * \tan 63^{\circ}=b \\
88.3 \mathrm{ft} . \approx b \\
20+88.3=108.3 \mathrm{ft}
\end{array}
\] since the variable $b$ only represents the part of the building that is in the second triangle, we need to add 20 feet to $b$ to find the actual height of the building.

Problems on bearing and direction
Some applications of trigonometry involve ship navigation. One common method used to describe direction in this type of problem is what is known as bearing. Bearing describes a direction by the angle deviation from north or south. For example, the direction we typically describe as northeast is exactly halfway between north and east. The bearing for northeast would be $N 45^{\circ} E$, and is read as "Forty-five degrees east of north."

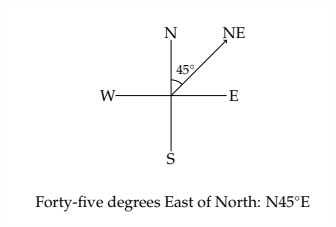
$clipboard_e64a69e0dcd5b759673704ac2da5e0ced.png$

Here are a few examples of what a bearing looks like in a N-S-E-W diagram.

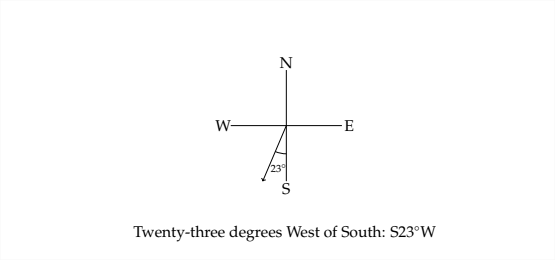
$clipboard_ee7caa1975ccdc5fb8f5a94df3023fe3b.png$

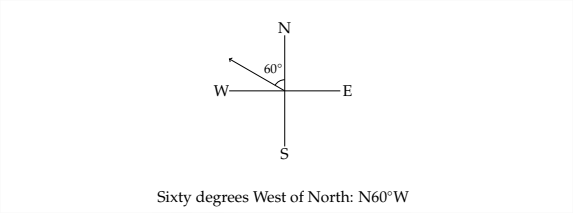
$clipboard_eba2b44a573a0337fd7d76ab16a969e6e.png$

Example 4
Santa Rosa, California is 7 miles due north of Rohnert Park. Bodega Bay is 19 miles due west of Rohnert Park (as the crow flies). What is the bearing of Santa Rosa from Bodega Bay?
First, it would be helpful to draw a diagram to represent the situation:

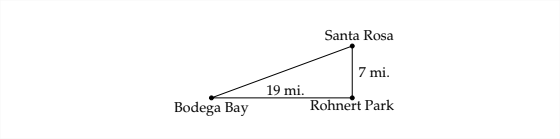
$clipboard_eeb44764ed9416885826cfb817488a521.png$

To answer the question we'll need another diagram:

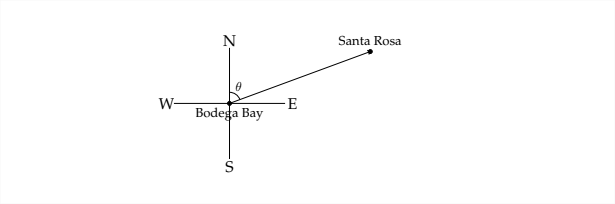
$clipboard_ec41d58665fc17d7bf1b0b32f1a0dece0.png$

If we knew the angle $\theta$, then we could conclude that the bearing of Santa Rosa from Bodega Bay is $\theta$ degrees East of North. From the previous diagram:
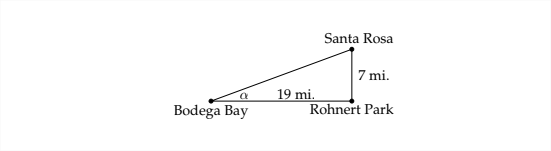
$clipboard_ebebd55c5df0dfbbc08824d491978cd6b.png$
we can see that we can't find $\theta$ directly, but we can find the complement of $\theta$
\[ \tan \alpha=\frac{7}{19}
\] $\alpha \approx 20.2^{\circ}$
\[ \text { Therefore, } \theta \approx 90^{\circ}-20.2^{\circ} \approx 69.8^{\circ}
\] That means that the bearing of Santa Rosa from Bodega Bay is $N 69.8^{\circ} E$, or $69.8^{\circ}$ East
of North.

Exercises 1.4
Round answers to the nearest $10^{t h}$
1. From the top of a lighthouse 180 feet above sea level, the angle of depression to a ship in the ocean is $28^{\circ} .$ How far is the ship from the base of the lighthouse?
2. A helicopter that is 700 feet in the air measures the angle of depression to a landing pad as $24^{\circ} .$ How far is the landing pad from the point directly beneath the helicopter's current position?
3. An 88 foot tree casts a shadow that is 135 feet long. What is the angle of elevation of the sun?
4. $\quad$ A 275 foot guy wire is attached to the top of a communication tower. If the wire makes an angle of $53^{\circ}$ with the ground, how tall is the tower?
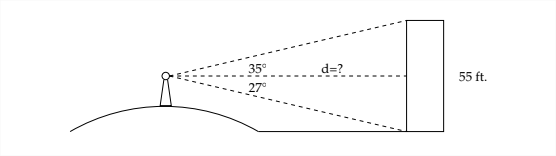
5. A woman standing on a hill sees a building that she knows is 55 feet tall. The angle of depression to the bottom of the building is $27^{\circ}$ and the angle of elevation to the top of the building is $35^{\circ} .$ Find the straight line distance from the woman to the building.

$clipboard_eab9902075f71f01de6d92facf3b98859.png$

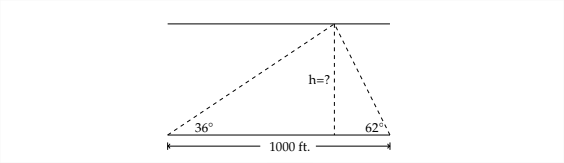
6. To measure the height of the cloud cover at an airport, a spotlight is shined upward at an angle of $62^{\circ} .$ An observer 1000 feet away measures the angle of elevation to the spotlight to be $36^{\circ} .$ Find the height of the cloud cover.
$clipboard_eff5f5f00f8e7d4c2803f8e250457c947.png$
7. At ground level, a water tower is 430 feet from the base of a building. From one of the upper floors of the building, the angle of elevation to the top of the water tower is $15^{\circ}$ and the angle of depression to the bottom of the water tower is $28^{\circ} .$ How tall is the water tower? How high off the ground is the observer?
8. A small airplane is flying at the altitude of 7000 feet following a straight road directly beneath it. A car in front of the airplane is sighted with an angle of depression of $72^{\circ}$ and a car behind the plane is sighted with an angle of depression of $48^{\circ} .$ How far apart are the cars?
9. From a point on the floor, the angle of elevation to the top of a doorway is 43". The angle of elevation to the ceiling directly above the doorway is $56^{\circ} .$ If the ceiling is 10 feet above the floor, how high is the doorway? How far in front of the doorway were the angles of elevation measured?
10. A man standing on the roof of a building 70 feet high looks at the building next door. The angle of depression to the roof of the building next door is $36^{\circ}$ The angle of depression to the bottom of the building next door is $65^{\circ} .$ How tall is the building next door?
11. A boat leaves the harbor and travels 30 miles in the direction of $N 38^{\circ} W$ The boat turns $90^{\circ}$ and then travels in the direction $S 52^{\circ} W$ for 12 miles. At that time, how far is the boat from the harbor and what is the bearing of the boat from the harbor entrance?

12. A man walking in the desert travels 1.6 miles in the direction $S 57^{\circ} E .$ He then turns $90^{\circ}$ and continues walking for 3.2 miles in the direction $N 33^{\circ} E .$ At that time, how far is he from his starting point and what is his bearing from the starting point?
13. Madras, Oregon is 26 miles due north of Redmond. Prineville is due east of Redmond and $S 34^{\circ} 42^{\prime} E$ from Madras. How far is Prineville from Redmond?
14. Raymond, Washington is 22 miles due south of Aberdeen. Montesano is due east of Aberdeen and $N 26^{\circ} 34^{\prime} E$ from Raymond. How far is Montesano from Raymond?
15. A boat travels on a course bearing of $S 41^{\circ} 40^{\prime} W$ for 84 miles. How far south and how far west is the boat from its starting point?
16. A boat travels on a course bearing of $N 17^{\circ} 10^{\prime} E$ for 10 miles. How far north and how far east is the boat from its starting point?