8.5: More Applications

Last updated
Save as PDF

Page ID: 41321

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1.5 More Applications
Sometimes solving problems involving right triangles requires the use of a system of equations. A common method for determining the height of an object whose base is inaccessible is that of measuring the angle of elevation from two different places in front of the object. If you measure the angle of elevation to the top of of a radio antenna as 74 , then walk back 50 feet and measure the angle of elevation to the top of the antenna as 61 ', then we would have something like the diagram below:
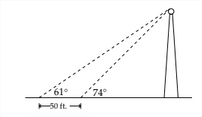
$clipboard_e9d77e4a8da0b7038b07812ec941d4551.png$
One of the first things we can do is introduce some labels for the unknown distances:
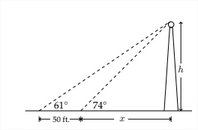
$clipboard_e1aadd8f7694a34b66a329e592c7f0a78.png$
Then, we can say that:
$\tan 74^{\circ}=\frac{h}{x}$
$\tan 61^{\circ}=\frac{h}{x+50}$

To solve this system of equations, we'll set the first one equal to $h:$
\[ \begin{array}{c}
\tan 74^{\circ}=\frac{h}{x} \\
x * \tan 74^{\circ}=h
\end{array}
\] Then, substitute this into the second equation:
\[ \tan 61^{\circ}=\frac{h}{x+30}
\] \[ \tan 61^{\circ}=\frac{x \tan 74^{\circ}}{x+50}
\] Multiply on both sides by $x+50:$
$(x+50) \tan 61^{\circ}=\frac{x \tan 74^{\circ}}{x+30}(x+50)$
$(x+50) \tan 61^{\circ}=x \tan 74^{\circ}$
There are two options to solve this equation - we can hold on to the tangents
as they are and solve for $x$ in terms $\tan 74^{\circ}$ and $\tan 61^{\circ},$ or we can approximate $\tan 74^{\circ}$ and $\tan 61^{\circ}$ and generate an approximate value for $x$ and $h .$ First we'll approximate:
$(x+50) \tan 61^{\circ}=x \tan 74^{\circ}$
\[ (x+50) * 1.804 \approx 3.4874 x
\] $1.804 x+90.2024 \approx 3.4874 x$
$90.2024 \approx 1.6834 x$

\[ 53.58 \approx x
\] $x * \tan 74^{\circ}=h$
\[ \begin{array}{c}
53.58 * \tan 74^{\circ} \approx h \\
186.87 \text { feet } \approx h
\end{array}
\] The other method is a little tricky algebraically:
\[ (x+50) \tan 61^{\circ}=x \tan 74^{\circ}
\] \[ \begin{array}{l}
x \tan 61^{\circ}+50 \tan 61^{\circ}=x \tan 74^{\circ} \\
50 \tan 61^{\circ}=x \tan 74^{\circ}-x \tan 61^{\circ} \\
50 \tan 61^{\circ}=x\left(\tan 74^{\circ}-\tan 61^{\circ}\right) \\
\frac{50 \tan 61^{\circ}}{\left(\tan 74^{\circ}-\tan 61^{\circ}\right)}=x
\end{array}
\] At this point, you can approximate the value of $x$ and solve for $h$, or express the value of $h$ exactly as
\[ \tan 74^{\circ} * \frac{50 \tan 61^{\circ}}{\left(\tan 74^{\circ}-\tan 61^{\circ}\right)}=h
\]

Exercises 1.5
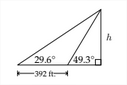
1. Find the indicated height $h$
$clipboard_e1e3996f82aeb0b97991146463fcea77d.png$
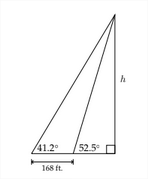
2. Find the indicated height $h$
$clipboard_e6af12b844fbee52557d8fb89fe02959a.png$
3. A small airplane flying at an altitude of 5300 feet sights two cars in front of the plane traveling on a road directly beneath it. The angle of depression to the nearest car is $62^{\circ}$ and the angle of depression to the more distant car is $41^{\circ}$. How far apart are the cars?
4. A hot air balloon is flying above a straight road. In order to estimate their altitude, the people in the balloon measure the angles of depression to two consecutive mile markers on the same side of the balloon. The angle to the doser marker is $17^{\circ}$ and the angle to the farther one is $13^{\circ} .$ At what altitude is the balloon flying?
5. To estimate the height of a mountain, the angle of elevation from a spot
on level ground to the top of the mountain is measured to be $32^{\circ} .$ From a point

1000 feet closer to the mountain, the angle of elevation is measured to be $35^{\circ}$ How high is the mountain above the ground from which the measurements were taken?
6. The angle of elevation from a point on the ground to the top of a pyramid is $35^{\circ} 30^{\prime} .$ The angle of elevation from a point 135 feet farther back to the top of the pyramid is $21^{\circ} 10$. What is the height of the pyramid?
7. An observer in a lighthouse 70 feet above sea level sights the angle of depression of an approaching ship to be $15^{\circ} 50^{\prime} .$ A few minutes later the angle of depression is sighted at $35^{\circ} 40^{\prime} .$ Find the distance traveled by the ship during that time.
8. To estimate the height of a tree, one forester stands due west of the tree and another forester stands due north of the tree. The two foresters are the same distance from the base of the tree and they are 45 feet from each other. If the angle of elevation for each forester is $40^{\circ},$ how tall is the tree?
9. A ship is anchored off of a long straight shoreline that runs east to west. From two observation points located 10 miles apart on the shoreline, the bearings of the ship from each observation point are $S 35^{\circ} E$ and $S 17^{\circ} W .$ How far from shore is the ship?
10. From fire lookout Station Alpha the bearing of a forest fire is $N 52^{\circ} E .$ From lookout Station Beta, sited 6 miles due east of Station Alpha, the bearing is $N 38^{\circ} \mathrm{W}$ How far is the fire from Station Alpha?
11. From a point 200 feet from the base of a church, the angle of elevation to the top of the steeple is $28^{\circ},$ while the angle of elevation to the bottom of the steeple is $20^{\circ} .$ How high off the ground is the top of the steeple?
12. A television tower 75 feet tall is installed on the top of a building. From a point on the ground in front of the building, the angle of elevation to the top of the tower is $62^{\circ}$ and the the angle of elevation to the bottom of the tower is $44^{\circ} .$ How tall is the building?