10.1: Reciprocal and Pythagorean Identities

The two most basic types of trigonometric identities are the reciprocal identities and the Pythagorean identities. The reciprocal identities are simply definitions of the reciprocals of the three standard trigonometric ratios:
\[ \sec \theta=\frac{1}{\cos \theta} \quad \csc \theta=\frac{1}{\sin \theta} \quad \cot \theta=\frac{1}{\tan \theta}
\]

Also, recall the definitions of the three standard trigonometric ratios (sine, cosine and tangent):
\[ \begin{array}{l}
\sin \theta=\frac{o p p}{h y p} \\
\cos \theta=\frac{a d j}{h y p} \\
\tan \theta=\frac{o p p}{a d y}
\end{array}
\]

If we look more closely at the relationships between the sine, cosine and tangent, we'll notice that \(\frac{\sin \theta}{\cos \theta}=\tan \theta\)
\[ \frac{\sin \theta}{\cos \theta}=\frac{\left(\frac{o p p}{h y p}\right)}{\left(\frac{a d j}{h y p}\right)}=\frac{o p p}{h y p} * \frac{h y p}{a d j}=\frac{o p p}{a d j}=\tan \theta
\]

Pythagorean Identities
The Pythagorean Identities are, of course, based on the Pythagorean Theorem. If we recall a diagram that was introduced in Chapter \(2,\) we can build these identities from the relationships in the diagram:

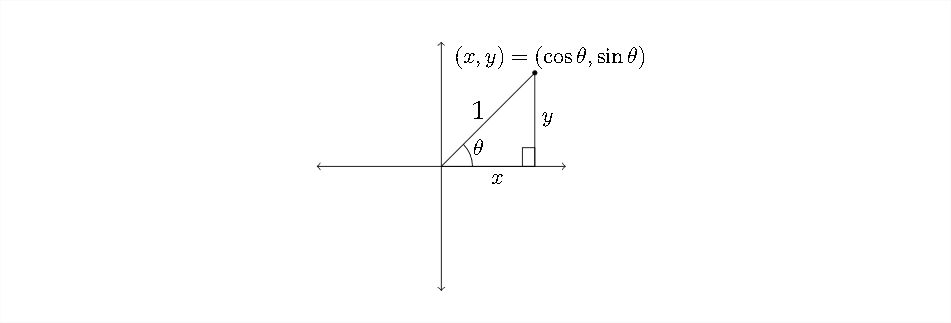
Using the Pythagorean Theorem in this diagram, we see that \(x^{2}+y^{2}=1^{2},\) so \(x^{2}+y^{2}=1 .\) But, also remember that, in the unit circle, \(x=\cos \theta\) and \(y=\sin \theta\)

Substituting this equality gives us the first Pythagorean Identity:
\[ x^{2}+y^{2}=1
\] or
\[ \cos ^{2} \theta+\sin ^{2} \theta=1
\] This identity is usually stated in the form:
\[ \sin ^{2} \theta+\cos ^{2} \theta=1
\]

If we take this identity and divide through on both sides by \(\cos ^{2} \theta,\) this will result in the first of two additional Pythagorean Identities:
\[ \frac{\sin ^{2} \theta}{\cos ^{2} \theta}+\frac{\cos ^{2} \theta}{\cos ^{2} \theta}=\frac{1}{\cos ^{2} \theta}
\] or
\[ \tan ^{2} \theta+1=\sec ^{2} \theta
\]

Dividing through by \(\sin ^{2} \theta\) gives us the second:
\[ \frac{\sin ^{2} \theta}{\sin ^{2} \theta}+\frac{\cos ^{2} \theta}{\sin ^{2} \theta}=\frac{1}{\sin ^{2} \theta}
\] or
\[ 1+\cot ^{2} \theta=\csc ^{2} \theta
\] So, the three Pythagorean Identities we will be using are:
\[ \begin{array}{l}
\sin ^{2} \theta+\cos ^{2} \theta=1 \\
\tan ^{2} \theta+1=\sec ^{2} \theta \\
1+\cot ^{2} \theta=\csc ^{2} \theta
\end{array}
\]

These Pythagorean Identities are often stated in other terms, such as:
\[ \begin{array}{l}
\sin ^{2} \theta=1-\cos ^{2} \theta \\
\cos ^{2} \theta=1-\sin ^{2} \theta \\
\tan ^{2} \theta=\sec ^{2} \theta-1 \\
\cot ^{2} \theta=\csc ^{2} \theta-1
\end{array}
\]

At the beginning of this chapter, we discussed verifying trigonometric identities. Now that we have some basic identities to work with, let's use them to verify the equality of some more complicated statements. The process of verifying trigonometric identities involves changing one side of the given expression into the other side. since these are not really equations, we will not treat them the way we treat equations. That is to say, we won't add or subtract anything to both sides of the statement (or multiply or divide by anything on both sides either).

Another reason for not treating a trigonometric identity as an equation is that, in practice, this process typically involves just one side of the statement. In problem solving, mathematicians typically use trigonometric identities to change the appearance of a problem without changing its value. In this process, a trigonometric expression is changed into another trigonometric expression rather than showing that two trigonometric expressions are the same, which is what we will be doing.

Example 1
Verify the identity \((\sin \theta)(\cot \theta)=\cos \theta\)
This is a very straightforward identity and it can solved by using one of the fundamental approaches to working with trigonometric identities. This is the approach of writing everything in terms of sines and cosines.

Beginning with the original statement:
\[ (\sin \theta)(\cot \theta)=\cos \theta
\] Replace \(\cot \theta\) with \(\frac{\cos \theta}{\sin \theta}\)
\[ (\sin \theta) \frac{\cos \theta}{\sin \theta}=\cos \theta
\] Then canceling out the \(\sin \theta:\)
\[ \cos \theta=\cos \theta
\]

There are four fundamental approaches to verifying trigonometric identities:
1. write everything in terms of sines and cosines
2. make a common denominator and add fractions
3. split a fraction
4. factor and cancel
Not all of these can be used in every problem and some problems will use combinations of these strategies. Here is another example.

Example 2
Verify the identity \(\tan \theta+\cot \theta=\sec \theta \csc \theta\)
First we'll write everything in terms of sines and cosines:
\[ \begin{array}{l}
\tan \theta+\cot \theta=\sec \theta \csc \theta \\
\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\sin \theta}=\frac{1}{\cos \theta} \cdot \frac{1}{\sin \theta}
\end{array}
\]

Next, on the left hand side, we can add the two fractions together by making a common denominator of \(\cos \theta \sin \theta\)
\begin{aligned}
\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\sin \theta} &=\frac{1}{\cos \theta} \cdot \frac{1}{\sin \theta} \\
\frac{\sin \theta}{\sin \theta} \cdot \frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\sin \theta} \cdot \frac{\cos \theta}{\cos \theta} &=\frac{1}{\cos \theta} \cdot \frac{1}{\sin \theta} \\
\frac{\sin ^{2} \theta}{\sin \theta \cos \theta}+\frac{\cos ^{2} \theta}{\sin \theta \cos \theta} &=\frac{1}{\cos \theta} \cdot \frac{1}{\sin \theta} \\
\frac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin \theta \cos \theta} &=\frac{1}{\cos \theta} \cdot \frac{1}{\sin \theta} \\
\frac{1}{\sin \theta \cos \theta} &=\frac{1}{\sin \theta \cos \theta}
\end{aligned}

In this example, you can see that we have first written everything in terms of sines and cosines, then created common denominators and added the fractions on the left hand side together. After this is done, we can replace the expression \(\sin ^{2} \theta+\cos ^{2} \theta\) with \(1,\) since this is the fundamental Pythagorean Identity.

Example 3
Verify the identity \(\frac{\tan \theta-\cot \theta}{\sin \theta \cos \theta}=\sec ^{2} \theta-\csc ^{2} \theta\)
We'll begin this problem by splitting the fraction over the denominator. This can be helpful in problems in which there is no addition or subtraction in the denominator. The idea here is that since \(\frac{a}{x}+\frac{b}{x}=\frac{a+b}{x},\) then we can reverse this process and say that \(\frac{a+b}{x}=\frac{a}{x}+\frac{b}{x}\)
In the problem above we'll say that:

\[\frac{\tan \theta-\cot \theta}{\sin \theta \cos \theta}=\sec ^{2} \theta-\csc ^{2} \theta\] \[\frac{\tan \theta}{\sin \theta \cos \theta}-\frac{\cot \theta}{\sin \theta \cos \theta}=\sec ^{2} \theta-\csc ^{2} \theta\] \[\frac{\frac{\sin \theta}{\cos \theta}}{\sin \theta \cos \theta}-\frac{\frac{\cos \theta}{\sin \theta}}{\sin \theta \cos \theta}=\sec ^{2} \theta-\csc ^{2} \theta\] \[\frac{\sin \theta}{\cos \theta} \cdot \frac{1}{\sin \theta \cos \theta}-\frac{\cos \theta}{\sin \theta} \cdot \frac{1}{\sin \theta \cos \theta}=\sec ^{2} \theta-\csc ^{2} \theta\] \[\frac{\cancel{\sin \theta}}{\cos \theta} \cdot \frac{1}{\cancel{\sin \theta} \cos \theta}-\frac{\cancel{\cos \theta}}{\sin \theta} \cdot \frac{1}{\sin \theta \cancel{\cos \theta}}=\sec ^{2} \theta-\csc ^{2} \theta\] \[\frac{1}{\cos ^{2} \theta}-\frac{1}{\sin ^{2} \theta}=\sec ^{2} \theta-\csc ^{2} \theta\] \[ \sec ^{2} \theta-\csc ^{2} \theta=\sec ^{2} \theta-\csc ^{2} \theta
\]

Example 4
Verify the identity \(\frac{\tan ^{2} \theta-\cos ^{2} \theta}{1-\cos ^{2} \theta}=\sec ^{2} \theta-\cot ^{2} \theta\)
On the left-hand side, notice the expression \(1-\cos ^{2} \theta\) in the denominator. We can replace this with \(\sin ^{2} \theta,\) which is a simpler expression. It is often helpful to have a simpler expression in the denominator rather than a more complicated expression.

\[ \begin{array}{l}
\frac{\tan ^{2} \theta-\cos ^{2} \theta}{1-\cos ^{2} \theta}=\sec ^{2} \theta-\cot ^{2} \theta \\
\frac{\tan ^{2} \theta-\cos ^{2} \theta}{\sin ^{2} \theta}=\sec ^{2} \theta-\cot ^{2} \theta
\end{array}
\] Next, we can split the fraction over the denominator of \(\sin ^{2} \theta\)
\[ \frac{\tan ^{2} \theta-\cos ^{2} \theta}{\sin ^{2} \theta}=\sec ^{2} \theta-\cot ^{2} \theta
\] \[ \frac{\tan ^{2} \theta}{\sin ^{2} \theta}-\frac{\cos ^{2} \theta}{\sin ^{2} \theta}=\sec ^{2} \theta-\cot ^{2} \theta
\]

We can see on the left-hand side that the expression \(\frac{\cos ^{2} \theta}{\sin ^{2} \theta}\) is equivalent to \(\cot ^{2} \theta\) but the first piece on the left-hand side needs to be simplified a little more. We'll rewrite \(\tan ^{2} \theta\) as \(\frac{\sin ^{2} \theta}{\cos ^{2} \theta}\) and then simplify the complex fraction.
\[ \begin{array}{c}
\frac{\tan ^{2} \theta}{\sin ^{2} \theta}-\frac{\cos ^{2} \theta}{\sin ^{2} \theta}=\sec ^{2} \theta-\cot ^{2} \theta \\
\frac{\frac{\sin ^{2} \theta}{\cos ^{2} \theta}}{\sin ^{2} \theta}-\cot ^{2} \theta=\sec ^{2} \theta-\cot ^{2} \theta \\

\frac{\sin ^{2} \theta}{\cos ^{2} \theta} \cdot \frac{1}{\sin ^{2} \theta}-\cot ^{2} \theta=\sec ^{2} \theta-\cot ^{2} \theta \\
\frac{\cancel{\sin ^{2} \theta}}{\cos ^{2} \theta} \cdot \frac{1}{\cancel{\sin ^{2} \theta}}-\cot ^{2} \theta=\sec ^{2} \theta-\cot ^{2} \theta
\end{array}
\]

After we cancel out the \(\sin ^{2} \theta,\) we're almost done:
\[ \begin{aligned}
\frac{\cancel{\sin ^{2} \theta}}{\cos ^{2} \theta} \cdot \frac{1}{\cancel{\sin ^{2} \theta}}-\cot ^{2} \theta &=\sec ^{2} \theta-\cot ^{2} \theta \\
& \frac{1}{\cos ^{2} \theta}-\cot ^{2} \theta=\sec ^{2} \theta-\cot ^{2} \theta \\
& \sec ^{2} \theta-\cot ^{2} \theta=\sec ^{2} \theta-\cot ^{2} \theta
\end{aligned}
\] The trigonometric identities we have discussed in this section are summarized below:

In the examples above and in the exercises, the form sin \(\theta\) or \(\cos \theta\) is typically used, however any letter may be used to represent the angle in question so long as it is the SAME letter in all expressions. For example, we can say that:
\[ \sin ^{2} \theta+\cos ^{2} \theta=1
\] or we can say that

\[ \sin ^{2} x+\cos ^{2} x=1
\] however:
\[ \sin ^{2} \theta+\cos ^{2} x \neq 1
\] because \(\theta\) and \(x\) could be different angles!

Exercises 3.1
In each problem verify the given trigonometric identify.

1. \(\cos \theta(\sec \theta-\cos \theta) = \sin ^{2} \theta\\[4pt] \)

2. \(\tan \theta(\cot \theta+\tan \theta) = \sec ^{2} \theta\\[4pt] \)

3. \(\tan \theta(\csc \theta+\cot \theta)-\sec \theta = 1\\[4pt] \)

4. \(\cot \theta(\sec \theta+\tan \theta)-\csc \theta = 1\\[4pt] \)

5. \(\tan ^{2} \theta \csc ^{2} \theta-\tan ^{2} \theta = 1\\[4pt] \)

6. \( \sin ^{2} \theta \cot ^{2} \theta+\sin ^{2} \theta = 1\\[4pt] \)

7. \(\dfrac{\sin \theta \tan \theta+\sin \theta}{\tan \theta+\tan ^{2} \theta} = \cos \theta\\[4pt] \)

8. \(\dfrac{\cos \theta \cot \theta+\cos \theta}{\cot \theta+\cot ^{2} \theta} = \sin \theta\\[4pt] \)

9. \(\dfrac{(\sin \theta+\cos \theta)^{2}}{\cos \theta}-\sec \theta=2 \sin \theta\\[4pt] \)

10. \( ( \sin \theta+\cos \theta)^{2}+(\sin \theta-\cos \theta)^{2} = 2\\[4pt] \)

11. \(\cos \theta(\tan \theta+\cot \theta) = \csc \theta\\[4pt] \)

12. \(\sin \theta(\cot \theta+\tan \theta) = \sec \theta\\[4pt] \)

13. \(\dfrac{\cos \theta}{\tan \theta}-\csc \theta = -\sin \theta\\[4pt] \)

14. \(\dfrac{\sin \theta}{\cot \theta}-\sec \theta = -\cos \theta\\[4pt] \)

15. \(\dfrac{\csc \theta}{\cos \theta}-\dfrac{\cos \theta}{\csc \theta} = \dfrac{\cot ^{2} \theta+\sin ^{2} \theta}{\cot \theta}\\[4pt] \)

16. \(\dfrac{\sec \theta+\csc \theta}{\tan \theta+\cot \theta} = \sin \theta+\cos \theta\\[4pt] \)

17. \(\dfrac{\sin \theta}{1+\sin \theta}-\dfrac{\sin \theta}{1-\sin \theta} = -2 \tan ^{2} \theta\\[4pt] \)

18. \(\dfrac{\cos \theta}{1+\cos \theta}-\dfrac{\cos \theta}{1-\cos \theta} = -2 \cot ^{2} \theta\\[4pt] \)

19. \(\dfrac{\cot \theta}{1+\csc \theta}-\dfrac{\cot \theta}{1-\csc \theta} = 2 \sec \theta\\[4pt] \)  

20. \(\dfrac{\tan \theta}{1+\sec \theta}-\dfrac{\tan \theta}{1-\sec \theta} = 2 \csc \theta\\[4pt] \)

21. \(\dfrac{\sec ^{2} \theta}{1+\cot ^{2} \theta} = \tan ^{2} \theta\\[4pt] \)

22. \(\dfrac{\csc ^{2} \theta}{1+\tan ^{2} \theta} = \cot ^{2} \theta\\[4pt] \)

23. \(\sec ^{4} \theta-\sec ^{2} \theta = \tan ^{4} \theta+\tan ^{2} \theta\\[4pt] \)

24. \(\csc ^{4} \theta-\csc ^{2} \theta = \cot ^{4} \theta+\cot ^{2} \theta\\[4pt] \)

25. \(1-\dfrac{\cos ^{2} \theta}{1+\sin \theta} = \sin \theta\\[4pt] \)

26. \(1-\dfrac{\sin ^{2} \theta}{1+\cos \theta} = \cos \theta\\[4pt] \)

27. \(\dfrac{\sec \theta}{\csc \theta} + \dfrac{\sin \theta}{\cos \theta} = 2 \tan \theta\\[4pt] \)

28. \(\dfrac{1-\sin \theta}{\cos \theta}+\dfrac{\cos \theta}{1-\sin \theta} = 2 \sec \theta\\[4pt] \)

29. \(\dfrac{\cos \theta}{1+\sin \theta}+\dfrac{1+\sin \theta}{\cos \theta} = 2 \sec \theta\\[4pt] \)

30. \(\dfrac{\tan \theta-\cot \theta}{\tan \theta+\cot \theta} = \sin ^{2} \theta-\cos ^{2} \theta\\[4pt] \)

31. \(\dfrac{\sec \theta-\cos \theta}{\sec \theta+\cos \theta} = \dfrac{\sin ^{2} \theta}{1+\cos ^{2} \theta}\\[4pt] \)

32. \(\dfrac{\sec \theta+\tan \theta}{\cot \theta+\cos \theta} = \tan \theta \sec \theta\\[4pt] \)