10.2: Double-Angle Identities

In this section we will include several new identities to the collection we established in the previous section. These new identities are called "Double-Angle Identities \(^{\prime \prime}\) because they typically deal with relationships between trigonometric functions of a particular angle and functions of "two times" or double the original angle.

To establish the validity of these identities we need to use what are known as the Sum and Difference Identities. These are identities that deal with expressions such as \(\sin (\alpha+\beta) .\) First we will establish an expression that is equivalent to \(\cos (\alpha-\beta)\)
Let's start with the unit circle:

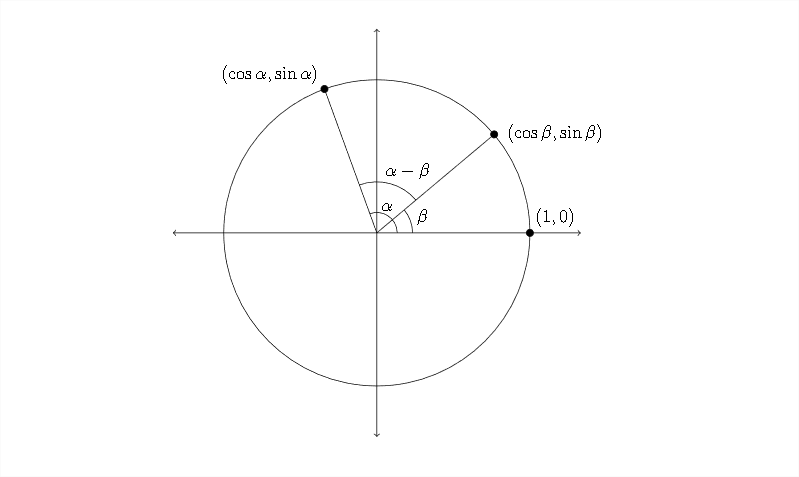
If we rotate everything in this picture clockwise so that the point labeled \((\cos \beta, \sin \beta)\) slides down to the point labeled \((1,0),\) then the angle of rotation in the diagram will be \(\alpha-\beta\) and the corresponding point on the edge of the circle will be:
\((\cos (\alpha-\beta), \sin (\alpha-\beta))\)
The diagram that represents this rotation is on the next page.

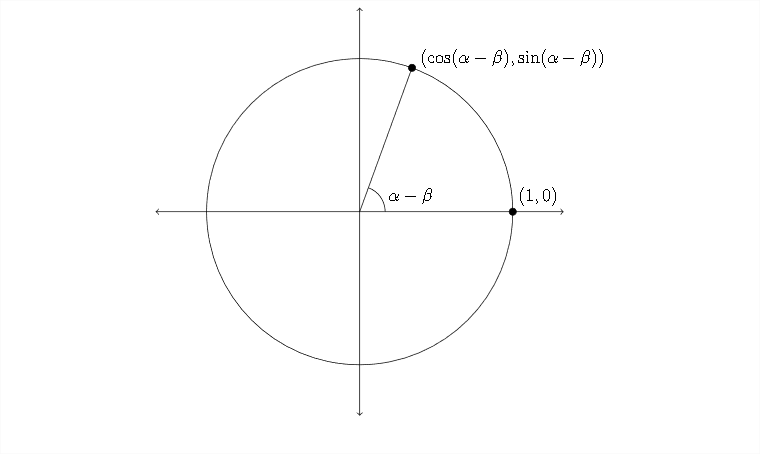
since the the second diagram is created by rotating the lines and points from the first diagram, the distance between the points \((\cos \alpha, \sin \alpha)\) and \((\cos \beta, \sin \beta)\) in the first diagram is the same as the distance between \((\cos (\alpha-\beta), \sin (\alpha-\beta))\) and the point (1,0) in the second diagram.

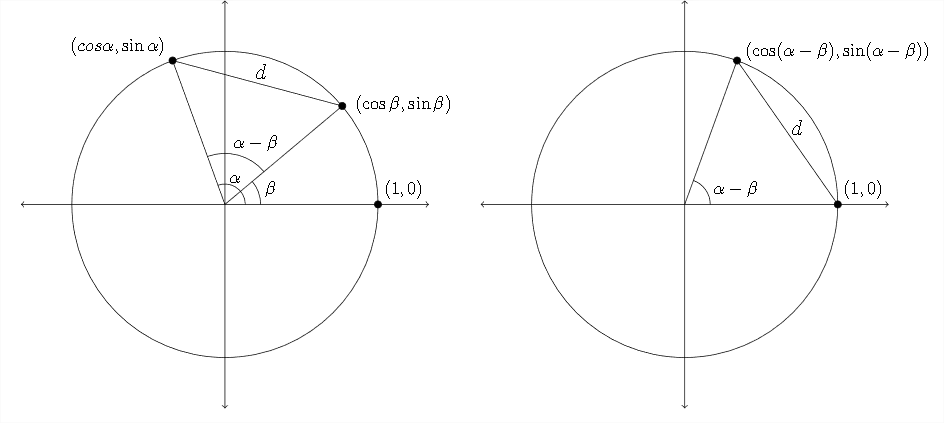
In the diagram above the length of \(d\) in each picture is the same.

We can represent this distance \(d\) with the distance formula used to calculate the distance between two points in the coordinate plane:
The distance between the points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is
\[ d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}
\] So, in the first diagram the distance \(d\) will be:
\[ d=\sqrt{(\cos \alpha-\cos \beta)^{2}+(\sin \alpha-\sin \beta)^{2}}
\]

In the second diagram the distance \(d\) will be:
\[ d=\sqrt{(\cos (\alpha-\beta)-1)^{2}+(\sin (\alpha-\beta)-0)^{2}}
\] since these distances are the same, we can set them equal to each other:
\[ \sqrt{(\cos \alpha-\cos \beta)^{2}+(\sin \alpha-\sin \beta)^{2}}=\sqrt{(\cos (\alpha-\beta)-1)^{2}+(\sin (\alpha-\beta)-0)^{2}}
\] We'll square both sides to clear the radicals:
\[ (\cos \alpha-\cos \beta)^{2}+(\sin \alpha-\sin \beta)^{2}=(\cos (\alpha-\beta)-1)^{2}+(\sin (\alpha-\beta)-0)^{2}
\] Next, we'll rewrite \((\sin (\alpha-\beta)-0)^{2}\) as \(\sin ^{2}(\alpha-\beta)\)
\[ (\cos \alpha-\cos \beta)^{2}+(\sin \alpha-\sin \beta)^{2}=(\cos (\alpha-\beta)-1)^{2}+\sin ^{2}(\alpha-\beta)
\]

Now we'll work to simplify the expressions on the left-hand side of this equation.
\[ (\cos \alpha-\cos \beta)^{2}+(\sin \alpha-\sin \beta)^{2}=(\cos (\alpha-\beta)-1)^{2}+\sin ^{2}(\alpha-\beta)
\] First, each one needs to be squared:
\[ \begin{array}{l}
(\cos \alpha-\cos \beta)^{2}=\cos ^{2} \alpha-2 \cos \alpha \cos \beta+\cos ^{2} \beta \\
(\sin \alpha-\sin \beta)^{2}=\sin ^{2} \alpha-2 \sin \alpha \sin \beta+\sin ^{2} \beta
\end{array}
\] So, the left-hand side will now be:
\[ \cos ^{2} \alpha-2 \cos \alpha \cos \beta+\cos ^{2} \beta+\sin ^{2} \alpha-2 \sin \alpha \sin \beta+\sin ^{2} \beta
\]

If we rearrange this a little, it will simplify nicely:
\[ \begin{array}{l}
\cos ^{2} \alpha-2 \cos \alpha \cos \beta+\cos ^{2} \beta+\sin ^{2} \alpha-2 \sin \alpha \sin \beta+\sin ^{2} \beta \\
\sin ^{2} \alpha+\cos ^{2} \alpha+\sin ^{2} \beta+\cos ^{2} \beta-2 \cos \alpha \cos \beta-2 \sin \alpha \sin \beta
\end{array}
\] Notice the Pythagorean Identities at the front of this expression - these are each equal to 1:
\[ \begin{array}{c}
\sin ^{2} \alpha+\cos ^{2} \alpha+\sin ^{2} \beta+\cos ^{2} \beta-2 \cos \alpha \cos \beta-2 \sin \alpha \sin \beta \\
1+1-2 \cos \alpha \cos \beta-2 \sin \alpha \sin \beta \\
2-2 \cos \alpha \cos \beta-2 \sin \alpha \sin \beta \\
2(1-\cos \alpha \cos \beta-\sin \alpha \sin \beta)
\end{array}
\]

Now that we've simplified the left-hand side, we'll simplify the right-hand side First we'll square the expression \((\cos (\alpha-\beta)-1)^{2}\)
\[ (\cos (\alpha-\beta)-1)^{2}=\cos ^{2}(\alpha-\beta)-2 \cos (\alpha-\beta)+1
\] So, the right-hand side is now:
\[ \cos ^{2}(\alpha-\beta)-2 \cos (\alpha-\beta)+1+\sin ^{2}(\alpha-\beta)
\] If we rearrange this expression, we'll again have a nice Pythagorean Identity:
\[ \begin{array}{c}
\sin ^{2}(\alpha-\beta)+\cos ^{2}(\alpha-\beta)-2 \cos (\alpha-\beta)+1 \\
1-2 \cos (\alpha-\beta)+1 \\
2-2 \cos (\alpha-\beta) \\
2(1-\cos (\alpha-\beta))
\end{array}
\]

So the left-hand side was equal to:
\[ 2(1-\cos \alpha \cos \beta-\sin \alpha \sin \beta)
\] And the right-hand side was equal to:
\[ 2(1-\cos (\alpha-\beta))
\] So, our original statement in simplified form is:
\[ 2(1-\cos \alpha \cos \beta-\sin \alpha \sin \beta)=2(1-\cos (\alpha-\beta))
\]

If we divide by 2 on both sides, we'll have:
\[ 1-\cos \alpha \cos \beta-\sin \alpha \sin \beta=1-\cos (\alpha-\beta)
\] then subtract 1
\[ -\cos \alpha \cos \beta-\sin \alpha \sin \beta=-\cos (\alpha-\beta)
\] and multiply through by -1
\[ \begin{array}{r}
\cos \alpha \cos \beta+\sin \alpha \sin \beta=\cos (\alpha-\beta) \\
\mathrm{So}, \cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta
\end{array}
\] This will help us to generate the double-angle formulas, but to do this, we don't want \(\cos (\alpha-\beta),\) we want \(\cos (\alpha+\beta)\) (you'll see why in a minute).

So, to change this around, we'll use identities for negative angles. Recall that in the fourth quadrant the sine function is negative and the cosine function is positive. For this reason, \(\sin (-\theta)=-\sin (\theta)\) and \(\cos (-\theta)=\cos (\theta)\)
Now we can say that \(\cos (2 \theta)=\cos (\theta+\theta)=\cos (\theta-(-\theta)) .\) Going back to our
identity for \(\cos (\alpha-\beta),\) we can say that:

\[ \begin{aligned}
\cos (\theta-(-\theta)) &=\cos \theta \cos (-\theta)+\sin \theta \sin (-\theta) \\
\cos (\theta-(-\theta)) &=\cos \theta \cos \theta+\sin \theta(-\sin \theta) \\
\cos (\theta-(-\theta)) &=\cos \theta \cos \theta-\sin \theta \sin \theta \\
\cos (\theta-(-\theta)) &=\cos ^{2} \theta-\sin ^{2} \theta \\
\cos (\theta+\theta) &=\cos ^{2} \theta-\sin ^{2} \theta \\
\cos (2 \theta) &=\cos ^{2} \theta-\sin ^{2} \theta
\end{aligned}
\] This is the double-angle identity for the cosine: \(\quad \cos (2 \theta)=\cos ^{2} \theta-\sin ^{2} \theta\)

This identity actually appears in any one of three forms because the Pythagorean Identities can be applied to this to change its appearance:
\[ \begin{array}{l}
\cos (2 \theta)=\cos ^{2} \theta-\sin ^{2} \theta \\
\cos (2 \theta)=1-\sin ^{2} \theta-\sin ^{2} \theta \\
\cos (2 \theta)=1-2 \sin ^{2} \theta
\end{array}
\] If we substitute for the \(\sin ^{2} \theta\) term:
\[ \begin{array}{l}
\cos (2 \theta)=\cos ^{2} \theta-\sin ^{2} \theta \\
\cos (2 \theta)=\cos ^{2} \theta-\left(1-\cos ^{2} \theta\right) \\
\cos (2 \theta)=\cos ^{2} \theta-1+\cos ^{2} \theta \\
\cos (2 \theta)=2 \cos ^{2} \theta-1
\end{array}
\]

So, the three forms of the cosine double angle identity are:
\[ \begin{aligned}
\cos (2 \theta) &=\cos ^{2} \theta-\sin ^{2} \theta \\
&=2 \cos ^{2} \theta-1 \\
&=1-2 \sin ^{2} \theta
\end{aligned}
\] The double-angle identity for the sine function uses what is known as the cofunction identity. Remember that, in a right triangle, the sine of one angle is the same as the cosine of its complement (which is the other acute angle). This is because the adjacent side for one angle is the opposite side for the other angle. The denominator in both cases is the hypotenuse, so the cofunctions of complementary angles are equal.

In the diagram below, we can see this more clearly:

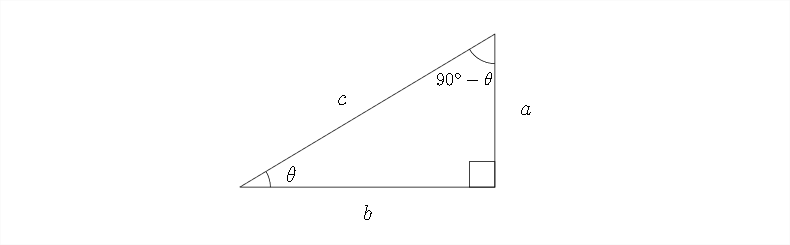
In the diagram above note that:
\[ \sin \theta=\frac{a}{c}=\cos \left(90^{\circ}-\theta\right)
\] So, if we want an identity for \(\sin (\theta+\theta),\) we'll start with \(\sin (\alpha+\beta)\) which is equivalent to \(\cos \left(90^{\circ}-(\alpha+\beta)\right) .\) We'll use a trick here and restate this as:
\[ \begin{aligned}
\sin (\alpha+\beta) &=\cos \left(90^{\circ}-(\alpha+\beta)\right) \\
&=\cos \left(90^{\circ}-\alpha-\beta\right) \\
&=\cos \left(\left(90^{\circ}-\alpha\right)-\beta\right) \\
&=\cos \left(90^{\circ}-\alpha\right) \cos \beta+\sin \left(90^{\circ}-\alpha\right) \sin \beta \\
&=\sin \alpha \cos \beta+\cos \alpha \sin \beta
\end{aligned}
\]

Now, we can use this to find an expression for \(\sin 2 \theta=\sin (\theta+\theta)\)
\[ \begin{aligned}
\sin 2 \theta &=\sin (\theta+\theta) \\
&=\sin \theta \cos \theta+\cos \theta \sin \theta \\
&=2 \sin \theta \cos \theta
\end{aligned}
\]

Exercises 3.2

Here is a summary of all the identities we've worked with in this chapter:

Pythagorean Identities
\(\sin ^{2} \theta+\cos ^{2} \theta=1\)
\(\tan ^{2} \theta+1=\sec ^{2} \theta\)
\(1+\cot ^{2} \theta=\csc ^{2} \theta\)

Reciprocal Identities
\(\tan \theta=\frac{\sin \theta}{\cos \theta}\)
\(\cot \theta=\frac{\cos \theta}{\sin \theta}\)
\(\sec \theta=\frac{1}{\cos \theta}\)
\(\csc \theta=\frac{1}{\sin \theta}\)

Double-Angle Identities
\(\cos (2 \theta)=\cos ^{2} \theta-\sin ^{2} \theta\)
\(\cos (2 \theta)=2 \cos ^{2} \theta-1\)
\(\cos (2 \theta)=1-2 \sin ^{2} \theta\)
\(\sin (2 \theta)=2 \sin \theta \cos \theta\)

Working problems involving double-angle identities is very similar to the other identities we've worked with previously- you just have more identities to choose from!

Example
Verify the given identity: \(\cos 2 x=\frac{1-\tan ^{2} x}{1+\tan ^{2} x}\)
We have three possible identities to choose from for the left-hand side, so we'll wait on that for a moment while we simplify the right-hand side.

\[ \begin{aligned}
\frac{1-\tan ^{2} x}{1+\tan ^{2} x} &=\frac{1-\tan ^{2} x}{\sec ^{2} x} \\
&=\frac{1}{\sec ^{2} x}-\frac{\tan ^{2} x}{\sec ^{2} x} \\
&=\cos ^{2} x-\frac{\left(\frac{\sin ^{2} x}{\cos ^{2} x}\right)}{\left(\frac{1}{\cos ^{2} x}\right)} \\
&=\cos ^{2} x-\frac{\sin ^{2} x}{\cos ^{2} x} \cdot \frac{\cos ^{2} x}{1} \\
&=\cos ^{2} x-\frac{\sin ^{2} x}{\cancel{\cos ^{2} x}} \cdot \frac{\cancel{\cos ^{2} x}}{1} \\
&=\cos ^{2} x-\sin ^{2} x
\end{aligned}
\] This is one of the identities for \(\cos (2 \theta)\) so we can stop and simply state \(\cos (2 x)=\) \(\cos ^{2} x-\sin ^{2} x\)

In each problem verify the given trigonometric identity.
1. \(\frac{2 \sin x \cos x}{\cos ^{2} x-\sin ^{2} x}=\tan (2 x)\)
2. \(\sec (2 x)=\frac{\sec ^{2} x}{2-\sec ^{2} x}\)
3. \(\sin (2 x) \csc x=2 \cos x\)
4. \(\frac{2 \cos x}{\sin (2 x)}=\csc x\)
5. \(\frac{\cos (2 x)}{\sin x}+\sin x=\frac{\cot x}{\sec x}\)
6. \(\frac{\sin x+\sin (2 x)}{\sec x+2}=\sin x \cos x\)
7. \((\sin x+\cos x)^{2}=1+\sin (2 x)\)
8. \(\left(\sin ^{2} x-1\right)^{2}=\sin ^{4} x+\cos (2 x)\)
9. \(2 \cos x-\frac{\cos (2 x)}{\cos x}=\sec x\)
10. \(\frac{1+\cos (2 x)}{1-\cos (2 x)}=\cot ^{2} x\)
11. \(\frac{\cos (2 x)}{\sin ^{2} x}=\cot ^{2} x-1\)
12. \(\frac{\cos (2 x)}{\sin ^{2} x}=\csc ^{2} x-2\)
13. \(\frac{\cot x-\tan x}{\cot x+\tan x}=\cos 2 x\)
14. \(\sin 2 x=\frac{2(\tan x-\cot x)}{\tan ^{2} x-\cot ^{2} x}\)
15. \(\frac{2 \cos 2 x}{\sin 2 x}=\cot x-\tan x\)
16. \(\tan 2 x=\frac{2}{\cot x-\tan x}\)
17. \(\frac{\sin x}{1+\cos x}+\frac{1+\cos x}{\sin x}=2 \csc x\)
18. \(\tan x+\cot x=2 \csc (2 x)\)
19. \(\cos (2 x)=\frac{\cot ^{2} x-1}{\cot ^{2} x+1}\)
20. \(\sin (2 x)=\frac{2 \tan x}{1+\tan ^{2} x}\)
21. \(\frac{2 \sin ^{2} x}{\sin (2 x)}+\cot x=\sec x \csc x\)
22. \(\sec ^{2} x \cos (2 x)=\sec ^{2} x-2 \tan ^{2} x\)
23. \(\frac{\cos (2 x)}{\sin x}+\sin x=\csc x-\sin x \quad\)
24. \(\frac{2 \tan x-\sin (2 x)}{2 \sin ^{2} x}=\tan x\)