1.1: An Introduction to the Integers
- Page ID
- 19849
We begin with the set of counting numbers, formally called the set of natural numbers.
The Natural Numbers
The set \[\mathbb{N}=\{1,2,3,4,5, \ldots \} \nonumber \] is called the set of natural numbers.
If we add the number zero to the set of natural numbers, then we have a set of numbers that are called the whole numbers.
The Whole Numbers
The set \[W=\{0,1,2,3,4,5, \ldots\} \nonumber \] is called the set of whole numbers.
The number \(0\) is special, in that whenever you add it to another whole number, you get the identical number as an answer.
Additive Identity Property
If a is any whole number, then \[a +0=a \nonumber \] For this reason, the whole number \(0\) is called the additive identity.
Thus, for example, \(3 + 0 = 3\), \(15 + 0 = 15\), and \(123 + 0 = 123\). These are all examples of the additive identity property. Every natural number has an opposite, so that when you add them together, their sum is zero.
Additive Inverse Property
If \(a\) is any natural number, then define the opposite of \(a\), symbolized by \(-a\), so that \[a +(-a)=0 \nonumber \] The number \(-a\) is called the “opposite of \(a\),” or more formally, the additive inverse of \(a\).
For example, the opposite (additive inverse) of \(3\) is \(−3\), and \(3+(−3) = 0\). The opposite (additive inverse) of \(12\) is \(−12\), and \(12 + (−12) = 0\). The opposite of \(254\) is \(−254\), and \(254+(−254) = 0\). These are all examples of additive inverses and the additive inverse property.
Because \(7+(−7) = 0\), we’ve said that \(−7\) is the opposite (additive inverse) of \(7\). However, we can also turn that around and say that \(7\) is the opposite of \(−7\). If we translate the phrase “the opposite of \(−7\) is \(7\)” into mathematical symbols, we get \(−(−7) = 7\).
The opposite of the opposite
Because \(a+(-a)=0,\) we can say that \(a\) is the opposite of \(-a\). In symbols, we write: \[-(-a)=a \nonumber \]
Thus, for example, \(-(-11)=11\), \(-(-103)=103\), and \(-(-1255)=1255\).
The Integers
If we collect all the natural numbers and their additive inverses, then include the number zero, we have a collection of numbers called the integers.
The Integers
The set \[\mathbb{Z}=\{\ldots,-5,-4,-3,-2,-1,0,1,2,3,4,5, \ldots\} \nonumber \] is called the set of integers.
The integers can be made to correspond to points on a line in a very natural manner. First, draw a line, then locate the number zero anywhere you wish. Secondly, place the number one to the right of zero. This determines the length of one unit. Finally, locate the numbers \(1,2,3,4,5, \dots\) to the right of zero, then their opposites (additive inverses) \(-1,-2,-3,-4,-5, \dots\) to the left of zero (see Figure \(\PageIndex{1}\)).
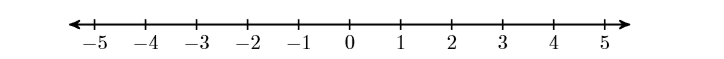
Figure \(\PageIndex{1}\): Each integer corresponds to a unique position on the number line.
Note that as we move to the right on the number line, the integers get larger. On the other hand, as we move to the left on the number line, the integers get smaller.
Positive and negative integers
On the number line, some integers lie to the right of zero and some lie to the left of zero.
- If \(a\) is an integer that lies to the right of zero, then \(a\) is called a positive integer.
- If \(a\) is an integer that lies to the left of zero, then \(a\) is called a negative integer.
Thus, \(4\), \(25\), and \(142\) are positive integers, while \(-7\), \(-53,\) and \(-435\) are negative integers.
Absolute Value
The absolute value (or magnitude) of an integer is defined as follows.
The Absolute Value of an Integer
If \(a\) is an integer, then the absolute value of \(a\), written \(|a|\), is defined as the distance between the integer and zero on the number line.
Example \(\PageIndex{1}\)
Simplify \(|-4|\).
Solution
Consider the position of \(-4\) on the number line. Note that \(-4\) lies four units away from zero.
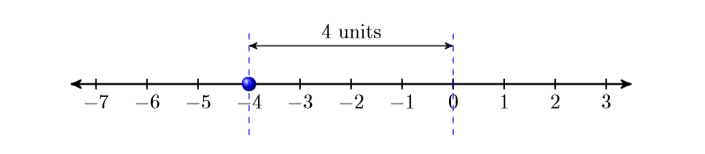
Figure \(\PageIndex{2}\)
Because the absolute value (magnitude) of an integer equals its distance from zero, \(|-4|=4\).
Exercise \(\PageIndex{1}\)
Simplify: \(|-23|\)
- Answer
-
\(|-23|=23\)
In similar fashion:
- The integer \(5\) lies five units away from zero. Hence, \(|5|= 5\).
- The integer \(0\) lies zero units away from zero, Hence, \(|0|= 0\). Note that the absolute value of any number is either positive or zero. That is, the absolute value of a number is nonnegative (not negative).
Integer Addition
This section is designed to provide a quick review of integer addition. We consider the first of two cases.
Adding Integers with Like Signs
To add two integers with like signs (both positive or both negative), add their magnitudes (absolute values), then prefix their common sign.
Example \(\PageIndex{2}\)
Simplify \(7+12\).
Solution
We have like signs. The magnitudes (absolute values) of \(7\) and \(12\) are \(7\) and \(12\), respectively. If we add the magnitudes, we get \(19\). If we prefix the common sign, we get \(19\). That is: \[7+12=19 \nonumber \]
Exercise \(\PageIndex{2}\)
Simplify: \(13+28\).
- Answer
-
\(41\)
Example \(\PageIndex{3}\)
Simplify \(-8+(-9)\).
Solution
We have like signs. The magnitudes (absolute values) of \(-8\) and \(-9\) are \(8\) and \(9\), respectively. If we add the magnitudes, we get \(17\). If we prefix the common sign, we get \(-17\). That is: \[-8+(-9)=-17 \nonumber \]
Exercise \(\PageIndex{3}\)
Simplify: \(-12+(-21)\).
- Answer
-
\(-33\)
Next, we consider the case where we have unlike signs.
Adding Integers with Unlike Signs
To add two integers with unlike signs (one positive and one negative), subtract the integer with the smaller magnitude (absolute value) from the number with the larger magnitude, then prefix the sign of the integer with the larger magnitude.
Example \(\PageIndex{4}\)
Simplify \(-14+11\).
Solution
We have unlike signs. The magnitudes (absolute values) of \(-14\) and \(11\) are \(14\) and \(11\), respectively. If we subtract the smaller magnitude from the larger, we get \(3\). The number \(-14\) has the larger magnitude, so we prefix our answer with its negative sign. That is: \[-14+11=-3 \nonumber \]
Exercise \(\PageIndex{4}\)
Simplify: \(12+(-29)\).
- Answer
-
\(-17\)
Example \(\PageIndex{5}\)
Simplify \(40+(-25)\).
Solution
We have unlike signs. The magnitudes (absolute values) of \(40\) and \(-25\) are \(40\) and \(25\), respectively. If we subtract the smaller magnitude from the larger, we get \(15\). The number \(40\) has the larger magnitude, so we prefix our answer with its positive sign. That is: \[40+(-25)=15 \nonumber \]
Exercise \(\PageIndex{5}\)
Simplify: \(32+(-90)\).
- Answer
-
\(-58\)
Mathematical Properties of Addition
The order in which we add integers does not matter. That is, \(-20 + 34\) gives an answer identical to the sum \(34 + (−20)\). In both cases, the answer is \(14\). This fact is called the commutative property of addition.
The Commutative Property of Addition
If \(a\) and \(b\) are any two integers, then: \[a+b=b+a \nonumber \]
Next, when we add three integers, it does not matter which two we add first. For example, if we add the second and third of three numbers first, we get:
\[\begin{aligned}-11+(-2+5) &=-11+3 \quad {\color{Red} \text { Parentheses first: }-2+5=3} \\ &=-8 \quad {\color{Red} \text { Add: }-11+3=-8} \end{aligned} \nonumber \]
On the other hand, if we add the first and second of three numbers first, we get:
\[\begin{aligned}(-11+(-2))+5 &=-13+5 \quad {\color{Red} \text { Parentheses first: }-11+(-2)=-13} \\ &=-8 \quad {\color{Red} \text { Add: }-13+5=-8} \end{aligned} \nonumber \]
Thus, \(-11 + (−2 + 5) = (−11 + (−2)) + 5\). This fact is called the associative property of addition.
The Associative Property of Addition
If \(a\), \(b\), and \(c\) are any three integers, then: \[a +( b + c)=( a + b)+c \nonumber \]
Integer Subtraction
Subtraction is the inverse, or the opposite, of addition.
Subtracting Integers
If \(a\) and \(b\) are any two integers, then: \[a-b = a +(-b) \nonumber \] Subtracting \(b\) is identical to adding the opposite (additive inverse) of \(b\).
Example \(\PageIndex{6}\)
Simplify: \(-13-27\).
Solution
The “opposite” (additive inverse) of \(27\) is \(-27\). So, subtracting \(27\) is the same as adding \(-27\).
\(\begin{aligned}-13-27&=-13+(-27) \quad {\color{Red} \text { Subtracting 27 is the same as adding −27.}} \\ &=-50 \quad {\color{Red} \text { Add the magnitudes, then prefix the common negative sign.}} \end{aligned}\)
Exercise \(\PageIndex{6}\)
Simplify: \(-11-15\).
- Answer
-
\(-26\)
Example \(\PageIndex{7}\)
Simplify: \(-27-(-50)\).
Solution
The “opposite” (additive inverse) of \(-50\) is \(-(-50)\), or \(50\). So, subtracting \(-50\) is the same as adding \(50\).
\(\begin{aligned}-27-(-50)&=-27+50 \quad {\color{Red} \text { Subtracting -50 is the same as adding 50.}} \\&=23 \quad {\color{Red} \text { Subtract the smaller magnitude from the larger magnitude, then prefix the sign of the larger magnitude.}} \end{aligned}\)
Exercise \(\PageIndex{7}\)
Simplify: \(-18-(-54)\).
- Answer
-
\(36\)
Integer Multiplication
This section is designed to provide a quick review of multiplication and division of integers.
Like Signs
If \(a\) and \(b\) are integers with like signs (both positive or both negative), then the product \(ab\) and the quotient \(a/b\) are positive.
\[\begin{array}{ll}{(+)(+)=+} \quad {\text { or }} & {(+) /(+)=+} \\ {(-)(-)=+\quad \text { or }} & {(-) /(-)=+}\end{array} \nonumber \]
Example \(\PageIndex{8}\)
Simplify each of the following expressions:
- \((2)(3)\)
- \((-12)(-8)\)
- \(-14 /(-2)\)
Solution
When multiplying or dividing, like signs yield a positive result.
- \((2)(3)=6\)
- \((-12)(-8)=96\)
- \(-14 /(-2)=7\)
Exercise \(\PageIndex{8}\)
Simplify: \((-18)(-5)\).
- Answer
-
\(90\)
Unlike Signs
If \(a\) and \(b\) are integers with unlike signs (one positive and one negative), then the product \(ab\) and the quotient \(a/b\) are negative.
\[\begin{array}{ll}{(+)(-)=-} & {\text { or }}& {(+) /(-)=-} \\ {(-)(+)=-} & {\text { or }} & {(-) /(+)=-}\end{array} \nonumber \]
Example \(\PageIndex{9}\)
Simplify each of the following expressions:
- \((2)(-12)\)
- \((-9)(12)\)
- \(24/(-8)\)
Solution
When multiplying or dividing, unlike signs yield a negative result.
- \((2)(-12)=-24\)
- \((-9)(12)=-108\)
- \(24 /(-8)=-3\)
Exercise \(\PageIndex{9}\)
Simplify: \((-19)(3)\).
- Answer
-
\(-57\)
Mathematical Properties of Multiplication
The order in which we multiply integers does not matter. That is, \((-8)(5)\) gives an answer identical to \((5)(-8)\). In both cases, the answer is \(-40\). This fact is called the commutative property of multiplication.
The Commutative Property of Multiplication
If \(a\) and \(b\) are any two integers, then: \[a \cdot b=b+a \nonumber \]
Next, when we multiply three integers, it does not matter which two we multiply first. If we multiply the second and third of three numbers first, we get:
\[\begin{aligned}(-3)[(-4)(-5)] &=(-3)(20) & {\color{Red} \text { Brackets first: }(-4)(-5)=20} \\ &=-60 & {\color{Red} \text { Multiply: }(-3)(20)=-60} \end{aligned} \nonumber \]
On the other hand, if we multiply the first and second of three numbers first, we get:
\[\begin{aligned}[(-3)(-4)](-5)&=(12)(-5) & {\color{Red} \text { Brackets first: }(-3)(-4)=12} \\ & =-60 & {\color{Red} \text { Multiply: }(12)(-5)=-60}\end{aligned} \nonumber \]
Thus, \((-3)[(-4)(-5)]=[(-3)(-4)](-5)\) . This fact is called the associative property of multiplication.
The Associative Property of Multiplication
If \(a\), \(b\), and \(c\) are any three integers, then: \[a \cdot(b \cdot c)=(a \cdot b) \cdot c \nonumber \]
When you multiply an integer by \(1\), you get the identical number back as the product. For example, \((1)(5) = 5\) and \((-11)(1) = -11\). This fact is known as the multiplicative identity property.
The Multiplicative Identity Property
If a is any integer, then: \[1 \cdot a=a \quad \text { and } \quad a \cdot 1=a \nonumber \] For this reason, the integer \(1\) is called the “multiplicative identity.”
Finally, note that \((-1)(5) = -5\). Thus, multiplying \(5\) by \(-1\) is identical to taking the “opposite” of \(5\) or negating \(5\).
The Multiplicative Property of \(−1\)
Multiplying by minus one is identical to negating. That is: \[(-1) a=-a \nonumber \]
Exponents
In the exponential expression \(a^n\), the number \(a\) is called the base, while the number \(n\) is called the exponent. We now define what is meant by an exponent.
Exponents
Let \(a\) be an integer and let \(n\) be any whole number. If \(n \neq 0\), then: \[a^{n}=\underbrace{a \cdot a \cdot a \cdot \cdots \cdot a}_{n \text { times }} \nonumber \]
That is, to calculate \(a^n\), write \(a\) as a factor \(n\) times.
Simplify \((-2)^{3}\).
Solution
In the exponential expression \((-2)^3\), note that \(-2\) is the base, while \(3\) is the exponent. The exponent tells us to write the base as a factor three times. Simplify the result by performing the multiplications in order, moving from left to right.
\[\begin{aligned}(-2)^{3} & =(-2)(-2)(-2)\quad {\color{Red}\text { -2 as a factor, three times.}} \\ & =(4)(-2)\quad {\color{Red}\text { Multiply: (-2)(-2)=4}} \\ & =-8 \quad {\color{Red}\text { Multiply: (4)(-2)=-8}}\\ \text{Thus } (-2)^{3} &=-8\end{aligned} \nonumber \]
Exercise \(\PageIndex{10}\)
Simplify: \((-2)^{2}\).
- Answer
-
\(4\)
In Example \(\PageIndex{10}\), note that the product of three negative factors is negative. Let’s try another example.
Simplify \((-2)^{4}\).
Solution
In the exponential expression \((-2)4\), note that \(-2\) is the base, while \(4\) is the exponent. The exponent tells us to write the base as a factor four times. Simplify the result by performing the multiplications in order, moving from left to right.
\[\begin{aligned}(-2)^{4} & =(-2)(-2)(-2)(-2)\quad {\color{Red}\text { -2 as a factor, four times.}} \\ & =(4)(-2)(-2)\quad {\color{Red}\text { Multiply: (-2)(-2)=4}} \\ & =(-8)(-2) \quad {\color{Red}\text { Multiply: (4)(-2)=-8}}\\ & = 16 \quad {\color{Red}\text { Multiply: (-8)(-2)=-8}}\\ \text{Thus } (-2)^{4} &=16\end{aligned} \nonumber \]
Exercise \(\PageIndex{11}\)
Simplify: \((-2)^{5}\).
- Answer
-
\(-32\)
In Example \(\PageIndex{11}\), note that the product of four negative factors is positive. Examples \(\PageIndex{10}\) and \(\PageIndex{11}\) reveal the following pattern.
Odd or Even Exponents
- When a negative integer is raised to an even exponent, the result is positive.
- When a negative integer is raised to an odd exponent, the result is negative.
Graphing Calculator: Negating versus Subtracting

Figure \(\PageIndex{3}\): Lower half of the TI-84.
Consider the view of the lower half of the TI-84 graphing calculator in Figure \(\PageIndex{3}\). Note that there are two keys that contain some sort of negative sign, one on the bottom row of keys, and another in the last column of keys on the right, positioned just above the plus symbol.
Figure \(\PageIndex{4}\)
The first of these buttons is the unary “negation” operator. If you want to negate a single (thus the word “unary”) number, then this is the key to use. For example, enter \(-3\) by pressing the following button sequence. The result is shown in Figure \(\PageIndex{7}\).

Figure \(\PageIndex{5}\)
The second button is the binary “subtraction” operator. If you want to subtract one number from another number (thus the word “binary”), then this is the key to use. For example, enter \(7-15\) by pressing the following button sequence. The result is shown in Figure \(\PageIndex{8}\).
Figure \(\PageIndex{6}\)
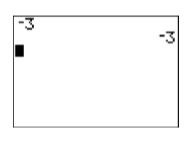
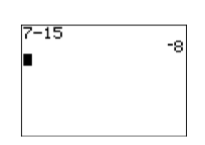
Figure \(\PageIndex{7}\): Negating a number. Figure \(\PageIndex{8}\): Subtract two numbers.
Note
Do not interchange the roles of the unary negation operator and the binary subtraction operator.
- To negate a number, use: (-)
- To subtract one number from another, use: −
If you interchange the roles of these operators, the calculator will respond that you’ve made a “syntax error” (see Figures \(\PageIndex{9}\) and \(\PageIndex{10}\) ).
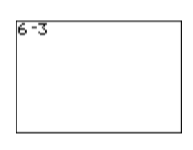

Figure \(\PageIndex{9}\): Using the wrong symbol for subtraction. Figure \(\PageIndex{10}\): The resulting syntax error.
Example \(\PageIndex{12}\)
Use the TI-84 graphing calculator to simplify each of the following expressons:
- \(-717-432\)
- \((232)(-313)\)
- \((-17)^{3}\)
Solution
The minus sign in each of these examples looks exactly the same, but sometimes it is used as a “negative” sign and sometimes it is used as a “subtraction” sign.
- The expression \(-717-432\) asks us to subtract \(432\) from “negative” \(717\). Enter the following sequence of keystrokes to produce the result shown in the first image in Figure \(\PageIndex{11}\).

Hence, \(-717-432=-1149\).
- The expression \((232)(-313)\) asks us to find the product of \(232\) and “negative” \(313\). Enter the following sequence of keystrokes to produce the result shown in the second image in Figure \(\PageIndex{11}\).
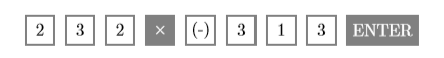
Hence, \((232)(-313)=-72616\).
- The expression \((-17)^3\) asks us to raise “negative” to the third power. Enter the following sequence of keystrokes to produce the result shown in the third image in Figure \(\PageIndex{11}\). The “caret” symbol ^ is located just above the division key in the rightmost column of the TI-84 graphing calculator.
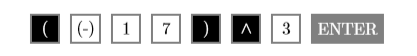
Hence, \((-17)^{3}=-4913\).
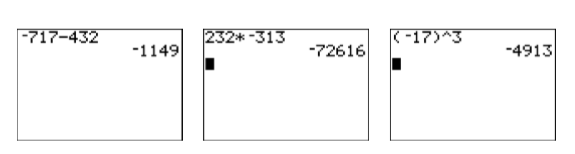
Figure \(\PageIndex{11}\): Calculations made on the graphing calculator.
Exercise \(\PageIndex{12}\)
Use the graphing calculator to evaluate \((-225)^3\).
- Answer
-
\((-225)^3 = -11390625\)
Contributors
David Arnold (Retired Professor (Mathematics) at College of the Redwoods)


