5.1: Functions

We begin with the definition of a relation.

Relation

A relation is a collection of ordered pairs.

The collection of ordered pairs \[R =\{(0,3),(0,4),(1,5),(2,6)\} \nonumber \] is an example of a relation.

If we collect the first element of each ordered pair in a set, we have what is called the domain of the relation.

Domain

The domain of a relation is the set of all first elements of the ordered pairs.

For example, in the relation \[R = \{(0,3),(0,4),(1,5),(2,6)\} \nonumber \]if we collect the first element of each ordered pair in \(R\), we get the domain: \[\text {Domain of R} = \{0,1,2\} \nonumber \]Although the number zero appears twice as a first element in the ordered pairs of \(R\), note that we list it only once when listing the elements in the domain of \(R\).

In similar fashion, if we collect the second elements of each ordered pair in a set, we have what is called the range of a relation.

Range

The range of a relation is the set of all second elements of the ordered pairs.

For example, in the relation \[R = \{(0,3),(0,4),(1,5),(2,6)\} \nonumber \]if we collect the second element of each ordered pair in \(R\), we get the range: \[\text {Range of R} = \{3,4,5,6\} \nonumber \]

Example \(\PageIndex{1}\)

State the domain and range of the relation \[T = \{(5,3),(6,3),(7,4)\} \nonumber \]

Solution

Collect the first element of each ordered pair in \(T\) to list the domain:

Domain of \(T=\{5,6,7\}\)

Collect the second element of each ordered pair in \(T\) to list the range:

Range of \(T=\{3,4\}\)

Note that even though the number three appears in the second position twice, we list it only once in describing the range.

Exercise \(\PageIndex{1}\)

State the domain and range of the relation \[S =\{(−1,7),(2,5),(2,3)\} \nonumber \]

Answer

Domain of \(S = \{−1,2\}\), Range of \(S = \{3,5,7\}\)

Example \(\PageIndex{2}\)

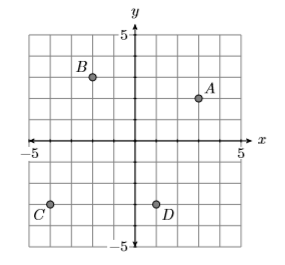
State the domain and range of the relation shown in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): We can present a relation as a collection of ordered pairs in a graph.

Solution

Point \(A\) has coordinates \((3,2)\), point \(B\) has coordinates \((−2,3)\), point \(C\) has coordinates \((−4,−3)\), and point \(D\) has coordinates \((1,−3)\). We can collect these points in a set. \[S = \{(3,2),(−2,3),(−4,−3),(1,−3)\} \nonumber \]

If we collect each element in the first position of each ordered pair, we have the domain.

Domain of \(S = \{−4,−2,1,3\}\)

Note that it is traditional to list the domain elements in order (smallest to largest). Next, if we collect each element in the second position of each ordered pair, we have the range.

Range of \(S = \{−3,2,3\}\)

Again, it is traditional to list the elements in order. Note again that we did not repeat the number \(−3\) in listing the range, even though it is used twice as a second element of an ordered pair in the set \(S\).

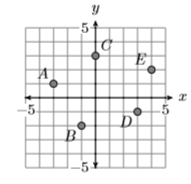
Exercise \(\PageIndex{2}\)

State the domain and range of the relation shown below.

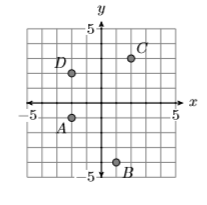
Answer

Domain of \(S =\{−2,1,2\}\), Range of \(S =\{−4,−1,2,3\}\)

Mapping Diagrams

A mapping diagram is a useful construction that helps one to analyze a relation. Consider the earlier relation \(R =\{(0,3),(0,4),(1,5),(2,6)\}\), which had domain \(\mathcal{D} = \{0,1,2\}\) and range \(\mathcal{R} = \{3,4,5,6\}\). To construct a mapping diagram for \(R\), list the elements in the domain of \(R\) on the left, list the elements of the range of \(R\) on the right, then use arrows to indicate the ordered pairs (see Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): Using a mapping diagram to describe the relation \(R\).

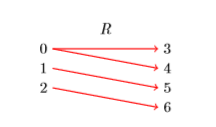
Note how the ordred pair \((0,3)\) is indicated by drawing an arrow connecting \(0\) on the left to \(3\) on the right. We say that the relation “maps \(0\) to \(3\)” and write \(R : 0 \rightarrow 3\). In similar fashion:

• The ordered pair \((0,4)\) is indicated by drawing an arrow connecting \(0\) on the left to \(4\) on the right; i.e., \(R\) “maps \(0\) to \(4\)” or \(R :0→ 4\).
• The ordered pair \((1,5)\) is indicated by drawing an arrow connecting \(1\) on the left to \(5\) on the right; i.e., \(R\) “maps \(1\) to \(5\)” or \(R :1→ 5\).
• The ordered pair \((2,6)\) is indicated by drawing an arrow connecting \(2\) on the left to \(6\) on the right; i.e., \(R\) “maps \(2\) to \(6\)” or \(R :2→ 6\).

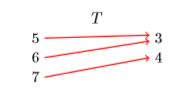
Example \(\PageIndex{3}\)

Create a mapping diagram for the relation in Example \(\PageIndex{1}\).

Solution

The relation of Example \(\PageIndex{1}\) is \(T=\{(5,3),(6,3),(7,4)\}\). List the domain \(\mathcal{D}=\{5,6,7\}\) on the left, the range \(\mathcal{R}=\{3,4\}\) on the right, then use arrows to indicate the ordered pairs (see Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\): A mapping diagram for the relation \(T\).

Function Definition

A function is a very special type of relation.

Function

A relation is a function if and only if each object in the domain is paired with exactly one object in the range.

As a first example, consider the relation \(R = \{(0,3),(0,4),(1,5),(2,6)\}\) whose mapping diagram is pictured in Figure \(\PageIndex{2}\). Note that \(0\) in the domain is paired with two objects, \(3\) and \(4\), in the range. Hence, relation \(R\) is is not a function.

As a second example, consider the relation \(T =\{(5,3),(6,3),(7,4)\}\), whose mapping diagram is pictured in Figure \(\PageIndex{3}\). In this example, each domain object is paired with exactly one range object: \(5\) only gets sent to \(3\), \(6\) only gets sent to \(3\), and \(7\) only gets sent to \(4\). Hence, the relation \(T\) is a function. The fact that the range object \(3\) is used twice does not matter. It’s the fact that each domain object gets sent to exactly one range object that matters.

Example \(\PageIndex{4}\)

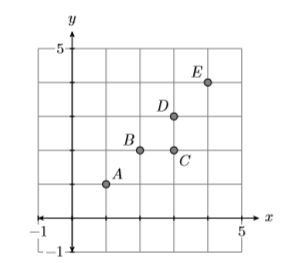
Consider the relation pictured in Figure \(\PageIndex{4}\). Is it a function?

Figure \(\PageIndex{4}\): Is this relation a function?

Solution

The graph in Figure \(\PageIndex{4}\) consists of the points \(A(1,1)\), \(B(2,2)\), \(C(3,2)\), \(D(3,3)\), and \(E(4,4)\). The domain is \(\mathcal{D}=\{1,2,3,4\}\) and the range is \(\mathcal{R}=\{1,2,3,4\}\). A mapping diagram (see Figure \(\PageIndex{5}\)) will help us decide if the relation represented by the graph is a function. Put the domain on the left, the range on the right, then use arrows to indicate the ordered pairs. Let’s call the relation \(f\).

Figure \(\PageIndex{5}\): A mapping diagram for the relation \(f\) depicted in Figure \(\PageIndex{4}\).

In Figure \(\PageIndex{5}\), note how the domain object \(3\) is “sent to” or paired with two range objects, \(2\) and \(3\). Hence, the relation \(f\) is not a function.

Exercise \(\PageIndex{4}\)

Consider the relation pictured below. Is it a function?

Answer

Yes, the relation is a function.

Example \(\PageIndex{5}\)

The following relation pairs automobiles with their gas mileage. Determine if the relation is a function.

\[T =\{\text {(Bentley Mulsanne,18),(Kia Soul,30),(Lamborghini Gallardo,20), (Smart Fortwo,41),(Jaguar XF,23)} \} \nonumber \]

Solution

In Figure \(\PageIndex{6}\), we create a mapping diagram indicating the relation between cars and their gas mileage. Note that each domain object on the left is paired with exactly one range object on the right. Hence, this relation is a function.

Figure \(\PageIndex{6}\): A mapping diagram for the relation \(T\).

Exercise \(\PageIndex{5}\)

The following relation pairs people with their age. Determine if the relation is a function.

\[S = \{\text {(Mary,23),(Joe,18), (Alfonzo,20),(Zoe,18), (Maria,22),(Chris,23) } \} \nonumber \]

Answer

Yes, the relation is a function.

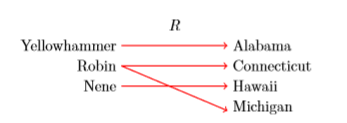
Example \(\PageIndex{6}\)

The following relation pairs a particular bird with the state that has adopted that bird as its state bird. Determine if the relation is a function.

\[R=\{\text { (Yellowhammer, Alabama), (Robin, Connecticut), (Nene, Hawaii), (Robin, Michigan) } \} \nonumber \]

Solution

In Figure \(\PageIndex{7}\), we create a mapping diagram indicating the relation between birds and their state adoptions. Note that the domain object “Robin” is paired with two range objects, “Connecticut” and “Michigan,” hence this relation is not a function.

Figure \(\PageIndex{7}\): A mapping diagram for the relation \(R\).

Exercise \(\PageIndex{6}\)

The following relation pairs people with the types of cars they own. Determine if the relation is a function.

\[S = \{\text {(Bernard,station wagon), (Tina,truck), (Gilberto,sedan), (Kate,sport utility), (Bernard,sedan), (Kate,minivan)} \} \nonumber \]

Answer

No, the relation is not a function.

Mapping Diagram Notation

The goal of this section is to introduce function notation. Let’s begin with the mapping diagram in Figure \(\PageIndex{8}\).

Figure \(\PageIndex{8}\): Mapping diagram.

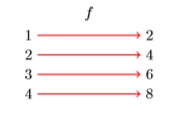
The mapping diagram in Figure \(\PageIndex{8}\) reveals the following facts:

• \(f\) maps \(1\) to \(2\) or \(f :1→ 2\)
• \(f\) maps \(2\) to \(4\) or \(f :2→ 4\)
• \(f\) maps \(3\) to \(6\) or \(f :3→ 6\)
• \(f\) maps \(4\) to \(8\) or \(f :4→ 8\)

Note how the notation \(f :4→ 8\) correlates nicely with the mapping diagram in Figure \(\PageIndex{8}\). The notation \(f :4→ 8\) is read “\(f\) maps \(4\) to \(8\)” or “ \(f\) sends \(4\) to \(8\).”

A closer look at the mapping diagram in Figure \(\PageIndex{8}\) reveals an interesting pattern. The “rule” seems to be that the relation \(f\) doubles each entry in its domain: twice \(1\) is \(2\), twice \(2\) is \(4\), twice \(3\) is \(6\), etc. It’s possible to give a general description of this “rule” by writing: \[f : x→ 2x (5.1) \label{Eq5.1.1} \]That is, \(f\) sends \(x\) to twice \(x\), or equivalently, \(2x\). For example, we might ask “where does \(f\) send \(15\)?” To answer this question, we would replace \(x\) with \(15\) in the rule \ref{Eq5.1.1} to get \[f : 15→ 2(15) \nonumber \]or equivalently, \[f : 15→ 30 \nonumber \]We could also ask “where does \(f\) send \(−7\)?” To answer this question, we would replace \(x\) with \(−7\) in the rule \ref{Eq5.1.1} to get \[f : −7→ 2(−7) \nonumber \]or equivalently, \[f : −7 →−14 \nonumber \]

Example \(\PageIndex{7}\)

Given the rule \(f : x → 2x + 3\), answer the question “where does \(f\) send \(8\)?”

Solution

To find where “\(f\) sends \(8\),” substitute \(8\) for \(x\) in the rule \(f : x → 2x + 3\) to get \[f :8→ 2(8) + 3 \nonumber \]or equivalently,\[f :8→ 19 \nonumber \]

Exercise \(\PageIndex{7}\)

Given the rule \(f : x → 3x−5\), answer the question “where does \(f\) send \(−2\)?”

Answer

\( f : −2 →−11\)

Example \(\PageIndex{8}\)

Given the rule \(f : x → x/(x+3)\), answer the question “where does \(f\) send \(−1\)?”

Solution

To find where “\(f\) sends \(−1\),” substitute \(−1\) for \(x\) in the rule \(f : x→ x/(x + 3)\) to get \[f :-1 \rightarrow \frac{-1}{-1+3} \nonumber \] or equivalently, \[f :-1 \rightarrow-\dfrac{1}{2} \nonumber \]

Exercise \(\PageIndex{8}\)

Given the rule \(f : x → 2x^2 +5x\), answer the question “where does \(f\) send \(3\)?”

Answer

\(f : 3 \rightarrow 33\)

In Examples \(\PageIndex{7}\) and \(\PageIndex{8}\), note that each time you substitute a value for \(x\) in the given rule, you get a unique answer. This means that each object in the domain of \(f\) is sent to a unique object in the range of \(f\), making the rules in Examples \(\PageIndex{7}\) and \(\PageIndex{8}\) functions. This leads us to an itemized description of a function.

Rule of Three

A function consists of three parts:

• a set of objects which mathematicians call the domain
• a second set of objects which mathematicians call the range
• a rule that describes how to assign each object in the domain to exactly one object in the range.

Function Notation

Although the mapping diagram notation \(f : x→ 3−4x\) is quite easy to understand, the standard function notation used is \(f(x)=3−4x\). With mapping diagram notation, if we want to answer the question “where does \(f\) send \(12\)?”, we write:

\[\begin{array}{c}{f : x \rightarrow 3-4 x} \\ {f : 12 \rightarrow 3-4(12)} \\ {f : 12 \rightarrow 3-48} \\ {f : 12 \rightarrow-45}\end{array} \nonumber \]

Hence, \(f : 12→−45\); i.e., \(f\) sends \(12\) to \(−45\). Function notation uses exactly the same concept; i.e, substitute \(12\) for \(x\).

Tips for Using Function Notation

1. Replace all occurrences of variables in the notation with open parentheses. Leave room between the parentheses to substitute the given value of the variable.
2. Substitute the given values of variables in the open parentheses prepared in the first step.
3. Evaluate the resulting expression according to the Rules Guiding Order of Operations.

Given \(f(x)=3−4x\), to evaluate \(f(12)\), first restate the function notation, then replace each occurrence of the variable with open parentheses.

\[\begin{aligned} f(x)&= 3-4 x \quad \color {Red} \text { Original function notation. } \\ f(\; \; ) &= 3-4(\; \; ) \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Now substitute \(12\) for \(x\) in the open parentheses prepared in the last step.

\[\begin{aligned} f({\color {Red} 12})&= 3-4({\color {Red} 12}) \quad \color {Red} \text { Substitute } 12 \text { for } x \text { in the open parentheses positions. } \\ f(12) &= 3-48 \quad \color {Red} \text { Multiply. } \\ f(12) &= -45 \quad \color {Red} \text { Subtract. } \end{aligned} \nonumber \]

Hence, \(f(12) =−45\); i.e., \(f\) sends \(12\) to \(−45\).

Example \(\PageIndex{9}\)

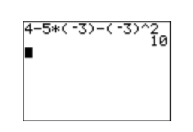
Given \(f(x)=4−5x−x^2\), evaluate \(f(−3)\).

Solution

Start by replacing each occurrence of the variable \(x\) with open parentheses.

\[\begin{aligned} f(x) &=4-5 x-x^{2} \quad \color {Red} \text { Original function notation. }\\ f( & )=4-5(\quad)-(\quad)^{2} \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Now substitute \(−3\) for \(x\) in the open parentheses prepared in the last step.

\[\begin{aligned} f({\color {Red}-3}) &= 4-5({\color {Red}-3})-({\color {Red}-3})^{2} \quad \color {Red} \text { Substitute }-3 \text { for } x \text { in the open parentheses positions. } \\ f(-3) &= 4-5(-3)-9 \quad \color {Red} \text { Evaluate exponent: }(-3)^{2}=9 \\ f(-3) &= 4+15-9 \quad \color {Red}\text { Multiply: }-5(-3)=15\\ f(-3) &= 10 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

Thus, \(f(−3) = 10\). Check this on your calculator (see Figure \(\PageIndex{9}\)).

Figure \(\PageIndex{9}\): Calculator check.

The next example demonstrates one of the advantages of function notation. For example, it is easy to refer to the function in which you want to substitute the given \(x\)-value.

Example \(\PageIndex{10}\)

Given \(f(x)=5−x\) and \(g(x)=x^2 −9\), find \(f(−1)\) and \(g(−2)\).

Solution

We’re given two function definitions, \(f\) and \(g\), but we’re first asked to find \(f(−1)\). This means that we must replace each occurrence of \(x\) with \(−1\) in the function \(f(x)=5−x\).

\[\begin{aligned} f(x) &= 5-x \quad \color {Red} \text { Original function notation. } \\ f(\;\;) &= 5-(\;\;) \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Now substitute \(−1\) for \(x\) in the open parentheses prepared in the last step.

\[\begin{aligned} f(-1) &= 5-(-1) \quad \color {Red} \text { Substitute }-1 \text { for } x \text { in the open } \\ &= 5+1 \quad \color {Red}\text { Add the opposite. } \\ &= 6 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

Thus, \(f(−1) = 6\). We’re next asked to find \(g(−2)\). This means that we must replace each occurrence of \(x\) with \(−2\) in the function \(g(x)=x^2 −9\).

\[\begin{aligned} g(x) &= x^{2}-9 \quad \color {Red} \text { Original function notation. } \\ g(\;\;) &= (\;\;)^{2}-9 \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Now substitute \(−2\) for \(x\) in the open parentheses prepared in the last step.

\[\begin{aligned} g({\color {Red}-2}) &= ({\color {Red}-2})^{2}-9 \quad \color {Red} \text { Substitute }-2 \text { for } x \text { in the open parentheses position. } \\ &= 4-9 \quad \color {Red} \text { Exponent first: }(-2)^{2}=4 \\ &= -5 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

Thus, \(g(−2) =−5\).

Exercise \(\PageIndex{10}\)

Given f\((x)=3x^2 −20\) and \(g(x)=4x +6/x\), find \(f(−3)\) and \(g(2)\).

Answer

\(f(−3) = 7\) and \(g(2) = 10\)

Interchanging \(y\) and \(f(x)\)

In most cases, \(y\) and \(f(x)\) are completely interchangeable. For example, compare and contrast the following two examples.

Question: Given \(y =3 x + 7\), find \(y\) when \(x\) equals \(5\).

Solution: Replace \(x\) with \(5\).

\[\begin{array}{l}{y=3 x+7} \\ {y=3(5)+7} \\ {y=15+7} \\ {y=22}\end{array} \nonumber \]

Question: Given \(f(x)=3 x + 7\), evaluate \(f(5)\)

Solution: Replace \(x\) with \(5\).

\[\begin{array}{l}{f(x)=3 x+7} \\ {f(5)=3(5)+7} \\ {f(5)=15+7} \\ {f(5)=22}\end{array} \nonumber \]

In each case, the answer is \(22\). However, in the first case, the answer \(y = 22\) disguises the fact that an \(x\)-value of \(5\) was used to arrive at the result. On the other hand, when we use function notation, the final answer \(f(5) = 22\) indicates that we used an \(x\)-value of \(5\) to determine that the \(y\)-value is \(22\). This is another advantage of function notation.

Let’s look at one final application demonstrating that \(y\) and \(f(x)\) are interchangeable.

Example \(\PageIndex{11}\)

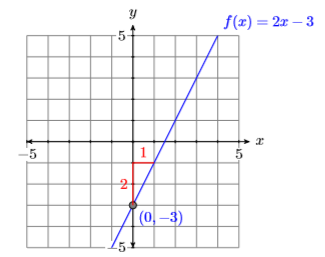
Sketch the graph of \(f(x)=2x−3\).

Solution

Because \(y\) and \(f(x)\) are interchangeable, the instruction is identical to “sketch the graph of \(y =2 x−3\).” The graph is a line, with slope \(2\) and \(y\) -intercept at \((0,−3)\). Plot the \(y\)-intercept at \((0,−3)\), then move up \(2\) and right \(1\) to create a line with slope \(2\) (see Figure \(\PageIndex{10}\)). Note how we’ve labeled the graph with its equation using function notation.

Figure \(\PageIndex{10}\): The graph of \(f(x)=2x−3\) is a line.

Exercise \(\PageIndex{11}\)

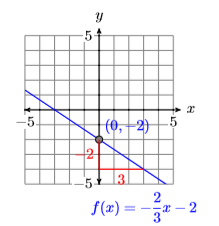
Sketch the graph of \(f(x)=-\dfrac{2}{3} x-2\)

Answer