5.4: Adding and Subtracting Polynomials

Last updated
Save as PDF

Page ID: 19880

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In this section we concentrate on adding and subtracting polynomial expressions, based on earlier work combining like terms in Ascending and Descending Powers. Let’s begin with an addition example.

Example $\PageIndex{1}$

Simplify: \[\left(a^{2}+3 a b-b^{2}\right)+\left(4 a^{2}+11 a b-9 b^{2}\right) \nonumber \]

Solution

Use the commutative and associative properties to change the order and regroup. Then combine like terms.

\[\begin{aligned}\left(a^{2}+3 a b-b^{2}\right) &+\left(4 a^{2}+11 a b-9 b^{2}\right) \\ &=\left(a^{2}+4 a^{2}\right)+(3 a b+11 a b)+\left(-b^{2}-9 b^{2}\right) \\ &=5 a^{2}+14 a b-10 b^{2} \end{aligned} \nonumber \]

Exercise $\PageIndex{1}$

Simplify: $\left(3 s^{2}-2 s t+4 t^{2}\right)+\left(s^{2}+7 s t-5 t^{2}\right)$

Answer: $4 s^{2}+5 s t-t^{2}$

Let’s combine some polynomial functions.

Example $\PageIndex{2}$

Given $f(x)=3x^2−4x−8$ and $g(x)=x^2−11x+15$, simplify $f(x)+g(x)$.

Solution

First, replace $f(x)$ and $g(x)$ with their deﬁnitions. Be sure to surround each polynomial with parentheses, because we are asked to add all of $f(x)$ to all of $g(x)$.

\[f(x)+g(x) = (3x^2 −4x−8) + (x^2 −11x + 15) \nonumber \] Now use the commutative and associative properties to change the order and regroup. Combine like terms.

\[\begin{array}{l}{=\left(3 x^{2}+x^{2}\right)+(-4 x-11 x)+(-8+15)} \\ {=4 x^{2}-15 x+7}\end{array} \nonumber \]

Hence, $f(x)+g(x)=4x^2 −15x + 7$.

Exercise $\PageIndex{2}$

Given $f(x)=2x^2 +9x−5$ and $g(x)=−x^2 −4x + 3$, simplify $f(x)+g(x)$.

Answer: $x^{2}+5 x-2$

If you are comfortable skipping a step or two, it is not necessary to write down all of the steps shown in Examples $\PageIndex{1}$ and $\PageIndex{2}$. Let’s try combining like terms mentally in the next example.

Example $\PageIndex{3}$

Simplify: \[\left(x^{3}-2 x^{2} y+3 x y^{2}+y^{3}\right)+\left(2 x^{3}-4 x^{2} y-8 x y^{2}+5 y^{3}\right) \nonumber \]

Solution

If we use the associative and commutative property to reorder and regroup, then combine like terms, we get the following result.

\[\begin{aligned}\left(x^{3}-2 x^{2} y\right.&+3 x y^{2}+y^{3} )+\left(2 x^{3}-4 x^{2} y-8 x y^{2}+5 y^{3}\right) \\ &=\left(x^{3}+2 x^{3}\right)+\left(-2 x^{2} y-4 x^{2} y\right)+\left(3 x y^{2}-8 x y^{2}\right)+\left(y^{3}+5 y^{3}\right) \\ &=3 x^{3}-6 x^{2} y-5 x y^{2}+6 y^{3} \end{aligned} \nonumber \]

However, if we can combine like terms mentally, eliminating the middle step, it is much more eﬃcient to write:

\[\begin{array}{l}{\left(x^{3}-2 x^{2} y+3 x y^{2}+y^{3}\right)+\left(2 x^{3}-4 x^{2} y-8 x y^{2}+5 y^{3}\right)} \\ {\quad \quad=3 x^{3}-6 x^{2} y-5 x y^{2}+6 y^{3}}\end{array} \nonumber \]

Exercise $\PageIndex{3}$

Simplify: $\left(-5 a^{2} b+4 a b-3 a b^{2}\right)+\left(2 a^{2} b+7 a b-a b^{2}\right)$

Answer: $-3 a^{2} b+11 a b-4 a b^{2} d$

Negating a Polynomial

Before attempting subtraction of polynomials, let’s ﬁrst address how to negate or “take the opposite” of a polynomial. First recall that negating is equivalent to multiplying by $−1$.

Negating

If $a$ is any number, then

\[−a =(−1)a. \nonumber \]

That is, negating is equivalent to multiplying by $−1$.

We can use this property to simplify $−(a + b)$. First, negating is identical to multiplying by $−1$. Then we can distribute the $−1$.

\[\begin{aligned} -(a+b) &= (-1)(a+b) \quad \color {Red} \text { Negating is equivalent to multiplying by } -1 \\ &= (-1) a+(-1) b \quad \color {Red} \text { Distribute the }-1 . \\ &= -a+(-b) \quad \color {Red} \text { Simplify: }(-1) a=-a \text { and }(-1) b=-b \\ &= -a-b \quad \color {Red} \text { Subtraction means add the opposite. } \end{aligned} \nonumber \]

Thus, $−(a + b)=−a −b$. However, it is probably simpler to note that the minus sign in front of the parentheses simply changed the sign of each term inside the parentheses.

Negating a sum

When negating a sum of terms, the eﬀect of the minus sign is to change each term in the parentheses to the opposite sign. \[−(a + b)=−a−b \nonumber \]

Let’s look at this principle in the next example.

Example $\PageIndex{4}$

Simplify: $-\left(-3 x^{2}+4 x-8\right)$

Solution

First, negating is equivalent to multiplying by $−1$. Then distribute the $−1$.

\[\begin{aligned} -&\left(-3 x^{2}+4 x-8\right) \\ &=(-1)\left(-3 x^{2}+4 x-8\right) \quad \color {Red} \text{Negating is equivalent to multiplying by } -1\\ &=(-1)\left(-3 x^{2}\right)+(-1)(4 x)-(-1)(8) \quad \color {Red} \text {Distribute the } -1 \\ &=3 x^{2}+(-4 x)-(-8) \quad \color {Red} \text {Simplify: } (-1)(-3 x^{2})=3 x^{2}, (-1)(4 x)=-4 x, \text {and} (-1)(8)=-8\\ &=3 x^{2}-4 x+8 \quad \color {Red} \text {Subtraction means add the opposite.} \end{aligned} \nonumber \]

Alternate solution:

As we saw above, a negative sign in front of a parentheses simply changes the sign of each term inside the parentheses. So it is much more eﬃcient to write\[−(−3x^2 +4x−8) = 3x^2 −4x +8 \nonumber \]simply changing the sign of each term inside the parentheses.

Exercise $\PageIndex{4}$

Simplify: $-\left(2 x^{2}-3 x+9\right)$

Answer: $-2 x^{2}+3 x-9$

Subtracting Polynomials

Now that we know how to negate a polynomial (change the sign of each term of the polynomial), we’re ready to subtract polynomials.

Example $\PageIndex{5}$

Simplify: $\left(y^{3}-3 y^{2} z+4 y z^{2}+z^{3}\right)-\left(2 y^{3}-8 y^{2} z+2 y z^{2}-8 z^{3}\right)$

Solution

First, distribute the minus sign, changing the sign of each term of the second polynomial.

\[\left(y^{3}-3 y^{2} z+4 y z^{2}+z^{3}\right)-\left(2 y^{3}-8 y^{2} z+2 y z^{2}-8 z^{3}\right)=y^{3}-3 y^{2} z+4 y z^{2}+z^{3}-2 y^{3}+8 y^{2} z-2 y z^{2}+8 z^{3} \nonumber \]

Regroup, combining like terms. You may perform this next step mentally if you wish.

\[\begin{array}{l}{=\left(y^{3}-2 y^{3}\right)+\left(-3 y^{2} z+8 y^{2} z\right)+\left(4 y z^{2}-2 y z^{2}\right)+\left(z^{3}+8 z^{3}\right)} \\ {=-y^{3}+5 y^{2} z+2 y z^{2}+9 z^{3}}\end{array} \nonumber \]

Exercise $\PageIndex{5}$

Simplify: $\left(4 a^{2} b+2 a b-7 a b^{2}\right)-\left(2 a^{2} b-a b-5 a b^{2}\right)$

Answer: $2 a^{2} b+3 a b-2 a b^{2}$

Let’s subtract two polynomial functions.

Example $\PageIndex{6}$

Given $p(x)=−5x^3 +6 x − 9$ and $q(x)=6 x^2 − 7x − 11$, simplify $p(x)−q(x)$.

Solution

First, replace $p(x)$ and $q(x)$ with their deﬁnitions. Because we are asked to subtract all of $q(x)$ from all of $p(x)$, it is critical to surround each polynomial with parentheses.

\[p(x)-q(x)=\left(-5 x^{3}+6 x-9\right)-\left(6 x^{2}-7 x-11\right) \nonumber \]

Distribute the minus sign, changing the sign of each term in the second polynomial, then regroup and combine like terms.

\[\begin{array}{l}{=-5 x^{3}+6 x-9-6 x^{2}+7 x+11} \\ {\color {Red} =-5 x^{3}-6 x^{2}+(6 x+7 x)+(-9+11)} \\ {=-5 x^{3}-6 x^{2}+13 x+2}\end{array} \nonumber \]

However, after distributing the minus sign, if we can combine like terms mentally, eliminating the middle step, it is much more eﬃcient to write:

\[\begin{aligned} p(x)-q(x) &=\left(-5 x^{3}+6 x-9\right)-\left(6 x^{2}-7 x-11\right) \\ &=-5 x^{3}+6 x-9-6 x^{2}+7 x+11 \\ &=-5 x^{3}-6 x^{2}+13 x+2 \end{aligned} \nonumber \]

Exercise $\PageIndex{6}$

Given $f(x)=3x^2 +9x−4$ and $g(x)=−5x2 +4x−6$, simplify $f(x)−g(x)$.

Answer: $8 x^{2}+5 x+2$

Some Applications

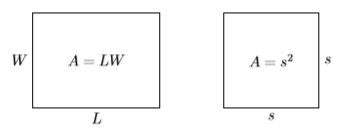
Recall that the area of a rectangle having length $L$ and width $W$ is found using the formula $A = LW$. The area of a square having side s is found using the formula $A = s^2$ (see Figure $\PageIndex{1}$).

fig 5.4.1.png — Figure $\PageIndex{1}$: Area formulae for the rectangle and square.

Example $\PageIndex{7}$

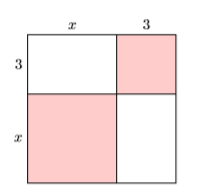
Find the area of the square in Figure $\PageIndex{2}$ by summing the area of its parts.

fig 5.4.2.png — Figure $\PageIndex{2}$: Find the sum of the parts.

Solution

Let’s separate each of the four pieces and label each with its area (see Figure $\PageIndex{3}$).

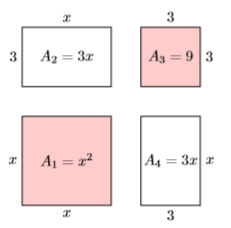
fig 5.4.3.png — Figure $\PageIndex{3}$: Finding the area of each of the four parts.

The two shaded squares in Figure $\PageIndex{3}$ have areas $A_1 = x^2$ and $A_3 = 9$, respectively. The two unshaded rectangles in Figure $\PageIndex{3}$ have areas $A_2 =3 x$ and $A_4 =3x$. Summing these four areas gives us the area of the entire ﬁgure.

\[\begin{aligned} A &=A_{1}+A_{2}+A_{3}+A_{4} \\ &=x^{2}+3 x+9+3 x \\ &=x^{2}+6 x+9 \end{aligned} \nonumber \]

Exercise $\PageIndex{7}$

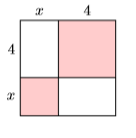
Find the area of the square shown below by summing the area of its parts.

Answer: $x^{2}+8 x+16$

Example $\PageIndex{8}$

Ginger runs a business selling wicker baskets. Her business costs for producing and selling $x$ wicker baskets are given by the polynomial function $C(x)=100+3x−0.02x^2$. The revenue she earns from selling $x$ wicker baskets is given by the polynomial function $R(x)=2.75x$. Find a formula for $P(x)$, the proﬁt made from selling $x$ wicker baskets. Use your formula to determine Ginger’s proﬁt if she sells $123$ wicker baskets.

Solution

The proﬁt made from selling $x$ wicker baskets is found by subtracting the costs incurred from the revenue received. In symbols: \[P(x)=R(x)−C(x) \nonumber \]
Next, replace $R(x)$ and $C(x)$ with their deﬁnitions. Because we are supposed to subtract all of the cost from the revenue, be sure to surround the cost polynomial with parentheses.\[P(x)=2 .75x−(100 + 3x−0.02x^2) \nonumber \]
Distribute the minus sign and combine like terms.

\[\begin{array}{l}{=2.75 x-100-3 x+0.02 x^{2}} \\ {=0.02 x^{2}-0.25 x-100}\end{array} \nonumber \]

Thus, the proﬁt function is $P(x)=0 .02x^2 −0.25x−100$.

Next, to determine the proﬁt if $123$ wicker baskets are sold, substitute $123$ for $x$ in the proﬁt function $P(x)$.

\[\begin{aligned} P(x) &=0.02 x^{2}-0.25 x-100 \\ P(123) &=0.02(123)^{2}-0.25(123)-100 \end{aligned} \nonumber \]

You can now use your graphing calculator to determine the proﬁt (see Figure $\PageIndex{5}$). Hence, the proﬁt made from selling $123$ wicker baskets is $\$171.83$.

fig 5.4.5.png — Figure $\PageIndex{5}$: Determining the proﬁt from selling $123$ wicker baskets.

Exercise $\PageIndex{8}$

The costs for producing and selling $x$ widgets are given by the polynomial function $C(x) = 50 + 5x−0.5x^2$, and the revenue for selling $x$ widgets is given by the polynomial function $R(x)=3.5x$. Determine the proﬁt if $75$ widgets are sold.

Answer: $\$ 2,650$

Search

Text Color

Text Size

Margin Size

Font Type