2.9: Exercise Supplement
- Page ID
- 49353
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise Supplement
Symbols and Notations
For the following problems, simplify the expressions.
\(12 + 7(4 + 3)\)
- Answer
-
\(61\)
\(9(4 - 2) + 6(8 + 2) - 3(1 + 4)\)
\(6[1 + 8(7 + 2)]\)
- Answer
-
\(438\)
\(26 \div 2 - 10\)
\(\dfrac{(4+17+1)+4}{14-1}\)
- Answer
-
\(2\)
\(51 \div 3 \div 7\)
\((4 + 5)(4 + 6) - (4 + 7)\)
- Answer
-
\(79\)
\(8(2 \cdot 12 \div 13) + 2 \cdot 5 \cdot 11 - [1 + 4(1 + 2)]\)
\(\dfrac{3}{4} + \dfrac{1}{12}(\dfrac{3}{4} - \dfrac{1}{2})\)
- Answer
-
\(\dfrac{37}{47}\)
\(48 - 3[\dfrac{1 + 17}{6}]\)
\(\dfrac{29 + 11}{6 - 1}\)
- Answer
-
\(8\)
\(\dfrac{\dfrac{88}{11} + \dfrac{99}{9} + 1}{\dfrac{54}{9} - \dfrac{22}{11}}\)
\(\dfrac{8 \cdot 6}{2} + \dfrac{9 \cdot 9}{3} \dfrac{10 \cdot 4}{5}\)
- Answer
-
\(43\)
For the following problems, write the appropriate relation symbol (=,<,>) in place of the ∗.
\(22 * 6\)
\(9[4 + 3(8)] * 6[1 + 8(5)]\)
- Answer
-
\(252 > 246\)
\(3(1.06 + 2.11) * 4(11.01 - 9.06)\)
\(2 * 0\)
- Answer
-
\(2 > 0\)
For the following problems, state whether the letters or symbols are the same or different.
\(<\) and \(\not \ge\)
\(>\) and \(\not <\)
- Answer
-
Different
\(a = b\) and \(b = a\)
Represent the sum of \(c\) and \(d\) two different ways.
- Answer
-
\(c + d\) ; \(d + c\)
For the following problems, use algebraic notataion.
\(8\) plus \(9\)
\(62\) divided by \(f\)
- Answer
-
\(\dfrac{62}{f}\) or \(62 \div f\)
\(8\) times \((x + 4)\)
\(6\) times \(x\), minus \(2\)
- Answer
-
\(6x - 2\)
\(x + 1\) divided by \(x - 3\)
\(y + 11\) divided by \(y + 10\), minus \(12\)
- Answer
-
\((y + 11) \div (y + 10) - 12\) or \(\dfrac{y + 11}{y + 10} - 12\)
zero minus \(a\) times \(b\)
The Real Number Line and the Real Numbers
Is every natural number a whole number?
- Answer
-
Yes
Is every rational number a real number?
For the following problems, locate the numbers on a number line by placing a point at their (approximate) position.
\(2\)
- Answer
-
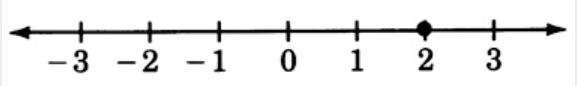
\(3.6\)
\(-1\dfrac{3}{8}\)
- Answer
-

\(0\)
\(-4\dfrac{1}{2}\)
- Answer
-

Draw a number line that extends from 10 to 20. Place a point at all odd integers.
Draw a number line that extends from \(−10\) to \(10\). Place a point at all negative odd integers and at all even positive integers.
- Answer
-

Draw a number line that extends from \(−5\) to \(10\). Place a point at all integers that are greater then or equal to \(−2\) but strictly less than \(5\).
Draw a number line that extends from \(−10\) to \(10\). Place a point at all real numbers that are strictly greater than \(−8\) but less than or equal to \(7\).
- Answer
-

Draw a number line that extends from \(−10\) to \(10\). Place a point at all real numbers between and including \(−6\) and \(4\).
For the following problems, write the appropriate relation symbol (=,<,>).
\(-3\) \(0\)
- Answer
-
\(-3 < 0\)
\(-1\) \(1\)
\(-8\) \(-5\)
- Answer
-
\(-8 < -5\)
\(-5\) \(-5\dfrac{1}{2}\)
Is there a smallest two digit integer? If so, what is it?
- Answer
-
Yes, \(-99\)
Is there a smallest two digit real number? If so, what is it?
For the following problems, what integers can replace x so that the statements are true?
\(4 \le x \le 7\)
- Answer
-
\(4, 5, 6\) or \(7\)
\(-3 \le x < 1\)
\(-3\) \(0\)
- Answer
-
\(-3 < 0\)
\(-3 < x \le 2\)
- Answer
-
\(-2, -1, 0, 1\), or \(2\)
The temperature today in Los Angeles was eighty-two degrees. Represent this temperature by real number.
The temperature today in Marbelhead was six degrees below zero. Represent this temperature by real number.
- Answer
-
\(-6°\)
On the number line, how many units between \(-3\) and \(2\)?
- Answer
-
\(-3 < 0\)
On the number line, how many units between \(-4\) and \(0\)?
- Answer
-
\(4\)
Properties of the Real Numbers
\(a + b = b + a\) is an ilustration of the property of addition.
\(st = ts\) is an illustration of the _________ property of __________.
- Answer
-
commutative, multiplication
Use the commutative properties of addition and multiplication to write equivalent expressions for the following problems.
\(y + 12\)
\(a + 4b\)
- Answer
-
\(4b + a\)
\(6x\)
\(2(a-1)\)
- Answer
-
\((a-1)2\)
\((-8)(4)\)
\((6)(-9)(-2)\)
- Answer
-
\((-9)(6)(-2)\) or \((-9)(-2)(6)\) or \((6)(-2)(-9)\) or \((-2)(-9)(6)\)
\((x + y)(x - y)\)
\(△ \cdot ⋄\)
- Answer
-
\( ⋄\cdot △\)
Simplify the following problems using the commutative property of multiplication. You need not use the distributive property.
\(8x3y\)
\(16ab2c\)
- Answer
-
\(32abc\)
\(4axyc4d4e\)
\(3(x+2)5(x−1)0(x+6)\)
- Answer
-
\(0\)
\(8b(a−6)9a(a−4)\)
For the following problems, use the distributive property to expand the expressions.
\(3(a + 4)\)
- Answer
-
\(3a + 12\)
\(a(b + 3c)\)
\(2g(4h + 2k\)
- Answer
-
\(8gh+4gk\)
\((8m+5n)6p\)
\(3y(2x+4z+5w)\)
- Answer
-
\(6xy+12yz+15wy\)
\((a+2)(b+2c)\)
\((x+y)(4a+3b)\)
- Answer
-
\(4ax+3bx+4ay+3by\)
\(10a_z(b_z + c)\)
Exponents
For the following problems, write the expressions using exponential notation.
\(x\) to the fifth.
- Answer
-
\(x^5\)
\(y + 2\) cubed.
\((a+2b)\) squared minus \((a+3b)\) to the fourth.
- Answer
-
\((a + 2b)^2 - (a + 3b)^4\)
\(x\) cubed plus \(2\) times \((y−x)\) to the seventh.
\(aaaaaaa\)
- Answer
-
\(a^7\)
\(2 \cdot 2 \cdot 2 \cdot 2\)
\((−8)(−8)(−8)(−8)xxxyyyyy\)
- Answer
-
\((-8)^4x^3y^5\)
\((x-9)(x-9) + (3x + 1)(3x + 1)(3x + 1)\)
\(2zzyzyyy + 7zzyz(a - 6)^2(a-6)\)
- Answer
-
\(2y^4z^3 + 7yz^3(a-6)^3\)
For the following problems, expand the terms so that no exponents appear.
\(x^3\)
\(3x^3\)
- Answer
-
\(3xxx\)
\(7^3x^2\)
\((4b)^2\)
- Answer
-
\(4b \cdot 4b\)
\((6a^2)^3(5c-4)^2\)
\((x^3+7)^2(y^2-3)^3(z+10)\)
- Answer
-
\((xxx+7)(xxx+7)(yy−3)(yy−3)(yy−3)(z+10)\)
Choose values for \(a\) and \(b\) to show that:
a. \(a+b)^2\) is not always equal to \(a^2 + b^2\)
b. \((a+b)^2\) may be equal to \(a^2 + b^2\)
Choose value for \(x\) to show that
a. \((4x)^2\) is not always equal to \(4x^2\).
b. \((4x)^2\) may be equal to \(4x^2\)
- Answer
-
(a) any value except zero
(b) only zero
Rules of Exponents - The Power Rules for Exponents
Simplify the following problems.
\(4^2 + 8\)
\(6^3 + 5(30)\)
- Answer
-
\(366\)
\(1^8 + 0^{10} + 3^2(4^2 + 2^3)\)
\(12^2 + 0.3(11)^2\)
- Answer
-
\(180.3\)
\(\dfrac{3^4 + 1}{2^2 + 4^2 + 3^2}\)
\(\dfrac{6^2 + 3^2}{2^2 + 1} + \dfrac{(1+4)^2 - 2^3 - 1^4}{2^5-4^2}\)
- Answer
-
\(10\)
\(a^4a^3\)
\(2b^52b^3\)
- Answer
-
\(4b^8\)
\(4a^3b^2c^8 \cdot 3ab^2c^0\)
\((6x^4y^{10})(xy^3)\)
- Answer
-
\(6x^5y^{13}\)
\((3xyz^2)(2x^2y^3)(4x^2y^2z^4)\)
\((3a)^4\)
- Answer
-
\(81a^4\)
\((10xy)^2\)
\((x^2y^4)^6\)
- Answer
-
\(x^{12}y^{24}\)
\((a^4b^7c^7z^{12})^9\)
\((\dfrac{3}{4}x^8y^6z^0a^{10}b^{15})^2\)
- Answer
-
\(\dfrac{9}{16}x^{16}y^{12}a^{20}b^{30}\)
\(\dfrac{14a^4b^6c^7}{2ab^3c^2}\)
- Answer
-
\(7a^3b^3c^5\)
\(\dfrac{11x^4}{11x^4}\)
\(x^4 \cdot \dfrac{x^{10}}{x^3}\)
- Answer
-
\(x^{11}\)
\(a^3b^7 \cdot \dfrac{a^9b^6}{a^5b^{10}}\)
\(\dfrac{(x^4y^6z^{10})^4}{(xy^5z^7)^3}\)
- Answer
-
\(x^{13}y^9z^{19}\)
\(\dfrac{(2x-1)^{13}(2x+5)^5}{(2x-1)^{10}(2x+5)}\)
\((\dfrac{3x^2}{4y^3})^2\)
- Answer
-
\(\dfrac{9x^4}{16y^6}\)
\(\dfrac{(x+y)^9(x-y)^4}{(x+y)^3}\)
\(x^n \cdot x^m\)
- Answer
-
\(x^{n+m}\)
\(a^{n+2}a^{n+4}\)
\(6b^{2n+7} \cdot 8b^{5n+2}\)
- Answer
-
\(48b^{7n+9}\)
\(\dfrac{18x^{4n+9}}{2x^{2n+1}}\)
\((x^{5t}y^{4r})^7\)
- Answer
-
\(x^{35t}y^{28r}\)
\((a^{2n}b^{3m}c^{4p})^{6r}\)
\(\dfrac{u^w}{u^k}\)
- Answer
-
\(u^{w-k}\)


