5.4: Further Techniques in Problem Solving
- Page ID
- 49369
Combining Techniques in Equation Solving
In Sections 5.2 and 5.3 we worked with techniques that involved the use of addition, subtraction, multiplication, and division to solve equations. We can combine these techniques to solve more complicated equations. To do so, it is helpful to recall that an equation is solved for a particular variable when all other numbers and/or letters have been disassociated from it and it is alone on one side of the equal sign. We will also note that
To associate numbers and letters we use the order of operations.
- Multiply/divide
- Add/subtract
To undo an association between numbers and letters we use the order of operations in reverse.
- Add/subtract
- Multiply/divide
Sample Set A
Solve \(4x - 7 = 9\) for \(x\).
\(\begin{array}{flushleft}
4x-7&=&9&\text{First, undo the association between } x \text{ and } 7.\\
&&&\text{The } 7 \text{ is associated with } x \text{ by subtraction.}\\
&&&\text{Undo the association by adding } 7 \text{ to both sides.}\\
4x-7+7&=&9+7\\
4x&=&16&\text{Now, undo the association between } x { and } 4.\\
&&&\text{The } 4 \text{ is associated with } x \text{ by multiplication.}\\
&&&\text{Undo the association by dividing both sides by } 4.\\
\dfrac{4x}{4}&=&\dfrac{16}{4}\\
16-7&=&9&\text{Is this correct? }\\
x&=&4
\end{array}\)
Check:
\(\begin{array}{flushleft}
4(4)-7&=&9&\text{Is this correct?}\\
9&=&9&\text{Yes, this is correct}.
\end{array}\)
Solve \(\dfrac{3y}{4}-5=-11\).
\(\begin{array}{flushleft}
\dfrac{3y}{4}-5&=&-11&-5\text{ is associated with } y \text{ by subtraction.}\\
&&&\text{Undo the association by adding } 5 \text{ to both sides}\\
\dfrac{3y}{4}-5+5&=&-11+5\\
\dfrac{3y}{4}&=&-6&4\text{ is associated with } y \text{ by division}.\\
&&&\text{Undo the association by multiplying both sides by } 4.\\
4 \cdot \dfrac{3y}{4}&=&4(-6)\\
3y&=&-24&3\text{ is associated with } y \text{ by multiplication.}\\
&&&\text{ Undo the association by dividing both sides by } 3.\\
\dfrac{3y}{3}&=&\dfrac{-24}{3}\\
\dfrac{3y}{3}&=&-8\\
y&=&-8
\end{array}\)
Check:
\(\begin{array}{flushleft}
\dfrac{3(-8)}{4}-5&=&-11&\text{Is this correct?}\\
\dfrac{-24}{4}-5&=&-11&\text{Is this correct?}\\
-6-5&=&-11&\text{Is this correct?}\\
-11&=&-11&\text{Yes, this is correct}
\end{array}\)
Solve \(\dfrac{8a}{3b} + 2m = 6m - 5\) for \(a\).
\(\begin{array}{flushleft}
\dfrac{8a}{3b}+2m&=&6m-5&2m\text{ is associated with } a \text{ by addition. Undo the association}\\
&&&\text{by subtracting } 2m \text{ from both sides.}\\
\dfrac{8a}{3b}+2m-2m&=&6m-5-2m\\
\dfrac{8a}{3b}&=&4m-5&3b\text{associated with } a \text{ by division. Undo the association}\\
&&&\text{by multiplying both sides by } 3b.\\
(3b)(\dfrac{8a}{3b})&=&3b(4m-5)\\
8a&=&12bm-15b&8\text{ is associated with } a \text{ by multiplication. Undo the}\\
&&&\text{multiplication by dividing both sides by } 8.\\
\dfrac{8a}{8}&=&\dfrac{12bm-15b}{8}\\
a&=&\dfrac{12bm-15b}{8}
\end{array}\)
Practice Set A
Solve \(3y−1=11\) for \(y\).
- Answer
-
\(y = 4\)
Solve \(\dfrac{5m}{2} + 6 = 1\) for \(m\).
- Answer
-
\(m=−2\)
Solve \(2n+3m=4\) for \(n\).
- Answer
-
\(n = \dfrac{4-3m}{2}\)
Solve \(\dfrac{9k}{2h}+5=p-2\) for \(k\)
- Answer
-
\(k = \dfrac{2hp-14h}{9}\)
Sometimes when solving an equation it is necessary to simplify the expressions composing it.
Sample Set B
Solve \(4x+1-3x = (-2)(4)\) for \(x\).
\(\begin{array}{flushleft}
4x+1-3x&=&(-2)(4)\\
x+1&=&-8\\
x&=&-9\\
\end{array}\)
Check:
\(\begin{array}{flushleft}
4(-9)+1-3(-9)&=&-8&\text{Is this correct?}\\
-36+1+27&=&-8&\text{Is this correct?}\\
-8&=&-8&\text{Yes, this is correct.}
\end{array}\)
Solve \(3(m-6)-2m=-4+1\) for \(m\).
\(\begin{array}{flushleft}
3(m-6)-2m&=&-4+1\\
3m-18-2m&=&-3\\
m-18&=&-3\\
m&=&15
\end{array}\)
Check:
\(\begin{array}{flushleft}
3(15-6)-2(15)&=&-4+1&\text{Is this correct?}\\
3(9)-30&=&-3&\text{Is this correct?}\\
27-30&=&-3&\text{Is this correct?}\\
-3&=&-3&\text{Yes, this is correct}
\end{array}\)
Practice Set B
Solve and check each equation.
\(16x−3−15x=8\) for \(x\).
- Answer
-
\(x=11\)
\(4(y−5)−3y=−1\) for \(y\).
- Answer
-
\(y=19\)
\(-2(a^2+3a-1)+2a^2+7a=0\) for \(a\).
- Answer
-
\(a=−2\)
\(5m(m-2a-1)-5m^2+2a(5m+3)=10\) for \(a\).
- Answer
-
\(a = \dfrac{10+5m}{6}\)
Often the variable we wish to solve for will appear on both sides of the equal sign. We can isolate the variable on either the left or right side of the equation by using the techniques of Sections 5.2 and 5.3.
Sample Set C
Solve \(6x-4=2x+8\) for \(x\).
\(\begin{array}{flushleft}
6x-4&=&2x+8&\text{To isolate } x \text{ on the left side, subtract } 2x \text{ from both sides.}\\
6x-4-2x&=&2x+8-2x\\
4x-4&=&8&\text{Add } 4 \text{ to both sides.}\\
4x-4+4&=&8+4\\
4x&=&12&\text{Divide both sides by } 4\\
\dfrac{4x}{4}&=&\dfrac{12}{4}\\
x&=&3
\end{array}\)
Check:
\(\begin{array}{flushleft}
6(3)-4&=&2(3)+8&\text{Is this correct?}\\
18-4&=&6+8&\text{Is this correct?}\\
14&=&14&\text{Yes, this is correct.}
\end{array}\)
Solve \(6(1-3x)+1=2x-[3(x-7)-20]\) for \(x\).
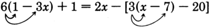
\(\begin{array}{flushleft}
6-18x+1&=&2x-[3x-21-20]\\
-18x+7&=&2x-[3x-41]\\
-18x+7&=&2x-3x+41\\
-18x+7&=&-x+41&\text{To isolate } x \text{ on the right side, add } 18x \text{ to both sides.}\\
-18x+7+18x&=&-x+41+18x\\
7&=&17x+41&\text{Subtract } 41 \text{ from both sides}.\\
7-41&=&17x+41-41\\
-34&=&17x&\text{Divide both sides by } 17.\\
\dfrac{-34}{17}&=&\dfrac{17x}{17}\\
-2&=&x&\text{Since the equation} -2=x \text{ is equivalent to the equation }\\
&&&x=-2, \text{ we can write the answer as } x=-2.\\
x&=&-2
\end{array}\)
Check:
\(\begin{array}{flushleft}
6(1-(3(-2))+1&=&2(-2)-[3(-2-7)-20]&\text{Is this correct?}\\
6(1+6)+1&=&−4−[3(−9)−20]&\text{Is this correct?}\\
6(7)+1&=&-4-[-27-20]&\text{Is this correct?}\\
42+1&=&-4-[-47]&\text{Is this correct?}\\
43&=&-4+47&\text{Is this correct?}\\
43&=&43&\text{Yes, this is correct}\\
\end{array}\)
Practice Set C
Solve \(8a+5=3a−5\) for \(a\).
- Answer
-
\(a=−2\)
Solve \(9y+3(y+6)=15y+21\) for \(y\).
- Answer
-
\(y=−1\)
Solve \(3k+2[4(k−1)+3]=63−2k\) for \(k\).
- Answer
-
\(k=5\)
Recognizing Identities and Contradictions
As we noted in Section 5.2, some equations are identities and some are contradictions. As the problems of Sample Set D will suggest,
Recognizing an Identity
- If, when solving an equation, all the variables are eliminated and a true statement results, the equation is an identity.
Recognizing a Contradiction
- If, when solving an equation, all the variables are eliminated and a false statement results, the equation is a contradiction.
Sample Set D
Solve \(9x + 3(4-3x) = 12\) for \(x\)
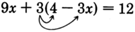
\(\begin{array}{flushleft}
9x+12-9x&=&12\\
12&=&12
\end{array}\)
The variable has been eliminated and the result is a true statement. The original equation is an identity.
Solve \(-2(10-2y)-4y+1=-18\) for \(y\)
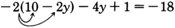
\(\begin{array}{flushleft}
-20+4y-4y+1&=&-18\\
-19&=&-18
\end{array}\)
The variable has been eliminated and the result is a false statement. The original equation is a contradiction.
Practice Set D
Classify each equation as an identity or a contradiction.
\(6x+3(1−2x)=3\)
- Answer
-
identity, \(3=3\)
\(−8m+4(2m−7)=28\)
- Answer
-
contradiction, \(−28=28\)
\(3(2x−4)−2(3x+1)+14=0\)
- Answer
-
identity, \(0=0\)
\(−5(x+6)+8=3[4−(x+2)]−2x\)
- Answer
-
contradiction, \(−22=6\)
Exercises
For the following problems, solve each conditional equation. If the equation is not conditional, identify it as an identity or a contradiction.
\(3x+1=16\)
- Answer
-
\(x=5\)
\(6y−4=20\)
\(4a−1=27\)
- Answer
-
\(a=7\)
\(3x+4=40\)
\(2y+7=−3\)
- Answer
-
\(y=−5\)
\(8k−7=−23\)
\(5x+6=−9\)
- Answer
-
\(x=−3\)
\(7a+2=−26\)
\(10y−3=−23\)
- Answer
-
\(y=−2\)
\(14x+1=−55\)
\(\dfrac{x}{9} + 2 = 6\)
- Answer
-
\(x=36\)
\(\dfrac{m}{7} - 8 = -11\)
\(\dfrac{y}{4}+6=12\)
- Answer
-
\(y=24\)
\(\dfrac{x}{8}-2=5\)
\(\dfrac{m}{11}-15=-19\)
- Answer
-
\(m=−44\)
\(\dfrac{k}{15}+20=10\)
\(6+\dfrac{k}{5}=5\)
- Answer
-
\(k=−5\)
\(1-\dfrac{n}{2}=6\)
\(\dfrac{7x}{4}+6=-8\)
- Answer
-
\(x=−8\)
\(\dfrac{-6m}{5}+11=-13\)
\(\dfrac{3k}{14} + 25 = 22\)
- Answer
-
\(k=-14\)
\(3(x−6)+5=−25\)
\(16(y−1)+11=−85\)
- Answer
-
\(y=−5\)
\(6x+14=5x−12\)
\(23y−19=22y+1\)
- Answer
-
\(y=20\)
\(−3m+1=3m−5\)
\(8k+7=2k+1\)
- Answer
-
\(k=−1\)
\(12n+5=5n−16\)
\(2(x−7)=2x+5\)
- Answer
-
contradiction
\(−4(5y+3)+5(1+4y)=0\)
\(3x+7=−3−(x+2)\)
- Answer
-
\(x=−3\)
\(4(4y+2)=3y+2[1−3(1−2y)]\)
\(5(3x−8)+11=2−2x+3(x−4)\)
- Answer
-
\(x = \dfrac{19}{14}\)
\(12−(m−2)=2m+3m−2m+3(5−3m)\)
\(−4 \cdot k−(−4−3k)=−3k−2k−(3−6k)+1\)
- Answer
-
\(k = 3\)
\(3[4−2(y+2)]=2y−4[1+2(1+y)]\)
\(−5[2m−(3m−1)]=4m−3m+2(5−2m)+1\)
- Answer
-
\(m=2\)
For the following problems, solve the literal equations for the indicated variable. When directed, find the value of that variable for the given values of the other variables.
Solve \(I = \dfrac{E}{R}\) for \(R\). Find the value of \(R\) when \(I = 0.005\) and \(E = 0.0035\).
Solve \(P = R - C\) for \(R\). Find the value of \(R\) when \(P = 27\) and \(C = 85\).
- Answer
-
\(R=112\)
Solve \(z = \dfrac{x-\hat{x}}{s}\) for \(x\). Find the value of \(x\) when \(z = 1.96, s = 2.5,\) and \(\hat{x} = 15\).
Solve \(F = \dfrac{S_{x}^{2}}{S_{y}^{2}}\) for \(S_{x}^{2} \cdot S_{x}^{2}\) represents a single quantity. Find the value of \(S_{x}^{2}\) when \(F = 2.21\) and \(S_{y}^{2} = 3.24\)
- Answer
-
\(S_{x}^{2} = F \cdot S_{y}^{2}\); \(S_{x}^{2} = 7.1604\)
Solve \(p = \dfrac{nRT}{V}\) for \(R\)
Solve \(x=4y+7\) for \(y\).
- Answer
-
\(y = \dfrac{x-7}{4}\)
Solve \(y=10x+16\) for \(x\).
Solve \(2x+5y=12\) for \(y\).
- Answer
-
\(y = \dfrac{-2x+12}{5}\)
Solve \(−9x+3y+15=0\) for \(y\).
Solve \(m = \dfrac{2n-h}{5}\) for \(n\).
- Answer
-
\(\dfrac{5m+h}{2}\)
Solve \(t = \dfrac{Q+6P}{8}\) for \(P\).
Exercises for Review
Simplify \((x+3)^2(x-2)^3(x-2)^4(x+3)\)
- Answer
-
\((x+3)^3(x-2)^7\)
Find the product. \((x-7)(x+7)\)
Find the product. \((2x-1)^2\).
- Answer
-
\(4x^2-4x+1\)
Solve the equation \(y−2=−2\).
Solve the equation \(\dfrac{4x}{5} = -3\)
- Answer
-
\(x = \dfrac{-15}{4}\)


