5.5: Application I - Translating from Verbal to Mathematical Expressions
- Page ID
- 49370
Translating from Verbal to Mathematical Expressions
To solve a problem using algebra, we must first express the problem algebraically. To express a problem algebraically, we must scrutinize the wording of the problem to determine the variables and constants that are present and the relationships among them. Then we must translate the verbal phrases and statements to algebraic expressions and equations.
To help us translate verbal expressions to mathematics, we can use the following table as a mathematics dictionary.
| Word or Phrase | Mathematical Operation |
| Sum, sum of, added to, increased by, more than, plus, and | \(+\) |
| Difference, minus, subtracted from, decreased by, less, less than | \(-\) |
| Product, the product of, of, muitiplied by, times | \(\cdot\) |
| Quotient, divided by, ratio | \(\div\) |
| Equals, is equal to, is, the result is, becomes | = |
| A number, an unknown quantity, an unknown, a quantity | \(x\) (or any symbol) |
Sample Set A
Translate the following phrases or sentences into mathematical expressions or equations.
\(\underbrace{\underbrace{\text { six }}_{6} \underbrace{\text { more than }}_{+} \underbrace{\text { a number }}_{x}}_{6+x} \text { . }\)
\(\underbrace{\underbrace{\text { Fifteen }}_{15} \underbrace{\text { minus }}_{15} \underbrace{\text { a number }}_{x}}_{15-x} \text { . }\)
\(\underbrace{\underbrace{\text { A quantity }}_{y} \underbrace{\text { less }}_{-} \underbrace{\text { eight. }}_{8}}_{y-8}\)
\(\underbrace{\underbrace{\text { Twice }}_{2 \cdot} \underbrace{\text { a number }}_{x} \underbrace{\text { is }}_{=} \underbrace{\operatorname{ten} .}_{10}}_{2 x=10}\)
\(\underbrace{\underbrace{\text { One half }}_{\dfrac{1}{2}} \underbrace{\text { of }}_{\cdot} \underbrace{\text { a number }}_{\mathbf{z}} \underbrace{\text { is }}_{=} \underbrace{\text { twenty }}_{20}}_{\dfrac{1}{2} z=20}\)
\(\underbrace{\underbrace{\text{Three}}_{3} \underbrace{\text{times}}_{\cdot} \underbrace{\text{a number}}_{y} \underbrace{\text{is}}_{=} \underbrace{\text{five}}_{5} \underbrace{\text{more than}}_{+} \underbrace{\text{twice}}_{2\cdot} \underbrace{\text{the same number}}_{y}}_{3y=5+2y}\)
Practice Set A
Translate the following phrases or sentences into mathematical expressions or equations.
Eleven more than a number.
- Answer
-
\(11+x\)
Nine minus a number.
- Answer
-
\(9−x\)
A quantity less twenty.
- Answer
-
\(x−20\)
Four times a number is thirty two.
- Answer
-
\(4x=32\)
One third of a number is six.
- Answer
-
\(\dfrac{x}{3} = 6\)
Ten times a number is eight more than five times the same number.
- Answer
-
\(10x=8+5x\)
Sometimes the structure of the sentence indicates the use of grouping symbols.
Sample Set B
Translate the following phrases or sentences into mathematical expressions or equations.
\(\underbrace{\underbrace{\text { A number divided by five, }}_{(\mathrm{x} \div 5)} \underbrace{\text { minus }}_{-} \underbrace{\text { ten, }}_{10} \underbrace{\text { is }}_{=} \underbrace{\text { fifteen. }}_{15}}_{\dfrac{x}{5}-10=15}\)
Commas set off terms
\(\begin{array}{c}
\underbrace{\text { Eight }}_{8} \underbrace{\text { divided by }}_{\div} \underbrace{\text { five more than a number }}_{(5+x)} \underbrace{\text { is }}_{=} \underbrace{\text { ten }}_{10} \\
\text { The wording indicates this is to be considered as a single quantity. } \\
\dfrac{8}{5+x}=10
\end{array}\)
\(\underbrace{\underbrace{\text { A number }}_{x} \underbrace{\text { multiplied by }}_{\text {, }} \underbrace{\text { ten more than itself }}_{(10+x)} \underbrace{\text { is }}_{=} \underbrace{\text { twenty. }}_{20}}_{x(10+x)=20}\)
A number plus one is divided by three times the number minus twelve and the result is four.
\(
\begin{aligned}
(x+1) \div(3 \cdot x-12) &=4 \\
\dfrac{x+1}{3 x-12} &=4
\end{aligned}
\)
Notice that since the phrase "three times the number minus twelve" does not contain a comma, we get the expression $3 x-12$. If the phrase had appeared as "three times the number, minus twelve," the result would have been
\(
\dfrac{x+1}{3 x}-12=4
\)
Some phrases and sentences do not translate directly. We must be careful to read them properly. The word from often appears in such phrases and sentences. The word from means "a point of departure for motion." The following translation will illustrate this use.
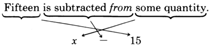
The word from indicates the motion (subtraction) is to begin at the point of "some quantity."
Eight less than some quantity. Notice that less than could be replaced with from.
\(x-8\)
Practice Set B
Translate the following phrases and sentences into mathematical expressions or equations.
A number divided by sixteen, plus one, is five.
- Answer
-
\(\dfrac{x}{16}+1 = 5\)
Seven times two more than a number is twenty-one.
- Answer
-
\(7(2+x) = 21\)
A number divided by two more than itself is zero.
- Answer
-
\(\dfrac{x}{2+x} = 0\)
A number minus five is divided by twice the number plus three and the result is seventeen.
- Answer
-
\(\dfrac{x-5}{2x+3} = 17\)
Fifty-two is subtracted from some quantity.
- Answer
-
\(x-52\)
An unknown quantity is subtracted from eleven and the result is five less than the unknown quantity.
- Answer
-
\(11−x=x−5\)
Exercises
For the following problems, translate the following phrases or sentences into mathematical expressions or equations.
A quantity less four.
- Answer
-
\(a−4\)
Eight more than a number.
A number plus seven.
- Answer
-
\(b+7\)
A number minus three.
Negative five plus an unknown quantity.
- Answer
-
\(−5+c\)
Negative sixteen minus some quantity.
Fourteen added to twice a number.
- Answer
-
\(2d+14\)
Ten added to three times some number.
One third minus an unknown quantity.
- Answer
-
\(\dfrac{1}{3}-e\)
Twice a number is eleven.
Four ninths of a number is twenty-one.
- Answer
-
\(\dfrac{4}{9}f = 21\)
One third of a number is two fifths.
Three times a number is nine more than twice the number.
- Answer
-
\(3g=2g+9\)
Five times a number is that number minus two.
Twice a number added to six results in thirty.
- Answer
-
\(2h+6=30\)
Ten times a number less four results in sixty-six.
A number less twenty-five is equal to \(3.019\).
- Answer
-
\(k−25=3.019\)
Seven more than some number is five more than twice the number.
When a number is divided by four, the result is sixty-eight.
- Answer
-
\(\dfrac{m}{4} = 68\)
Eleven fifteenths of two more than a number is eight.
One tenth of a number is that number less one.
- Answer
-
\(\dfrac{n}{10} = n-1\)
Two more than twice a number is one half the number less three.
A number is equal to itself plus four times itself.
- Answer
-
\(x=x+4x\)
Three fifths of a quantity added to the quantity itself is thirty-nine.
A number plus seven is divided by two and the result is twenty-two.
- Answer
-
\(\dfrac{Q+7}{2} = 22\)
Ten times a number minus one is divided by fourteen and the result is one.
A number is added to itself then divided by three. This result is then divided by three. The entire result is fifteen.
- Answer
-
\(\dfrac{\dfrac{r+r}{3}}{3} = 15\)
Ten divided by two more than a number is twenty-one.
Five divided by a number plus six is fourteen.
- Answer
-
\(\dfrac{5}{s+6} = 14\)
Twelve divided by twice a number is fifty-five.
Twenty divided by eight times a number added to one is nine.
- Answer
-
\(\dfrac{20}{8x}+1 = 9\)
A number divided by itself, plus one, results in seven.
A number divided by ten, plus four, results in twenty-four.
- Answer
-
\(\dfrac{v}{10} + 4 = 24\)
A number plus six, divided by two, is seventy-one.
A number plus six, divided by two, plus five, is forty-three.
- Answer
-
\(\dfrac{w+6}{2}+5 = 43\)
A number multiplied by itself added to five is thirty-one.
A quantity multiplied by seven plus twice itself is ninety.
- Answer
-
\(7y+2y=90\)
A number is increased by one and then multiplied by five times itself. The result is eighty-four.
A number is added to six and that result is multiplied by thirteen. This result is then divided by six times the number. The entire result is equal to fifty-nine.
- Answer
-
\(\dfrac{(z+16)13}{6z} = 59\)
A number is subtracted from ten and that result is multiplied by four. This result is then divided by three more than the number. The entire result is equal to six.
An unknown quantity is decreased by eleven. This result is then divided by fifteen. Now, one is subtracted from this result and five is obtained.
- Answer
-
\(\dfrac{x-11}{15}-1 = 5\)
Ten less than some number.
Five less than some unknown number.
- Answer
-
\(n−5\)
Twelve less than a number.
One less than an unknown quantity.
- Answer
-
\(m−1\)
Sixteen less than some number is forty-two.
Eight less than some unknown number is three.
- Answer
-
\(p−8=3\)
Seven is added to ten less than some number. The result is one.
Twenty-three is divided by two less than twice some number and the result is thirty-four.
- Answer
-
\(\dfrac{23}{2n-2} = 34\)
Exercises for Review
Supply the missing word. The point on a line that is associated with a particular number is called the of that number.
- Answer
-
graph
Supply the missing word. An exponent records the number of identical in a multiplication.
Write the algebraic definition of the absolute value of the number \(a\).
- Answer
-
\(|a|=\left\{\begin{array}{l}
a, \text { if } a \geq 0 \\
-a, \text { if } a<0
\end{array}\right.\)
Solve the equation \(4y+5=−3\).
Solve the equation \(2(3x+1)−5x=4(x−6)+17\).
- Answer
-
\(x=3\)
FFFF