6.3: Factoring a Monomial from a Polynomial
- Page ID
- 49374
The Factorization Process
We introduce the process of factoring a monomial from a polynomial by examining a problem: Suppose that \(12x^2+20x\) is the product and one of the factors is \(4x\). To find the other factor we could set up the problem this way:
\(4x \cdot () = 12x^2 + 20x\)
Since the product \(12x^2 + 20x\) consists of two terms, the expression multiplying \(4x\) must consist of two terms, since, by the distributive property
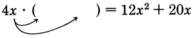
Now we see that this problem is simply an extension of finding the factors of a monomial.
\(\begin{array}{flushleft}
\text{1st term: }&4x()&=&12x^2&\text{2nd term: }&4x()&=&20x\\
&()&=&\dfrac{12x^2}{4x}&&()&=&\dfrac{20x}{4x}\\
&()&=&3x&&()&=&5\\
\end{array}\)
Thus, \(4x \cdot (3x+5) = 12x^2 + 20x\)
Usually, these divisions can be done mentally and the terms of the factor filled in directly.
Sample Set A
The product is \(3x^7-2x^6+4x^5-3x^4\) and one factor is \(x^4\). Find the other factor.
We have the problem: \(x^4\) times "what expression" yields \(3x^7-2x^6+4x^5-3x^4\)? Mathematically,
\(x^4 \cdot () = 3x^7-2x^6+4x^5-3x^4\)
Since there are four terms in the product, there must be four terms inside the parentheses. To find each of the four terms, we'll divide (mentally) each term of the product by \(x^4\). The resulting quotient will be the necessary term of the factor.
\(\begin{array}{flushleft}
\text{1st term: }&\dfrac{3x^7}{x^4}&=&3x^{7-4}=3x^3&\text{Place } 3x^3 \text{ into the 1sdt position in the ( )}\\
\text{2nd term: }&\dfrac{-2x^6}{x^4}&=&-2x^2&\text{Place } -2x^2 \text{ into the 2nd position in the ( )}\\
\text{3rd term: }&\dfrac{4x^5}{x^4}&=&4x&\text{Place } 4x \text{ into the 3rd position in the ( )}\\
\text{4th term: }&\dfrac{-3x^4}{x^4}&=&-3&\text{Place } -3 \text{ into the 4th position in the ( )}\\
\end{array}\)
Therefore, the other factor is \(3x^3-2x^2+4x-3\).
This result can be checked by applying the distributive property.
\(x^4 \cdot (3x^3-2x^2+4x-3) = 3x^7-2x^6+4x^5-3x^4\). Is this correct?
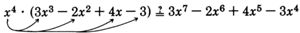
\(3x^{4+3} -2x^{4+2} + 4x^{4+1} = 3x^7 - 2x^6 + 4x^5 - 3x^4\) Is this correct?
\(3x^7 - 2x^6 + 4x^5 - 3x^4 = 3x^7 - 2x^6 + 4x^5 - 3x^4\) Yes, this is correct.
Thus,
\(x^4 \cdot (3x^3-2x^2+4x-3) = 3x^7-2x^6+4x^5-3x^4\)
Again, if the divisions can be performed mentally, the process can proceed very quickly.
The product is \(10x^3y^6 + 15x^3y^4 - 5x^2y^4\) and a factor is \(5x^2y^4\). Find the other factor.
\(5x^2y^4 \cdot ( ) = 10x^3y^6 + 15x^3y^4 - 5x^2y^4\)
Since there are three terms in the product, there must be three terms inside the parentheses. To find each of these three terms, we’ll divide each term of the product by \(5x^2y^4\).
\(\begin{array}{flushleft}
\text{1st term: }&\dfrac{10x^3y^6}{5x^2y^4}&=&2xy^2&\text{Place the } 2xy^2 \text{ into the 1st position in the ( )}\\
\text{2nd term: }&\dfrac{15x^3y^4}{5x^2y^4}&=&3x&\text{Place the } 3x \text{ into the 2nd position in the ( )}\\
\text{3rd term: }&\dfrac{-5x^2y^4}{5x^2y^4}&=&-1&\text{Place the } -1 \text{ into the 3rd position in the ( )}
\end{array}\)
The other factor is \(2xy^2 + 3x - 1\), and
\(5x^2y^4 \cdot (2xy^2 + 3x - 1) = 10x^3y^6 + 15x^3y^4 - 5x^2y^4\)
The product is \(-4a^2-b^3+2c\) and a factor is \(-1\). Find the other factor.
\(-1( ) = -4a^2-b^3+2c\)
Since there are three terms in the product, there must be three terms inside the parentheses. We will divide (mentally) each term of the product by \(-1\)
\(\begin{array}{flushleft}
\text{1st term: }&\dfrac{-4a^2}{-1}&=&4a^2&\text{Place } 4a^2 \text{ into the 1st position inside the ( )}\\
\text{2nd term: }&\dfrac{-b^3}{-1}&=&b^3&\text{Place } b^3 \text{ into the 2nd position inside the ( )}\\
\text{3rd term: }&\dfrac{2c}{-1}&=&-2c&\text{Place } -2c \text{ into the 3rd position inside the ( )}
\end{array}\)
The other factor is \(4a^2+b^3-2c\), and
\(-1(4a^2+b^3-2c) = -4a^2-b^3+2c\)
Without writing the \(-1\), we get
\(-(4a^2+b^3-2c) = -4a^2-b^3+2c\)
The product is \(-3a^2b^5 - 15a^3b^2 + 9a^2b^2\) and a factor is \(-3a^2b^2\). Find the other factor.
\(-3a^2b^2( ) = -3a^2b^5-15a^3b^2+9a^2b^2\)
Mentally dividing each term of the original trinomial by \(-3a^2b^2\), we get \(b^3 + 5a - 3\) as the other factor, and
\(-3a^2b^2(b^3 + 5a - 3) = -3a^2b^5 - 15a^3b^2 + 9a^2b^2\).
Practice Set A
The product is \(3x^2 - 6x\) and a factor is \(3x\). Find the other factor.
- Answer
-
\(x-2\)
The product is \(5y^4 + 10y^3 - 15y^2\) and a factor is \(5y^2\). Find the other factor.
- Answer
-
\(y^2 + 2y - 3\)
The product is \(4x^5y^3 - 8x^4y^4 + 16x^3y^5 + 24xy^7\) and a factor is \(4xy^3\). Find the other factor.
- Answer
-
\(x^4 - 2x^3y + 4x^2y^2 + 6y^4\)
The product is \(-25a^4-35a^2+5\) and a factor is \(-5\). Find the other factor.
- Answer
-
\(5a^4+7a^2-1\)
The product is \(-a^2 + b^2\) and a factor is \(-1\). Find the other factor.
- Answer
-
\(a^2-b^2\)
Exercises
For the following problems, the first quantity represents the product and the second quantity a factor. Find the other factor.
\(4x+10, 2\)
- Answer
-
\(2x+5\)
\(6y+18, 3\)
\(5x+25, 5\)
- Answer
-
\(x+5\)
\(16a+64, 8\)
\(3a^2 + 9a, 3a\)
- Answer
-
\(a+3\)
\(14b^2+16b, 2b\)
\(21x^2+28x, 7x\)
- Answer
-
\(3x+4\)
\(45y^2+50y, 5y\)
\(18a^2-4a, 2a\)
- Answer
-
\(9a−2\)
\(20a^2 - 12a, 4a\)
\(7x^2 - 14x, 7x\)
- Answer
-
\(x−2\)
\(6y^2 - 24y, 6y\)
\(8a^2 + 4a, 4a\)
- Answer
-
\(2a+1\)
\(26b^2 + 13b, 13b\)
\(9x^2 + 6x + 18, 6\)
- Answer
-
\(\dfrac{3}{2}x^2 + x + 3\)
\(12b^2 + 16b + 20, 4\)
\(21x^2 + 7x - 14, 7\)
- Answer
-
\(3x^2 + x - 2\)
\(35x^2 + 40x - 5, 5\)
\(14y^2 - 28y + 14, 14\)
- Answer
-
\(y^2 - 2y + 1\)
\(36a^2 - 16a + 12, 4\)
\(4y^2 - 10y - 12, 2\)
- Answer
-
\(2y^2 - 5y - 6\)
\(6b^2 - 6b - 3, 3\)
\(18x^3 + 20x, 2x\)
- Answer
-
\(9x^2 + 10\)
\(40y^3 + 24y, 4y\)
\(16x^3 - 12x^2, 4x^2\)
- Answer
-
\(4x−3\)
\(11x^3 - 11x + 11, 11\)
\(10a^3 + 12a^2 + 16a + 8, 2\)
- Answer
-
\(5a^3 + 6a^2 + 8a + 4\)
\(14b^3 + 16b^2 + 26b + 30, 2\)
\(8a^3 - 4a^2 - 12a + 16, 4\)
- Answer
-
\(2a^3 - a^2 - 3a + 4\)
\(25x^3 - 30x^2 + 15x - 10, 5\)
\(4x^6 + 16x^4 - 16x, 4x\)
- Answer
-
\(x^5 + 4x^3 - 4\)
\(9a^5 + 6a^5 - 18a^4 + 24a^2, 3a^2\)
\(10x^3 - 35x^2, 5x^2\)
- Answer
-
\(2x−7\)
\(12x^3y^5 + 20x^3y^2, 4x^3y^2\)
\(10a^4b^3 + 4a^3b^4, 2a^3b^3\)
- Answer
-
\(5a+2b\)
\(8a^3b^6c^8 + 12a^2b^7c^6 - 16a^2b^7c^5, 4a^2b^5c^5\)
\(4x^5y^4+x^2+x, x\)
- Answer
-
\(4x^4y^4+x+1\)
\(14a^5b^2 - 3a^4b^4 + 7a^3, a^3\)
\(64a^5b^3c^{11} + 56a^4b^4c^{10} - 48a^3b^5c^9 - 8a^3b^2c^5, 8a^3b^2c^5\)
- Answer
-
\(8a^2bc^6 + 7ab^2c^5 - 6b^3c^4 - 1\)
\(3h^3b^2 - 2h^6b^3 - 9h^2b + hb, hb\)
\(5a + 10, -5\)
- Answer
-
\(−a−2\)
\(6b+8, −2\)
\(8x^2 + 12x, -4x\)
- Answer
-
\(−2x−3\)
\(20a^2b^2-10a^2, -10a^2\)
\(a+b, −1\)
- Answer
-
\(−a−b\)
\(x+y, −1\)
\(a−b+c, −1\)
- Answer
-
\(−a+b−c\)
\(2x+4y−z, −1\)
\(−a−b−c, −1\)
- Answer
-
\(a+b+c\)
\(x^2-x+1, -1\)
Exercises for Review
How many \(4y^2\)'s are there in \(24x^2y^3\)?
- Answer
-
\(6x^2y\)
Find the product \((2y-3)^2\).
Solve \(2(2a−1)−a=7\).
- Answer
-
\(a=3\)
Given that \(3m^2n\) is a factor of \(12m^3n^4\), find the other factor.


