8.6: Adding and Subtracting Rational Expressions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Basic Rule
We are now in a position to study the process of adding and subtracting rational expressions. There is a most basic rule to which we must strictly adhere if we wish to conveniently add or subtract rational expressions.
To add or subtract rational expressions conveniently, they should have the same denominators.
Thus, to add or subtract two or more rational expressions conveniently, we must ensure that they all have the same denominator. The denominator that is most convenient is the LCD.
Fractions With The Same Denominator
To add (or subtract) two or more rational expressions with the same denominators, add (or subtract) the numerators and place the result over the LCD. Reduce if necessary. Symbolically,
\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}
\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}
Note that we combine only the numerators.
Sample Set A
Add or subtract the following rational expressions.
\begin{array}{flushleft} \dfrac{1}{6} + \dfrac{3}{6}&& \text{ The denominators are the same. Add the numerators.}\\ \dfrac{1}{6} + \dfrac{3}{6} &= \dfrac{1+3}{6} = \dfrac{4}{6} & \text{ Reduce }\\ \dfrac{1}{6} + \dfrac{3}{6} &= \dfrac{2}{3} \end{array}
\begin{array}{flushleft} \dfrac{5}{x} + \dfrac{8}{x} & \text{ The denominators are the same. Add the numerators }\\ \dfrac{5}{x} + \dfrac{5+8}{x} = \dfrac{13}{x} \end{array}
\begin{array}{flushleft} \dfrac{2ab}{y^2w} - \dfrac{5b}{y^2w} & \text{ The denominators are the same. Subtract the numerators }\\ \dfrac{2ab}{y^2w} - \dfrac{5b}{y^2w} = \dfrac{2ab - 5b}{y^2w} \end{array}
\begin{array}{flushleft} \dfrac{3x^2 + x + 2}{x-7} + \dfrac{x^2 - 4x + 1}{x-7} & \text{ The denominators are the same. Add the numerators}\\ \dfrac{3x^2 + x + 2}{x-7} + \dfrac{x^2 - 4x + 1}{x-7} &= \dfrac{3x^2 + x + 2 + x^2 - 4x + 1}{x-7}\\ &=\dfrac{4x^2 - 3x + 3}{x-7} \end{array}
\begin{array}{flushleft} \dfrac{5y + 3}{2y - 5} - \dfrac{2y + 4}{2y - 5} &&\text{ The denominators are the same. Subtract the numerators. }\\ &&\text{ But be careful to subtract the entire numerator. Use parentheses!}\\ \dfrac{5y + 3}{2y - 5} - \dfrac{2y + 4}{2y - 5} &= \dfrac{5y + 3 - (2y + 4)}{2y - 5}\\ & = \dfrac{5y + 3 - 2y - 4}{2y - 5}\\ & = \dfrac{3y - 1}{2y - 5} \end{array}
\text{ Note: } \dfrac{5y + 3}{2y - 5} - \dfrac{2y + 4}{2y - 5}
\text{ The term } -\dfrac{2y + 4}{2y - 5} \text{ could be written as}
+\dfrac{-(2y + 4)}{2y - 5} = \dfrac{-2y - 4}{2y - 5}
A common mistake is to write:
-\dfrac{2y + 4}{2y - 5} as \dfrac{-2y + 4}{2y - 5}
This is not correct, as the negative sign is not being applied to the entire numerator
\dfrac{3x^2 + 4x + 5}{(x+6)(x-2)} + \dfrac{2x^2 + x + 6}{x^2 + 4x - 12} - \dfrac{x^2 - 4x - 6}{x^2 + 4x - 12}
Factor the denominators to determine if they're the same:
\dfrac{3x^2 + 4x + 5}{(x+6)(x-2)} + \dfrac{2x^2 + x + 6}{(x+6)(x-2)} - \dfrac{x^2 - 4x - 6}{(x+6)(x-2)}
The denominators are the same. Combine the numerators being careful to note the negative sign.
\dfrac{3x^2 + 4x + 5 + 2x^2 + x + 6 - (x^2 - 4x + 6)}{(x+6)(x-2)}
\dfrac{3x^2 + 4x + 5 + 2x^2 + x + 6 - x^2 + 4x + 6}{(x+6)(x-2)}
\dfrac{4x^2 + 9x + 17}{(x+6)(x-2)}
Practice Set A
Add or Subtract the following rational expressions.
\dfrac{4}{9} + \dfrac{2}{9}
- Answer
-
\dfrac{2}{3}
\dfrac{3}{b} + \dfrac{2}{b}
- Answer
-
\dfrac{5}{b}
\dfrac{5x}{2y^2} - \dfrac{3x}{2y^2}
- Answer
-
\dfrac{x}{y^2}
\dfrac{x+y}{x-y} + \dfrac{2x + 3y}{x - y}
- Answer
-
\dfrac{3x + 4y}{x - y}
\dfrac{4x^2 - x + 4}{3x + 10} - \dfrac{x^2 + 2x + 5}{3x + 10}
- Answer
-
\dfrac{3x^2 - 3x - 1}{3x + 10}
\dfrac{x(x+1)}{x(2x + 3)} + \dfrac{3x^2 - x + 7}{2x^2 + 3x}
- Answer
-
\dfrac{4x^2 + 7}{x(2x + 3)}
\dfrac{4x + 3}{x^2 - x - 6} - \dfrac{8x - 4}{(x+2)(x-3)}
- Answer
-
\dfrac{-4x + 7}{(x+2)(x - 3)}
\dfrac{5a^2 + a - 4}{2a(a - 6)} + \dfrac{2a^2 + 3a + 4}{2a^2 - 12a} + \dfrac{a^2 + 2}{2a^2 - 12a}
- Answer
-
\dfrac{4a^2 + 2a + 1}{a(a-6)}
\dfrac{8x^2 + x - 1}{x^2 - 6x + 8} + \dfrac{2x^2 + 3x}{x^2 - 6x + 8} - \dfrac{5x^2 + 3x - 4}{(x-4)(x-2)}
- Answer
-
\dfrac{5x^2 + x + 3}{(x-4)(x-2)}
Fractions with Different Denominators
Sample Set B
Add or Subtract the following rational expressions.
\begin{array}{flushleft} \dfrac{4a}{3y} + \dfrac{2a}{8y^2}. & \text{The denominators are not the same. Find the LCD. By inspection, the LCD is} 9y^2\\ & \text{The denominator of the first rational expression has been multiplied by } 3y\\ \dfrac{?}{9y^2} + \dfrac{2a}{9y^2} & \text{so the numerator must be multiplied by } 3y\\ 4a \cdot 3y = 12ay\\ \dfrac{12ay}{9y^2} + \dfrac{2a}{9y^2} & \text{The denominators are now the same. Add the numerators.}\\ \dfrac{12ay + 2a}{9y^2} \end{array}
\begin{array}{flushleft} \dfrac{3b}{b + 2} + \dfrac{5b}{b-3} & \text{ The denominators are not the same. The LCD is } (b + 2)(b-3)\\ \dfrac{?}{(b+2)(b-3)} + \dfrac{?}{(b+2)(b-3)} & \text{ The denominator of the first rational expression has been multiplied by } b-3,\\ & \text{ so the numerator must be multiplied by } b-3.\\ 3b(b-3)\\ \dfrac{3b(b-3)}{(b+2)(b-3)} + \dfrac{?}{(b+2)(b-3)} & \text{ The denominator of the second rational expression has been multiplied by } b + 2,\\ & \text{ so the numerator must be multiplied by } b + 2.\\ 5b(b + 2).\\ \dfrac{3b(b-3)}{(b+2)(b-3)} + \dfrac{5b(b+2)}{(b+2)(b-3)} & \text{ The denominators are now the same. Add the numerators.} \end{array}
\begin{array}{flushleft} \dfrac{3b(b-3) + 5b(b + 2)}{(b-3)(b+2)} &= \dfrac{3b^2 - 9b + 5b^2 + 10b}{(b-3)(b+2)} & =\dfrac{8b^2 + b}{(b-3)(b+2)} \end{array}
\begin{array}{flushleft}
\dfrac{x+3}{x-1} + \dfrac{x-2}{4x + 4} & \text{ The denominators are not the same}\\
&\text{ Find the LCD}\\
\dfrac{x + 3}{x-1} + \dfrac{x - 2}{4(x+1)} & \text{ The LCD is } (x + 1)(x - 1)\\
\dfrac{?}{4(x+1)(x-1)} + \dfrac{?}{4(x+1)(x-1)} & \text{ The denominator of the first rational expression has been multiplied by } 4(x+1)\\
& \text{ the numerator must be multiplied by } 4(x+1)\\
4(x + 3)(x+1)\\
\dfrac{4(x+3)(x+1)}{4(x+1)(x-1)} + \dfrac{?}{4(x+1)(x-1)} & \text{ The denominator of the second rational expression has been multiplied by } (x-1)\\
& \text{ so the numerator must be multiplied by } x-1\\
(x-1)(x-2)\\
\dfrac{4(x+3)(x+1)}{4(x+1)(x-1)} + \dfrac{(x-1)(x-2)}{4(x+1)(x-2)} & \text{ The denominator are now the same.}\\
& \text{ Add the numerators}\\
\dfrac{4(x+3)(x+1) + (x-1)(x-2)}{4(x+1)(x-1)}\\
\dfrac{4(x^2 + 4x + 3) + x^2 - 3x + 2}{4(x + 1)(x-1)}
\end{array}
\dfrac{4x^2 + 16x + 12 + x^2 - 3x + 2}{4(x+1)(x-1)} = \dfrac{5x^2 + 13x + 14}{4(x+1)(x-1)}
\begin{array}{flushleft} \dfrac{x+5}{x^2 - 7x + 12} + \dfrac{3x - 1}{x^2 - 2x - 3} & \text{Determine the LCD}\\ \dfrac{x+5}{(x-4)(x-3)} + \dfrac{3x - 1}{(x-3)(x+1)} & \text{The LCD is } (x-4)(x-3)(x+1)\\ \dfrac{?}{(x-4)(x-3)(x+1)} + \dfrac{?}{(x-4)(x-3)(x+1)} & \text{ The first numerator must be multipled by } x + 1 \text{ and the second by } x-4\\ \dfrac{(x+5)(x+1)}{(x-4)(x-3)(x+1)} + \dfrac{(3x - 1)(x - 4)}{(x-4)(x-3)(x+1)} & \text{ The denominators are now the same. Add the numerators }\\ \dfrac{(x+5)(x+1) + (3x-1)(x-4)}{(x-4)(x-3)(x+1)}\\ \dfrac{x^2 + 6x + 5 = 3x^2 + -13x + 4}{(x-4)(x-3)(x+1)}\\ \dfrac{4x^2 - 7x + 9}{(x-4)(x-3)(x+1)} \end{array}
\begin{array}{flushleft} \dfrac{a+4}{a^2 + 5a + 6} - \dfrac{a-4}{a^2 - 5a - 24} & \text{Determine the LCD}\\ \dfrac{a+4}{(a+3)(a+2)} - \dfrac{a-4}{(a+3)(a-8)} & \text{ The LCD is } (a+3)(a+2)(a-8)\\ \dfrac{?}{(a+3)(a+2)(a-8)} - \dfrac{?}{(a+3)(a+2)(a-8)} & \text{ The first numerator must be multipled by } a-8 \text{ and the second by } a+2.\\ \dfrac{(a+4)(a-8)}{(a+3)(a+2)(a-8)} - \dfrac{(a-4)(a+2)}{(a+3)(a+2)(a-8)} & \text{ The denominators are now the same. Subtract the numerators.}\\ \dfrac{(a+4)(a-8) - (a-4)(a+2)}{(a+3)(a+2)(a-8)}\\ \dfrac{a^2 - 4a - 32 - (a^2 - 2a - 8)}{(a+3)(a+2)(a-8)}\\ \dfrac{a^2 - 4a - 32 - a^2 + 2a + 8}{(a+3)(a+2)(a-8)}\\ \dfrac{-2a-24}{(a+3)(a+2)(a-8)} & \text{ Factor } -2 \text{ from the numerator.}\\ \dfrac{-2(a+12)}{(a+3)(a+2)(a-8)} \end{array}
\begin{array}{flushleft} \dfrac{3x}{7-x} + \dfrac{5x}{x-7} && \text{ The denominators are nearly the same. They differ only in sign }\\ && \text{ Our technique is to factor } -1 \text{ from one of them}\\ \dfrac{3x}{7-x} = \dfrac{3x}{-(x-7)} &= \dfrac{-3x}{x-7}\\ \dfrac{3x}{7-x} + \dfrac{5x}{x-7} &= \dfrac{-3x}{x-7} + \dfrac{5x}{x-7}\\ &=\dfrac{-3x + 5x}{x-7}\\ &=\dfrac{2x}{x-7} \end{array}
Practice Set B
Add or Subtract the following rational expressions.
\dfrac{3x}{4a^2} + \dfrac{5x}{12a^3}
- Answer
-
\dfrac{9ax + 5x}{12a^3}
\dfrac{5b}{b+1} + \dfrac{3b}{b-2}
- Answer
-
\dfrac{8b^2 - 7b}{(b+1)(b-2)}
\dfrac{a-7}{a+2} + \dfrac{a-2}{a+3}
- Answer
-
\dfrac{2a^2 - 4a - 25}{(a+2)(a+3)}
\dfrac{4x + 1}{x+3} - \dfrac{x+5}{x-3}
- Answer
-
\dfrac{3x^2 - 19x - 18}{(x+3)(x-3)}
\dfrac{2y-3}{y} + \dfrac{3y + 1}{y + 4}
- Answer
-
\dfrac{5y^2 + 6y - 12}{y(y + 4)}
\dfrac{a-7}{a^2 - 3a + 2} + \dfrac{a + 2}{a^2 - 6a + 8}
- Answer
-
\dfrac{2a^2 - 10a + 26}{(a-2)(a-1)(a-4)}
\dfrac{6}{b^2 + 6b + 9} - \dfrac{2}{b^2 + 4b + 4}
- Answer
-
\dfrac{4b^2 + 12b + 6}{(b+3)^2(b+2)^2}
\dfrac{x}{x+4} - \dfrac{x-2}{3x-3}
- Answer
-
\dfrac{2x^2 - 5x + 8}{3(x+4)(x-2)}
\dfrac{5x}{4-x} + \dfrac{7x}{x-4}
- Answer
-
\dfrac{2x}{x-4}
Sample Set C
Combine the following rational expressions.
\begin{array}{flushleft} 3 + \dfrac{7}{x-1} & \text{Rewrite the expression}\\ \dfrac{3}{1} + \dfrac{7}{x-1} & \text{The LCD is } x-1\\ \dfrac{3(x-1)}{x-1} + \dfrac{7}{x-1} = \dfrac{3x-3}{x-1} + \dfrac{7}{x-1} &= \dfrac{3x-3+7}{x-1}\\ &=\dfrac{3x + 4}{x-1} \end{array}
\begin{array}{flushleft} 3y + 4 - \dfrac{y^2 - y +3}{y-6} & \text{Rewrite the expression.}\\ \dfrac{3y + 4}{1} - \dfrac{y^2 - y + 3}{y - 6} & \text{The LCD is } y-6\\ \dfrac{(3y+4)(y-6)}{y-6} - \dfrac{y^-y+3}{y-6} &= \dfrac{(3y+4)(y-6) - (y^2 - y +3)}{y-6}\\ &= \dfrac{3y^2 - 14y - 24 - y^2 + y - 3}{y-6}\\ &=\dfrac{2y^2 - 13y - 27}{y-6} \end{array}
Practice Set C
Simplify 8 + \dfrac{3}{x-6}
- Answer
-
\dfrac{8x - 45}{x-6}
Simplify 2a - 5 - \dfrac{a^2 + 2a - 1}{a+3}
- Answer
-
\dfrac{a^2 - a - 14}{a + 3}
Exercises
For the following problems, add or subtract the rational expressions.
\dfrac{3}{8} + \dfrac{1}{8}
- Answer
-
\dfrac{1}{2}
\dfrac{1}{9} + \dfrac{4}{9}
\dfrac{7}{10} - \dfrac{2}{5}
- Answer
-
\dfrac{3}{10}
\dfrac{3}{4} - \dfrac{5}{12}
\dfrac{3}{4x} + \dfrac{5}{4x}
- Answer
-
\dfrac{2}{x}
\dfrac{2}{7y} + \dfrac{3}{7y}
\dfrac{6y}{5x} + \dfrac{8y}{5x}
- Answer
-
\dfrac{14y}{5x}
\dfrac{9a}{7b} + \dfrac{3a}{7b}
\dfrac{15n}{2m} - \dfrac{6n}{2m}
- Answer
-
\dfrac{9n}{2m}
\dfrac{8p}{11q} - \dfrac{3p}{11q}
\dfrac{y+4}{y-6} + \dfrac{y+8}{y-6}
- Answer
-
\dfrac{2y + 12}{y - 6}
\dfrac{y-1}{y+4} + \dfrac{y+7}{y+4}
\dfrac{a+6}{a-1} + \dfrac{3a+5}{a-1}
- Answer
-
\dfrac{4a + 11}{a - 1}
\dfrac{5a + 1}{a+7} + \dfrac{2a - 6}{a + 7}
\dfrac{x + 1}{5x} + \dfrac{x + 3}{5x}
- Answer
-
\dfrac{2x + 4}{5x}
\dfrac{a - 6}{a + 2} + \dfrac{a - 2}{a+2}
\dfrac{b + 1}{b - 3} + \dfrac{b + 2}{b - 3}
- Answer
-
\dfrac{2b + 3}{b-3}
\dfrac{a + 2}{a - 5} - \dfrac{a+3}{a-5}
\dfrac{b + 7}{b-6} - \dfrac{b-1}{b-6}
- Answer
-
\dfrac{8}{b-6}
\dfrac{2b + 3}{b+1} - \dfrac{b-4}{b+1}
\dfrac{3y + 4}{y + 8} - \dfrac{2y - 5}{y + 8}
- Answer
-
\dfrac{y + 9}{y + 8}
\dfrac{2a - 7}{a - 9} + \dfrac{3a + 5}{a - 9}
\dfrac{8x - 1}{x + 2} - \dfrac{15x + 7}{x + 2}
- Answer
-
\dfrac{-7x - 8}{x + 2}
\dfrac{7}{2x^2} + \dfrac{1}{6x^3}
\dfrac{2}{3x} + \dfrac{4}{6x^2}
- Answer
-
\dfrac{2(x+1)}{3x^2}
\dfrac{5}{6y^3} - \dfrac{2}{18y^5}
\dfrac{2}{5a^2} - \dfrac{1}{10a^3}
- Answer
-
\dfrac{4a - 1}{10a^3}
\dfrac{3}{x+1} + \dfrac{5}{x-2}
\dfrac{4}{x-6} + \dfrac{1}{x-1}
- Answer
-
\dfrac{5(x-2)}{(x-6)(x-1)}
\dfrac{2a}{a+1} - \dfrac{3a}{a+4}
\dfrac{6y}{y + 4} + \dfrac{2y}{y + 3}
- Answer
-
\dfrac{2y(4y + 13)}{(y+4)(y+3)}
\dfrac{x-1}{x-3} + \dfrac{x + 4}{x-4}
\dfrac{x+2}{x-5} + \dfrac{x-1}{x+2}
- Answer
-
\dfrac{2x^2 - 2x + 9}{(x-5)(x+2)}
\dfrac{a+3}{a-3} - \dfrac{a+2}{a-2}
\dfrac{y+1}{y-1} - \dfrac{y+4}{y-4}
- Answer
-
\dfrac{-6y}{(y-1)(y-4)}
\dfrac{x-1}{(x+2)(x-3)} + \dfrac{x+4}{x-3}
\dfrac{y+2}{(y+1)(y+6)} + \dfrac{y-2}{y+6}
- Answer
-
\dfrac{y^2}{(y+1)(y+6)}
\dfrac{2a + 1}{(a+3)(a-3)} - \dfrac{a+2}{a+3}
\dfrac{3a + 5}{(a+4)(a-1)} - \dfrac{2a - 1}{a - 1}
- Answer
-
\dfrac{-2a^2 - 4a + 9}{(a+4)(a-1)}
\dfrac{2x}{x^2 - 3x + 2} + \dfrac{3}{x-2}
\dfrac{4a}{a^2 - 2a - 3} + \dfrac{3}{a + 1}
- Answer
-
\dfrac{7a - 9}{(a+1)(a-3)}
\dfrac{3y}{y^2 - 7y + 12} - \dfrac{y^2}{y-3}
\dfrac{x-1}{x^2 + 6x + 8} + \dfrac{x+3}{x^2 + 2x - 8}
- Answer
-
\dfrac{2(x^2 + x + 4)}{(x+2)(x-2)(x+4)}
\dfrac{a-4}{a^2 + 2a - 3} + \dfrac{a+2}{a^2 + 3a - 4}
\dfrac{x-1}{x^2 + 6x + 8} + \dfrac{x + 3}{x^2 + 2x - 8}
- Answer
-
\dfrac{2(x^2 + x + 4)}{(x+2)(x-2)(x+4)}
\dfrac{a-4}{a^2 + 2a - 3} + \dfrac{a + 2}{a^2 + 3a - 4}
\dfrac{b-3}{b^2 + 9b + 20} + \dfrac{b+4}{b^2 + b - 12}
- Answer
-
\dfrac{2b^2 + 3b + 29}{(b-3)(b+4)(b+5)}
\dfrac{y-1}{y^2 + 4y - 12} - \dfrac{y + 3}{y^2 + 6y - 16}
\dfrac{x+3}{x^2 + 9x + 13} - \dfrac{x - 5}{x^2 - 4}
- Answer
-
\dfrac{-x + 29}{(x-2)(x+2)(x+7)}
\dfrac{x-1}{x^2 - 4x + 3} + \dfrac{x + 3}{x^2 - 5x + 6} + \dfrac{2x}{x^2 - 3x + 2}
\dfrac{4x}{x^2 + 6x + 8} + \dfrac{3}{x^2 + x - 6} + \dfrac{x-1}{x^2 + x - 12}
- Answer
-
\dfrac{5x^4 - 3x^3 - 34x^2 + 34x - 60}{(x-2)(x+2)(x-3)(x+3)(x+4)}
\dfrac{y + 2}{y^2 - 1} + \dfrac{y-3}{y^2 - 3y - 4} - \dfrac{y + 3}{y^2 - 5y + 4}
\dfrac{a - 2}{a^2 - 9a + 18} + \dfrac{a - 2}{a^2 - 4a - 12} - \dfrac{a - 2}{a^2 - a - 6}
- Answer
-
\dfrac{(a+5)(a-2)}{(a+2)(a-3)(a-6)}
\dfrac{y-2}{y^2 + 6y} + \dfrac{y + 4}{y^2 + 5y - 6}
\dfrac{a + 1}{a^3 + 3a^2} - \dfrac{a + 6}{a^2 - a}
- Answer
-
\dfrac{-a^3 - 8a^2 - 18a - 1}{a^2(a+3)(a-1)}
\dfrac{4}{3b^2 - 12b} - \dfrac{2}{6b^2 - 6b}
\dfrac{3}{2x^5 - 4x^4} + \dfrac{-2}{8x^3 + 24x^2}
- Answer
-
\dfrac{-x^3 + 2x^2 + 6x + 18}{4x^4(x-2)(x+3)}
\dfrac{x + 2}{12x^3} + \dfrac{x + 1}{4x^2 + 8x - 12} - \dfrac{x + 3}{16x^2 - 32x + 16}
\dfrac{2x}{x^2 - 9} - \dfrac{x + 1}{4x^2 - 12x} - \dfrac{x-4}{8x^3}
- Answer
-
\dfrac{14x^4 - 9x^3 - 2x^2 + 9x - 36}{8x^3(x + 3)(x - 3)}
4 + \dfrac{3}{x+2}
8 + \dfrac{2}{x+6}
- Answer
-
\dfrac{8x + 50}{x + 6}
1 + \dfrac{4}{x-7}
3 + \dfrac{5}{x-6}
- Answer
-
\dfrac{3x - 13}{x - 6}
-2 + \dfrac{4x}{x+5}
-1 + \dfrac{3a}{a-1}
- Answer
-
\dfrac{2a + 1}{a - 1}
6 - \dfrac{4y}{y + 2}
2x + \dfrac{x^2 - 4}{x + 1}
- Answer
-
\dfrac{3x^2 + 2x - 4}{x + 1}
-3y + \dfrac{4y^2 + 2y - 5}{y + 3}
x + 2 + \dfrac{x^2 + 4}{x-1}
- Answer
-
\dfrac{2x^2 + x + 2}{x - 1}
b + 6 + \dfrac{2b + 5}{b-2}
\dfrac{3x - 1}{x - 4} - 8
- Answer
-
\dfrac{-5x + 31}{x - 4}
\dfrac{4y + 5}{y + 1} - 9
\dfrac{2y^2 + 11y - 1}{y + 4} - 3y
- Answer
-
\dfrac{-(y^2 + y + 1)}{y+4}
\dfrac{5y^2 - 2y + 1}{y^2 + y - 6} - 2
\dfrac{4a^3 + 2a^2 + a - 1}{a^2 + 11a + 28} + 3a
- Answer
-
\dfrac{7a^3 + 35a^2 + 85a - 1}{(a+7)(a+4)}
\dfrac{2x}{1-x} + \dfrac{6x}{x-1}
\dfrac{5m}{6-m} + \dfrac{3m}{m-6}
- Answer
-
\dfrac{-2m}{m-6}
\dfrac{-a+7}{8-3a} + \dfrac{2a + 1}{3a - 8}
Exercises For Review
Simplify (x^3y^2z^5)^6(x^2yz)^2
- Answer
-
x^{22}y^{14}z^{32}
Write 6a^{-3}b^4c^{-2}a^{-1}b^{-5}c^3 so that only positive exponents appear.
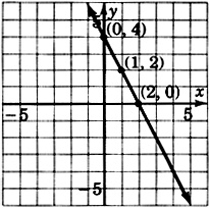
Construct the graph of y = -2x + 4
- Answer
-
Find the product \dfrac{x^2 - 3x - 4}{x^2 + 6x + 5} \cdot \dfrac{x^2 + 5x + 6}{x^2 - 2x - 8}
Replace N with the proper quantity: \dfrac{x+3}{x-5} = \dfrac{N}{x^2 - 7x + 10}
- Answer
-
(x+3)(x−2)


