11.5: Applications
- Page ID
- 49413
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Five-Step Method
When solving practical problems, it is often more convenient to introduce two variables rather than only one. Two variables should be introduced only when two relationships can be found within the problem. Each relationship will produce an equation, and a system of two equations in two variables will result.
We will use the five-step method to solve these problems.
- Introduce two variables, one for each unknown quantity.
- Look for two relationships within the problem. Translate the verbal phrases into mathematical expressions to form two equations.
- Solve the resulting system of equations.
- Check the solution.
- Write a conclusion.
Sample Set A (Number Problems)
The sum of two numbers is \(37\). One number is \(5\) larger than the other. What are the numbers?
Step 1:
Let \(x = \) smaller number.
Let \(y = \) larger number.
Step 2: There are two relationships.
a) The sum is \(37\)
\(x + y = 37\)
b) One is \(5\) larger than the other.
Step 3:
\(\left\{\begin{array}{r}
x + y = 37\\
y = x + 5
\end{array}\right.\)
We can easily solve this system by substitution. Substitute \(x + 5\) for \(y\) in equation 1.
\(\begin{aligned}
x + (x + 5) & = 37\\
x + x + 5 &= 37\\
2x + 5 &= 37\\
2x &= 32\\
x &= 16 & \text{ Then, } y = 16 + 5 = 21\\
x &= 16
\end{aligned}
Step 4: The sum if \(37\).
\(\begin{aligned}
x + y &= 37\\
16 + 21 &= 37 \text{ Is this correct? }\\
37 &= 37 \text{ Yes, this is correct. }
\end{aligned}\)
One is \(5\) larger than the other.
\(\begin{aligned}
y &= x + 5\\
21 &= 16 + 5\\
21 &= 21 \text{ Yes, this is correct. }
\end{aligned}\)
Step 5: The two numbers are \(16\) and \(21\).
Practice Set A
The difference of two numbers is 9, and the sum of the same two numbers is 19. What are the two numbers?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
- Answer
-
The two numbers are 14 and 5.
Value And Rate Problems: Coin Problems Problems And Mixture Problems
The problems in Sample Sets B and C are value problems. They are referred to as value problems because one of the equations of the system used in solving them is generated by considering a value, or rate, or amount times a quantity.
Sample Set B (Coin Problems)
A parking meter contains 27 coins consisting only of dimes and quarters. If the meter contains $4.35, how many of each type of coin is there?
Step 1:
Let \(D = \) number of dimes.
Let \(Q = \) number of quarters.
Step 2: There are two relationships.
a) There are 27 coins. \(D + Q = 27\).
b) Contribution due to dimes = 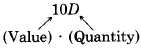
Contribution due to quarters = 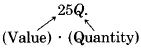
\(10D + 25Q = 435\)
Step 3:
\(\left\{\begin{array}{r}
D + Q = 27\\
10D + 25Q = 435
\end{array}\right.\)
We can solve this system using elimination by addition. Multiply both sides of equation (1) by \(-10\) and add.
\(\begin{array}{c}
-10 D-10 Q=-270 \\
10 D+25 Q=435 \\
\hline 15 Q=165 \\
Q=11
\end{array}\)
Then, \(D + 11 = 27\\
D = 16\)
\(D = 16, Q = 11\)
Step 4: 16 dimes and 11 quarters is 27 coins.
\(\begin{aligned}
10(16) + 11(25) &= 435 \text{ Is this correct? }\\
160 + 275 &= 435 \text{ Is this correct? }\\
435 &= 435 \text{ Yes, this is correct. }
\end{aligned}\)
The solution checks.
Step 5: There are 11 quarters and 16 dimes.
Practice Set B
A bag contains only nickels and dimes. The value of the collection is $2. If there are 26 coins in all, how many of each coin are there?
- Answer
-
There are 14 dimes and 12 nickels.
Sample Set C (Mixture Problems)
A chemistry student needs 40 milliliters (ml) of a 14% acid solution. She had two acid solutions, A and B, to mix together to form the 40 ml acid solution. Acid solution A is 10% acid and acid solution B is 20% acid. How much of each solution should be used?
Step 1:
Let \(x = \) number of ml is solution A.
Let \(y = \) number of ml of solution B.
Step 2: There are two relationships
a) The sum of the number of ml of the two solutions is 40.
\(x + y = 40\).
b) To determine the second equation, draw a picture of the situation
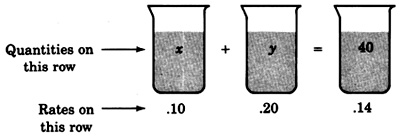
The equation follows directly from the drawing if we use the idea of amount times quantity.
Step 3: \(.10x + .20y = .14(40)\)
\(\left\{\begin{array}{r}
x + y = 40\\
.10x + .20y = .14(40)
\end{array}\right.\)
\(\left\{\begin{array}{r}
x + y = 40\\
.10x + .20y = .14(40)
\end{array}\right.\)
Solve this system by addition. First, eliminate decimals in equation 2 by multiplying both sides by 100.
\(\left\{\begin{array}{r}
x + y = 40\\
10x + 20y = 14(40)
\end{array}\right.\)
Eliminate \(x\) by multiplying equation 1 by \(-10\) and then adding.
\(\begin{array}{c}
-10 x-10 y=-400 \\
10 x+20 y=560 \\
\hline 10 y=160 \\
y=16
\end{array}\)
Then, \(x + 16 = 40\\
x = 24\)
\(x = 24, y = 16\)
Step 4: 24 ml and 16ml to add to 40ml.
\(\begin{aligned}
10(24) + 20(16) &= 560 \text{ Is this correct? }\\
240 + 320 &= 560 \text{ Is this correct? }\\
560 &= 560 \text{ Yes, this is correct. }
\end{aligned}\)
The solution checks.
Step 5: The student should use 24 ml of acid solution A and 16 ml of acid solution B.
Practice Set C
A chemistry student needs 60 ml of a 26% salt solution. He has two salt solutions, A and B, to mix together to form the 60 ml solution. Salt solution A is 30% salt and salt solution B is 20% salt. How much of each solution should be used?
- Answer
-
The student should use 36 ml of salt solution A and 24 ml of salt solution B.
Exercises
The sum of two numbers is 22. One number is 6 more than the other. What are the numbers?
- Answer
-
The two numbers are 14 and 8.
The sum of two numbers is 32. One number is 8 more than the other. What are the numbers?
The difference of two numbers is 12 and one number is three times as large as the other. Whatare the numbers?
- Answer
-
The two numbers are 18 and 6.
The difference of two numbers is 9 and one number is 10 times larger than the other. Whatare the numbers?
Half the sum of two numbers is 14 and half the difference is 2. What are the numbers?
- Answer
-
The numbers are 16 and 12.
One third of the sum of two numbers is 6 and one fifth of the difference is 2. What are the numbers?
A 14 pound mixture of grapes sells for $3.10. Type 1 grape sells for 25¢ a pound and type 2 grape sells for 20¢ a pound. How many pounds of each type of grape were used?
- Answer
-
6 pounds of Type 1 and 8 pounds of Type 2.
The cost of 80 liters of a blended cleaning solution is $28. Type 1 solution costs 20¢ a liter and type 2 solution costs 40¢ a liter. How many liters of each solution were used to form the blended solution?
The cost of 42 grams of a certain chemical compound is $14.40. Type 1 chemical costs 45¢ a gram and type 2 chemical costs 30¢ a gram. How many grams of each chemical were used to form the compound?
- Answer
-
12 grams of Type 1 and 30 grams of Type 2.
A play was attended by 342 people, some adults and some children. Admission for adults was $1.50 and for children 75¢. How many adults and how many children attended the play?
200 tickets were sold to a college’s annual musical performance. Tickets for students were $2.50 and for nonstudents $3.50. The total amount collected was $537. How many nonstudents purchased tickets for the performance?
- Answer
-
37 non-student tickets.
A chemistry student needs 22 ml of a 38% acid solution. She has two acid solutions, A and B, to mix together to form the solution. Acid solution A is 40% acid and acid solution B is 30% acid. How much of each solution should be used?
A chemistry student needs 50 ml of a 72% salt solution. He has two salt solutions, A and B, to mix together to form the solution. Salt solution A is 60% salt and salt solution B is 80% salt. How much of each solution should be used?
- Answer
-
30 ml of 80% solution; 20 ml of 60% solution.
A chemist needs 2 liters of an 18% acid solution. He has two solutions, A and B, to mix together to form the solution. Acid solution A is 10% acid and acid solution B is 15% acid. Can the chemist form the needed 18% acid solution? (Verify by calculation.) If the chemist locates a 20% acid solution, how much would have to be mixed with the 10% solution to obtain the needed 2-liter 18% solution?
A chemist needs 3 liters of a 12% acid solution. She has two acid solutions, A and B, to mix together to form the solution. Acid solution A is 14% acid and acid solution B is 20% acid. Can the chemist form the needed 12% solution? (Verify by calculation.) If the chemist locates a 4% acid solution, how much would have to be mixed with the 14% acid solution to obtain the needed 3-liter 12% solution?
- Answer
-
a) Cannot form 12% solution;
b) \(\dfrac{3}{5}\) liter of 4% solution.
A chemistry student needs 100 ml of a 16% acid solution. He has a bottle of 20% acid solution. How much pure water and how much of the 20% solution should be mixed to dilute the 20% acid solution to a 16% acid solution?
A chemistry student needs 1 liter of a 78% salt solution. She has a bottle of 80% salt solution. How much pure water and how much of the 80% salt solution should be mixed to dilute the 80% salt solution to a 78% salt solution?
- Answer
-
25 ml of pure water; 975 ml of 80% salt solution.
25 ml of pure water; 975 ml of 80% salt solution.
A child’s bank contains 78 coins. The coins are only pennies and nickels. If the value of the coins is $1.50, how many of each coin are there?
- Answer
-
18 nickels; 60 pennies.
Exercises For Review
Simplify \(\dfrac{x^{n + 6}}{x^2}\)
Find the product: \((3x - 5)^2\)
- Answer
-
\(9x^2 - 30x + 25\)
Find the difference: \(\dfrac{2x - 1}{x^2 + x - 6} - \dfrac{x + 2}{x^2 + 5x + 6}\)
Use substitution method to solve
\(\left\{\begin{array}{r}
4x - y = 3\\
2x - 5 = 15
\end{array}\right.\)
- Answer
-
\((0,−3)\)
Use the addition method to solve
\(\left\{\begin{array}{r}
3x + 4y = -7\\
4x - 5y = 1
\end{array}\right.\)


