11.4: Elimination by Addition
- Page ID
- 49412
The Properties Used in the Addition Method
Another method of solving a system of two linear equations in two variables is called the method of elimination by addition. It is similar to the method of elimination by substitution in that the process eliminates one equation and one variable. The method of elimination by addition makes use of the following two properties.
If \(A, B\), and \(C\) are algebraic expressions such that
\(A = B\) and \(C = D\)
Then: \(A + C = B + D\)
\(ax + (-ax) = 0\)
Property 1 states that if we add the left sides of two equations together and the right sides of the same two equations together, the resulting sums will be equal. We call this adding equations. Property 2 states that the sum of two opposites is zero.
The Addition Method
To solve a system of two linear equations in two variables by addition,
- Write, if necessary, both equations in general form, \(ax+by=c\).
- If necessary, multiply one or both equations by factors that will produce opposite coefficients for one of the variables.
- Add the equations to eliminate one equation and one variable.
- Solve the equation obtained in step 3.
- Do one of the following:
(a) Substitute the value obtained in step 4 into either of the original equations and solve to obtain the value of the other variable,
or
(b) Repeat steps 1-5 for the other variable. - Check the solutions in both equations.
- Write the solution as an ordered pair.
The addition method works well when the coefficient of one of the variables is 1 or a number other than 1.
Sample Set A
Solve the system
\(\left\{\begin{array}{r}
x-y = 2 \\
3x + y = 14
\end{array}\right.\)
Step 1: Both equations appear in the proper form.
Step 2: The coefficients of \(y\) are already opposites, \(1\) and \(-1\), so there is no need for a multiplication.
Step 3: Add the equations.
\(\begin{array}{c}
x-y=2 \\
3 x+y=14 \\
\hline 4 x+0=16
\end{array}\)
Step 4: Solve the equation \(4x = 16\)
\(4x = 16\\
x = 4\)
The problem is not solved yet; we still need the value of \(y\).
Step 5: Substitute \(x = 4\) into either of the original equations. We will use equation 1.
\(\begin{aligned}
4 - y &= 2 & \text{ Solve for } y\\
-y &= -2\\
y &= 2
\end{aligned}\)
We now have \(x = 4, y = 2\).
Step 6: Substitute \(x = 4\) and \(y = 2\) into both the original equations for a check.
(1)
\(\begin{aligned}
x - y &= 2\\
4 - 2 &= 2 \text{ Is this correct? }\\
2 &= 2 \text{ Yes, this is correct. }
\end{aligned}\)
(2)
\(\begin{aligned}
3x + y &= 14\\
3(4) + 2 &= 14\\
12 + 2 &= 14\\
14 &= 14 \text{ Yes, this is correct. }
\end{aligned}\)
Step 7: The solution is \((4, 2)\).
The two lines of this system intersect at \((4, 2)\).
Practice Set A
Solve each system by addition.
\(\left\{\begin{array}{r}
x + y = 6 \\
2x - y = 0
\end{array}\right.\)
- Answer
-
\((2, 4)\)
Solve the system
\(\left\{\begin{array}{r}
x + 6y = 8 \\
-x - 2y = 0
\end{array}\right.\)
- Answer
-
\((-4, 2)\)
Sample Set B
Solve the following systems using the addition method.
Solve
\(\left\{\begin{array}{r}
x + y = 6 \\
2x - y = 0
\end{array}\right.\)
Step 1: The equations are already in the proper form, \(ax + by = c\)
Step 2: If we multiply equation (2) by \(-3\), the coefficient of \(a\) will be opposites and become \(0\) upon addition, thus eliminating \(a\).
\(\left\{\begin{array} { l }
{ 6 a - 5 b = 1 4 } \\
{ - 3 ( 2 a + 2 b ) = - 3 ( 1 0 ) }
\end{array} \rightarrow \left\{\begin{array}{l}
6 a-5 b=14 \\
-6 a-6 b=30
\end{array}\right.\right.\)
Step 3: Add the equations.
\(\begin{array}{c}
6a - 5b = 14 \\
-6a - 6b = 30 \\
\hline 0 - 11b = 44
\end{array}\)
Step 4: Solve the equation \(-11b = 44\)
\(-11b = 44\\
b = -4\)
Step 5: Substitute \(b = -4\)
\(\begin{aligned}
2a + 2b &= -10\\
2a + 2(-4) &= -10 \text{ Solve for } a\\
2a - 8 &= -10\\
2a &= -2\\
a &= -1
\end{aligned}\)
We now have \(a = -1\) and \(b = -4\).
Step 6: Substitute \(a = -1\) and \(b = -4\) into both the original equations for a check.
(1)
\(\begin{aligned}
6a - 5b &= 14\\
6(-1) - 5(-4) &= 14\\
-6 + 20 &= 14\\
14 &= 14 \text{ Yes, this is correct. }
\end{aligned}\)
(2)
\(\begin{aligned}
2a + 2b &= -10\\
2(-1) + 2(-4) &= -10\\
-2 - 8 &= -10
-10 &= -10 \text{ Yes, this is correct. }
\end{aligned}\)
Step 7: the solution is \((-1, -4)\).
\(\left\{\begin{array}{r}
x + y = 6 \\
2x - y = 0
\end{array}\right.\)
Step 1: Rewrite the system in the proper form.
\(\left\{\begin{array}{r}
3x + 2y = -4 \\
4x - 5y = 10
\end{array}\right.\)
Step 2: Since the coefficients of \(y\) already have opposite signs, we will eliminate \(y\).
Multiply equation (1) by \(5\), the coefficient of \(y\) in equation 2.
Multiply equation (2) by \(2\), the coefficient of \(y\) in equation 1.
\(\left\{\begin{array} { l }
{ 5 ( 3 x + 2 y ) = 5 ( - 4 ) } \\
{ 2 ( 4 x - 5 y ) = 2 ( 1 0 ) }
\end{array} \rightarrow \left\{\begin{array}{l}
15 x+10 y=-20 \\
8 x-10 y=20
\end{array}\right.\right.\)
Step 3: Add the equations.
\(\begin{array}{c}
15x + 10y = -20 \\
8x - 10y = 20 \\
\hline 23x + 0 = 0
\end{array}\)
Step 4: Solve the equation \(23x = 0\)
\(23x = 0\\
x = 0\)
Step 5: Substitute \(x = 0\) into either of the original equations. We will use equation 1.
\(\begin{aligned}
3x + 2y &= -4\\
3(0) + 2y &= -4 \text{ Solve for } y\\
0 + 2y &= -4\\
y &= -2
\end{aligned}\)
Step 6: Substitution will show that these values check.
Step 7: The solution is \((0, -2)\)
Practice Set B
Solve each of the following systems using the addition method.
\(\left\{\begin{array}{r}
3x + y = 1 \\
5x + y = 3
\end{array}\right.\)
- Answer
-
\((1, -2)\)
\(\left\{\begin{array}{r}
x + 4y = 1 \\
x - 2y = -5
\end{array}\right.\)
- Answer
-
\((-3, 1)\)
\(\left\{\begin{array}{r}
2x + 3y = -10 \\
-x + 2y = -2
\end{array}\right.\)
- Answer
-
\((-2, -2)\)
\(\left\{\begin{array}{r}
5x - 3y = 1 \\
8x - 6y = 4
\end{array}\right.\)
- Answer
-
\((-1, -2)\)
\(\left\{\begin{array}{r}
3x - 5y = 9 \\
4x + 8y = 12
\end{array}\right.\)
- Answer
-
\((3, 0)\)
Addition And Parallel Or Coincident Lines
When the lines of a system are parallel or coincident, the method of elimination produces results identical to that of the method of elimination by substitution.
If computations eliminate all variables and produce a contradiction, the two lines of the system are parallel and the system is called inconsistent.
If computations eliminate all variables and produce an identity, the two lines of the system are coincident and the system is called dependent.
Sample Set C
Solve
\(\left\{\begin{array}{r}
2x - y = 1 \\
4x - 2y = 4
\end{array}\right.\)
Step 1: The equations are in the proper form
Step 2: We can eliminate \(x\) by multiplying equation (1) by \(-2\).
\(\left\{\begin{array} { c }
{ - 2 ( 2 x - y ) = - 2 ( 1 ) } \\
{ 4 x - 2 y = 4 }
\end{array} \quad \rightarrow \quad \left\{\begin{array}{c}
-4 x+2 y=-2 \\
4 x-2 y=4
\end{array}\right.\right.\)
Step 3: Add the equations
\(\begin{array}{c}
-4 x+2 y=-2 \\
4 x-2 y=4 \\
\hline 0+0=2 \\
0=2
\end{array}\)
This is false and is therefore a contradiction. The lines of this system are parallel. This system is inconsistent.
Solve
\(\left\{\begin{array}{r}
4x + 8y = 8 \\
3x + 6y = 6
\end{array}\right.\)
Step 1: The equations are in the proper form.
Step 2: We can eliminate \(x\) by multiplying equation (1) by \(-3\) and equation (2) by \(4\).
\(\left\{\begin{array} { c }
{ - 3 ( 4 x + 8 y ) = - 3 ( 8 ) } \\
{ 4 ( 3 x + 6 y ) = 4 ( 6 ) }
\end{array} \rightarrow \left\{\begin{array}{c}
-12 x-24 y=-24 \\
12 x+24 y=24
\end{array}\right.\right.\)
Step 3: Add the equations.
\(\begin{array}{c}
-12x - 24y = -24 \\
12x + 24y = 24 \\
\hline 0 + 0 = 0 \\
0=0
\end{array}\)
This is true and is an identity. The lines of this system are coincident.
This system is dependent.
Practice Set C
Solve each of the following systems using the addition method.
\(\left\{\begin{array}{r}
-x + 2y = 6 \\
-6x + 12y = 1
\end{array}\right.\)
- Answer
-
inconsistent
\(\left\{\begin{array}{r}
4x - 28y = -4 \\
x - 7y = -1
\end{array}\right.\)
- Answer
-
dependent
Exercises
For the following problems, solve the systems using elimination by addition.
\(\left\{\begin{array}{r}
x + y = 11 \\
x - y = -1
\end{array}\right.\)
- Answer
-
\((5, 6)\)
\(\left\{\begin{array}{r}
x + 3y = 13 \\
x - 3y = - 11
\end{array}\right.\)
\(\left\{\begin{array}{r}
3x - 5y = -4 \\
-4x + 5y = 2
\end{array}\right.\)
- Answer
-
\((2, 2)\)
\(\left\{\begin{array}{r}
2x - 7y = 1 \\
5x + 7y = -22
\end{array}\right.\)
\(\left\{\begin{array}{r}
-3x + 4y = -24 \\
3x - 7y = 42
\end{array}\right.\)
- Answer
-
\((0, -6)\)
\(\left\{\begin{array}{r}
8x + 5y = 3 \\
9x - 5y = -71
\end{array}\right.\)
\(\left\{\begin{array}{r}
-x + 2y = -6 \\
x + 3y = -4
\end{array}\right.\)
- Answer
-
\((2, -2)\)
\(\left\{\begin{array}{r}
4x + y = 0 \\
3x + y = 0
\end{array}\right.\)
\(\left\{\begin{array}{r}
x + y = -4 \\
-x - y = 4
\end{array}\right.\)
- Answer
-
dependent
\(\left\{\begin{array}{r}
-2x - 3y = -6\\
2x + 3y = 6
\end{array}\right.\)
\(\left\{\begin{array}{r}
3x + 4y = 7 \\
x + 5y = 6
\end{array}\right.\)
- Answer
-
\((1, 1)\)
\(\left\{\begin{array}{r}
4x - 2y = 2\\
7x + 4y = 26
\end{array}\right.\)
\(\left\{\begin{array}{r}
3x + y = -4 \\
5x - 2y = -14
\end{array}\right.\)
- Answer
-
\((-2, 2)\)
\(\left\{\begin{array}{r}
5x - 3y = 20 \\
-x + 6y = -4
\end{array}\right.\)
\(\left\{\begin{array}{r}
6x + 2y = -18 \\
-x + 5y = 19
\end{array}\right.\)
- Answer
-
\((-4, 3)\)
\(\left\{\begin{array}{r}
x - 11y = 17 \\
2x - 22y = 4
\end{array}\right.\)
\(\left\{\begin{array}{r}
-2x + 3y = 20 \\
-3x + 2y = 15
\end{array}\right.\)
- Answer
-
\((-1, 6)\)
\(\left\{\begin{array}{r}
-5x + 2y = -4 \\
-3x - 5y = 10
\end{array}\right.\)
\(\left\{\begin{array}{r}
-3x - 4y = 2\\
-9x - 12y = 6
\end{array}\right.\)
- Answer
-
dependent
\(\left\{\begin{array}{r}
3x - 5y = 28\\
-4x - 2y = -20
\end{array}\right.\)
\(\left\{\begin{array}{r}
6x - 3y = 3 \\
10x - 7y = 3
\end{array}\right.\)
- Answer
-
\((1, 1)\)
\(\left\{\begin{array}{r}
-4x + 12y = 0 \\
-8x + 16y = 0
\end{array}\right.\)
\(\left\{\begin{array}{r}
3x + y = -1 \\
12x + 4y = 6
\end{array}\right.\)
- Answer
-
inconsistent
\(\left\{\begin{array}{r}
8x + 5y = -23 \\
-3x - 3y = 12
\end{array}\right.\)
\(\left\{\begin{array}{r}
2x + 8y = 10 \\
3x + 12y = 15
\end{array}\right.\)
- Answer
-
dependent
\(\left\{\begin{array}{r}
4x + 6y = 8 \\
6x + 8y = 12
\end{array}\right.\)
\(\left\{\begin{array}{r}
10x + 2y = 2 \\
-15x - 3y = 3
\end{array}\right.\)
- Answer
-
inconsistent
\(\left\{\begin{array}{r}
x + \dfrac{3}{4}y = -\dfrac{1}{2} \\
\dfrac{3}{5}x + y = -\dfrac{7}{5}
\end{array}\right.\)
\(\left\{\begin{array}{r}
x + \dfrac{1}{3}y = \dfrac{4}{3} \\
-x + \dfrac{1}{6}y = \dfrac{2}{3}
\end{array}\right.\)
- Answer
-
\((0, 4)\)
\(\left\{\begin{array}{r}
8x - 3y = 25 \\
4x - 5y = -5
\end{array}\right.\)
\(\left\{\begin{array}{r}
-10x - 4y = 72 \\
9x + 5y = 39
\end{array}\right.\)
- Answer
-
\((-\dfrac{258}{7}, \dfrac{519}{7})\)
\(\left\{\begin{array}{r}
12x + 16y = -36 \\
-10x + 12y = 30
\end{array}\right.\)
\(\left\{\begin{array}{r}
25x - 32y = 14 \\
-50x + 64y = -28
\end{array}\right.\)
- Answer
-
dependent
Exercises For Review
Simplify and write \((2x^{-3}y^4)^5(2xy^{-6})^{-5}\) so that only positive exponents appear.
Simplify \(\sqrt{8} + 3\sqrt{50}\).
- Answer
-
\(17 \sqrt{2}\)
Solve the radical equation \(\sqrt{2x + 3} + 5 = 8\)
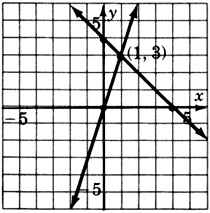
Solve by graphing:
\(\left\{\begin{array}{r}
x + y = 4 \\
3x - y = 0
\end{array}\right.\)
- Answer
-
\((1, 3)\)
Solve using the substitution method:
\(\left\{\begin{array}{r}
3x - 4y = -11 \\
5x + y = -3
\end{array}\right.\)


