11.3: Elimination by Substitution
- Page ID
- 49411
When Substitution Works Best
We know how to solve a linear equation in one variable. We shall now study a method for solving a system of two linear equations in two variables by transforming the two equations in two variables into one equation in one variable.
To make this transformation, we need to eliminate one equation and one variable. We can make this elimination by substitution.
When Substitution Works Best
The substitution method works best when either of these conditions exists:
- One of the variables has a coefficient of 1, or
- One of the variables can be made to have a coefficient of 1 without introducing fractions.
The Substitution Method
To solve a system of two linear equations in two variables,
- Solve one of the equations for one of the variables.
- Substitute the expression for the variable chosen in step 1 into the other equation.
- Solve the resulting equation in one variable.
- Substitute the value obtained in step 3 into the equation obtained in step 1 and solve to obtain the value of the other variable.
- Check the solution in both equations.
- Write the solution as an ordered pair.
Sample Set A
Solve the system
\(\left\{\begin{array}{r}
2x + 3y = 14 \\
3x + y = 7
\end{array}\right.\)
Step 1: Since the coefficient of \(y\) in equation 2 is \(1\), we will solve equation 2 for \(y\).
\(y = -3x + 7\)
Step 2: Substitute the expression \(-3x + 7\) for \(y\) in equation 1.
\(2x + 3(-3x + 7) = 14\)
Step 3: Solve the equation obtained in step 2.
\(\begin{aligned}
2x + 3(-3x + 7) &= 14\\
2x - 9x + 21 &= 14\\
-7x + 21 &= 14\\
-7x &= -7\\
x &= 1
\end{aligned}\)
Step 4: Substitute \(x = 1\) into the equation obtained in step 1, \(y = -3x + 7\).
\(\begin{aligned}
y &= -3(1) + 7\\
y &= -3 + 7\\
y &= 4
\end{aligned}\)
Step 5: Substitute \(x = 1, y = 4\) into each of the original equations for a check.
1)
\(\begin{aligned}
2 x+3 y &=14 \\
2(1)+3(4) &=14 \text { Is this correct? } \\
2+12 &=14 \text { Is this correct? } \\
14 &=14 \text { Yes, this is correct. }
\end{aligned}\)
2)
\(\begin{aligned}
3x + y &= 7\\
3(1) + (4) &= 7 \text{ Is this correct? }\\
3 + 4 &= 7 \text{ Is this correct? }\\
7 &= 7 \text{ Yes, this is correct. }
\end{aligned}\)
Step 6: The solution is \((1, 4)\). The point \((1, 4)\) is the point of intersection of the two lines of the system.
Practice Set A
Solve the system
\(\left\{\begin{array}{r}
5x - 8y = 18 \\
4x + y = 7
\end{array}\right.\)
- Answer
-
The point \((2, -1)\) is the point of intersection of the two lines.
Substitution And Parallel Lines
The following rule alerts us to the fact that the two lines of a system are parallel.
If computations eliminate all the variables and produce a contradiction, the two lines of a system are parallel, and the system is called inconsistent.
Sample Set B
Solve the system
\(\left\{\begin{array}{r}
2x - y = 1 \\
4x - 2y = 4
\end{array}\right.\)
Step 1: Solve equation for \(y\).
\(\begin{aligned}
2x - y &= 1\\
-y &= -2x + 1\\
y &= 2x - 1
\end{aligned}\)
Step 2: Substitute the expression \(2x - 1\) for \(y\) into equation 2.
\(4x - 2(2x - 1) = 4\)
Step 3: Solve the equation obtained in step 2.
\(\begin{aligned}
4x - 2(2x - 1) &= 4\\
4x - 4x + 2 &= 4\\
2 &\not= 4
\end{aligned}\)
Computations have eliminated all the variables and produce a contradiction. These lines are parallel.
This system is inconsistent.
Practice Set B
Solve the system
\(\left\{\begin{array}{r}
7x - 3y = 2 \\
14x - 6y = 1
\end{array}\right.\)
- Answer
-
Substitution produces \(4 \not= 1\), or \(\dfrac{1}{2} \not = 2\), a contradiction. These lines are parallel and the system is inconsistent.
Substitution And Coincident Lines
The following rule alerts us to the fact that the two lines of a system are coincident.
If computations eliminate all the variables and produce an identity, the two lines of a system are coincident and the system is called dependent.
Sample Set C
Solve the system
\(\left\{\begin{array}{r}
4x + 8y = 8 \\
3x + 6y = 6
\end{array}\right.\)
Step 1: Divide equation 1 by \(4\) and solve for \(x\).
\(\begin{aligned}
4x + 8y &= 8\\
x + 2y &= 2\\
x &= -2y + 2
\end{aligned}\)
Step 2: Substitute the expression \(-2y + 2\) for \(x\) in equation 2.
\(3(-2y + 2) + 6y = 6\)
Step 3: Solve the equation obtained in step 2.
\(\begin{aligned}
3(-2y + 2) + 6y &= 6\\
-6y + 6 + 6y &= 6\\
6 &= 6
\end{aligned}\)
Computations have eliminated all the variables and produced an identity. These lines are coincident.
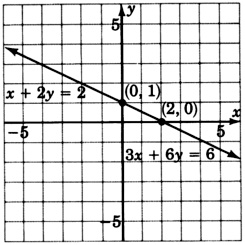
This system is dependent.
Practice Set C
Solve the system
\(\left\{\begin{array}{r}
4x + 3y = 1 \\
-8x - 6y = -2
\end{array}\right.\)
- Answer
-
Computations produce \(-2 = -2\), an identity. These lines are coincident and the system is dependent.
Systems in which a coefficient of one of the variables is not \(1\) or cannot be made to be \(1\) without introducing fractions are not well suited for the substitution method. The problem in Sample Set D illustrates this “messy” situation.
Sample Set D
Solve the system
\(\left\{\begin{array}{r}
3x + 2y = 1 \\
4x - 3y = 3
\end{array}\right.\)
Step 1: We will solve equation (1) for \(y\).
\(\begin{aligned}
3x + 2y &= 1\\
2y &= -3x + 1\\
y &= \dfrac{-3}{2}x + \dfrac{1}{2}
\end{aligned}\)
Step 2: Substitute the expression \(\dfrac{-3}{2}x + \dfrac{1}{2}\) for \(y\) in equation (2).
\(4x - 3(\dfrac{-3}{2}x + \dfrac{1}{2}) = 3\)
Step 3: Solve the equation obtained in step 2.
\(\begin{aligned}
4x - 3(\dfrac{-3}{2}x + \dfrac{1}{2}) &= 3 \text{ Multiply both sides by the LCD, } 2\\
4x + \dfrac{9}{2}x - \dfrac{3}{2} &= 3\\
8x + 9x - 3 &= 6\\
17x - 3 &= 6\\
17x &= 9\\
x &= \dfrac{9}{17}
\end{aligned}\)
Step 4: Substitute \(x = \dfrac{9}{17}\) into the equation obtained in step 1, \(y = \dfrac{-3}{2}x + \dfrac{1}{2}\)
\(y = \dfrac{-3}{2}(\dfrac{9}{17}) + \dfrac{1}{2}\\
y = \dfrac{-27}{34} + \dfrac{17}{34} = \dfrac{-10}{34} = \dfrac{-5}{17}\).
We now have \(x = \dfrac{9}{17}\) and \(y = \dfrac{-5}{17}\)\
Step 5: Substitution will show that these values of \(x\) and \(y\) check.
Step 6: The solution is \((\dfrac{9}{17}, \dfrac{-5}{17})\)
Practice Set D
Solve the system
\(\left\{\begin{array}{r}
9x - 5y = -4 \\
2x + 7y = -9
\end{array}\right.\)
- Answer
-
These lines intersect at the point \((−1,−1)\).
Exercises
For the following problems, solve the systems by substitution.
\(\left\{\begin{array}{r}
3x + 2y = 9 \\
y = -3x + 6
\end{array}\right.\)
- Answer
-
\((1, 3)\)
\(\left\{\begin{array}{r}
5x - 3y = -6 \\
y = -4x + 12
\end{array}\right.\)
\(\left\{\begin{array}{r}
2x + 2y = 0 \\
x = 3y - 4
\end{array}\right.\)
\(\left\{\begin{array}{r}
9x - 5y = -4 \\
2x + 7y = -9
\end{array}\right.\)
- Answer
-
\((-1, 1)\)
\(\left\{\begin{array}{r}
3x + 5y = 9 \\
x = 4y - 14
\end{array}\right.\)
\(\left\{\begin{array}{r}
-3x + y = -4\\
2x + 3y = 10
\end{array}\right.\)
- Answer
-
\((2,2)\)
\(\left\{\begin{array}{r}
-4x + y = -7 \\
2x + 5y = 9
\end{array}\right.\)
\(\left\{\begin{array}{r}
6x - 6 = 18 \\
x + 3y = 3
\end{array}\right.\)
- Answer
-
\((4, -\dfrac{1}{3})\)
\(\left\{\begin{array}{r}
-x - y = 5 \\
23x + y = 5
\end{array}\right.\)
\(\left\{\begin{array}{r}
-5x + y = 4 \\
10x - 2y = -8
\end{array}\right.\)
- Answer
-
Dependent (same line)
\(\left\{\begin{array}{r}
x + 4y = 1 \\
-3x - 12y = -1
\end{array}\right.\)
\(\left\{\begin{array}{r}
4x - 2y = 8 \\
6x + 3y = 0
\end{array}\right.\)
- Answer
-
\((1,−2)\)
\(\left\{\begin{array}{r}
2x + 3y = 12 \\
2x + 4y = 18
\end{array}\right.\)
\(\left\{\begin{array}{r}
3x - 9y = 6 \\
6x - 18y = 5
\end{array}\right.\)
- Answer
-
inconsistent (parallel lines)
\(\left\{\begin{array}{r}
-x + 4y = 8 \\
3x - 12y = 10
\end{array}\right.\)
\(\left\{\begin{array}{r}
x + y = -6 \\
x - y = 4
\end{array}\right.\)
- Answer
-
\((−1,−5)\)
\(\left\{\begin{array}{r}
2x + y = 0 \\
x - 3y = 0
\end{array}\right.\)
\(\left\{\begin{array}{r}
4x - 2y = 7 \\
y = 4
\end{array}\right.\)
- Answer
-
\((\dfrac{15}{4}, 4)\)
\(\left\{\begin{array}{r}
x + 6y = 11 \\
x = -1
\end{array}\right.\)
\(\left\{\begin{array}{r}
2x - 4y = 10 \\
3x = 5y + 12
\end{array}\right.\)
- Answer
-
\((−1,−3)\)
\(\left\{\begin{array}{r}
y + 7x + 4 = 0 \\
x = -7y + 28
\end{array}\right.\)
\(\left\{\begin{array}{r}
x + 4y = 0 \\
x + \dfrac{2}{3}y = \dfrac{10}{3}
\end{array}\right.\)
- Answer
-
\((4,−1)\)
\(\left\{\begin{array}{r}
x = 24 - 5y \\
x - \dfrac{5}{4}y = \dfrac{3}{2}
\end{array}\right.\)
\(\left\{\begin{array}{r}
x = 11 - 6y \\
3x + 18y = -33
\end{array}\right.\)
- Answer
-
inconsistent (parallel lines)
\(\left\{\begin{array}{r}
2x + \dfrac{1}{3}y = 4 \\
3x + 6y = 39
\end{array}\right.\)
\(\left\{\begin{array}{r}
\dfrac{4}{5}x + \dfrac{1}{2}y = \dfrac{3}{10} \\
\dfrac{1}{3} + \dfrac{1}{2}y = \dfrac{-1}{6}
\end{array}\right.\)
- Answer
-
\((1,−1)\)
Exercises For Review
Find the quotient: \(\dfrac{x^2 - x - 12}{x^2 - 2x - 15} \div \dfrac{x^2 - 3x - 10}{x^2 - 2x - 8}\)
- Answer
-
\(\dfrac{(x-4)^2}{(x-5)^2}\)
Find the difference: \(\dfrac{x + 2}{x^2 + 5x + 6} - \dfrac{x + 1}{x^2 + 4x + 3}\)
Simplify \(-\sqrt{81x^8y^5z^4}\)
- Answer
-
\(-9x^4y^2z^2 \sqrt{y}\)
Use the quadratic formula to solve \(2x^2 + 2x - 3 = 0\)
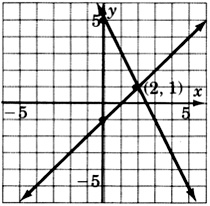
Solve by graphing:
\(\left\{\begin{array}{r}
x - y = 1 \\
2x + y = 5
\end{array}\right.\)
- Answer
-
\((2,1)\)
