11.2: Solutions by Graphing

Last updated
Save as PDF

Page ID: 49410

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Systems of Equations

Systems of Equations

A collection of two linear equations in two variables is called a system of linear equations in two variables, or more briefly, a system of equations. The pair of equations

$\left\{\begin{array}{r}
5 x-2 y=5 \\
x+y=8
\end{array}\right.$

is a system of equations. The brace { is used to denote that the two equations occur together (simultaneously).

Solution to A System of Equations

Solution to a System

We know that one of the infinitely many solutions to one linear equation in two variables is an ordered pair. An ordered pair that is a solution to both of the equations in a system is called a solution to the system of equations. For example, the ordered pair $(3, 5)$ is a solution to the system

$\left\{\begin{array}{r}
5 x-2 y=5 \\
x+y=8
\end{array}\right.$

since $(3, 5)$ is a solution to both equations.

$\begin{array}{flushleft}
5x - 2y &= 5 & & x + y &= 8\\
5(3) - 2(5) &= 5 & \text{ Is this correct? } & 3 + 5 &= 8 & \text{ Is this correct? }\\
15 - 10 &= 5 & \text{ Is this correct? } & 8 &= 8 & \text{ Yes, this is correct. }\\
5 &= 5 & \text{ Yes, this is correct. }
\end{array}$

Graphs of Systems of Equations

One method of solving a system of equations is by graphing. We know that the graph of a linear equation in two variables is a straight line. The graph of a system will consist of two straight lines. When two straight lines are graphed, one of three possibilities may result.

Example $\PageIndex{1}$

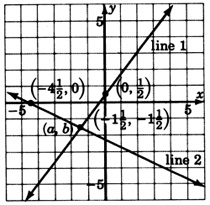
The lines intersect at the point $a, b$. This point $(a, b)$ is the solution to the corresponding system.

$A graph of two lines; 'line one' and 'line two,' intersecting at a point labeled with coordinates (a, b) and with a second label with x-coordinate negative one and one-half, and y-coordinate negative one and one-half. Line one is passing through a point with coordinates zero, one over two, and line two is passing through a point with coordinates negative four and one half, zero.$

Example $\PageIndex{2}$

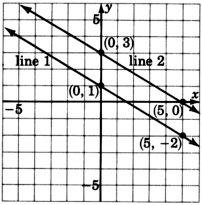
The lines are parallel. They do not intersect. The system has no solution.

$A graph of two parallel lines; 'Line one' and 'Line two'. Line one is passing through two points with the coordinates zero, one, and five, negative two. Line two is passing through two points with the coordinates zero, three, and five, zero.$

Example $\PageIndex{3}$

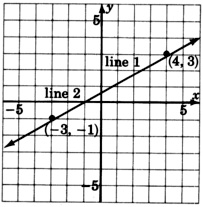
The lines are coincident (one on the other). They intersect at infinitely many points. The system has infinitely many solutions.

$A graph of two conincident lines; 'Line one' and 'Line two'. The lines are passsing through the same two points with the coordinates negative three, negative one, and four, three. Since the lines are coincident lines they have the same graph.$

Independent, Inconsistent, and Dependent Systems

Independent Systems

Systems in which the lines intersect at precisely one point are called independent systems. In applications, independent systems can arise when the collected data are accurate and complete. For example,

The sum of two numbers is 10 and the product of the two numbers is 21. Find the numbers.

In this application, the data are accurate and complete. The solution is 7 and 3.

Inconsistent Systems

Systems in which the lines are parallel are called inconsistent systems. In applications, inconsistent systems can arise when the collected data are contradictory. For example,

The sum of two even numbers is 30 and the difference of the same two numbers is 0. Find the numbers.

The data are contradictory. There is no solution to this application.

Dependent Systems

Systems in which the lines are coincident are called dependent systems. In applications, dependent systems can arise when the collected data are incomplete. For example.

The difference of two numbers is 9 and twice one number is 18 more than twice the other.

The data are incomplete. There are infinitely many solutions.

The Method of Solving A System Graphically

The Method of Solving a System Graphically

To solve a system of equations graphically: Graph both equations.

If the lines intersect, the solution is the ordered pair that corresponds to the point of intersection. The system is independent.
If the lines are parallel, there is no solution. The system is inconsistent.
If the lines are coincident, there are infinitely many solutions. The system is dependent.

Sample Set A

Solve each of the following systems by graphing.

Example $\PageIndex{4}$

$\left\{\begin{array}{r}
2x + y = 5 \\
x+y=2
\end{array}\right.$

Write each equation in slope-intercept form.

1) $y = 2x + 5$

2) $y = -x + 2$

Graph each of these equations:

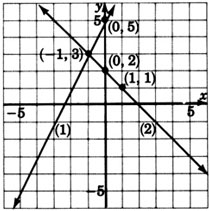
$A graph of two lines; ‘one’ and ‘two.’ The lines are intersecting at a point with coordinates negative one, three. Line one is passing through a point with coordinates zero, five. Line two is passing through two points with coordinates zero, two, and one, one.$

The lines appear to intersect at the point $(-1, 3)$. The solution to this system is $(-1, 3)$, or

$x = -1, y = 3$.

Check: Substitute $x - 01, y = 3$ into each equation.

$\begin{array}{flushleft}
-2x + y &= 5\\
-2(-1) + 3 &= 5 & \text{ Is this correct? }\\
2 + 3 &= 5 & \text{ Is this correct? } \\
5 &= 5 & \text{ Yes, this is correct }
\end{array}$

$\begin{array}{flushleft}
x + y &= 2\\
-1 + 3 &= 2 & \text{ Is this correct? }\\
2 &= 2 & \text{ Yes, this is correct. }
\end{array}$

Example $\PageIndex{5}$

$\left\{\begin{array}{r}
-x + y = -1 \\
-x + y = 2
\end{array}\right.$

Write each equation in slope-intercept form.

1) $y = 2x + 5$

2) $y = -x + 2$

Graph each of these equations.

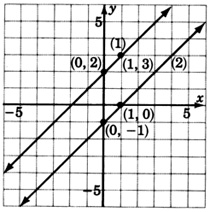
$A graph of two parallel line; 'one' and 'two'. Line one is passing through two points with the coordinates zero, two, and one, three. Line two is passing through two points with the coordinates zero, negative one, and one, zero.$

These lines are parallel. This system has no solution. We denote this fact by writing inconsistent.

We are sure that these lines are parallel because we notice that they have the same slope, $m = 1$ for both lines. The lines are not coincident because the y-intercepts are different.

Example $\PageIndex{6}$

$\left\{\begin{array}{r}
-2x + 3y -2 \\
-6x + 9y = -6
\end{array}\right.$

Write each equation in slope-intercept form.

1) $y = \dfrac{2}{3}x - \dfrac{2}{3}$

2) $y = \dfrac{2}{3}x - \dfrac{2}{3}$

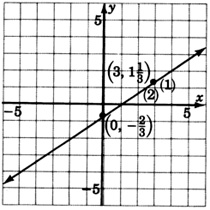
$A graph of two conincident lines; 'one' and 'two'. The lines are passsing through the same two points with the coordinates zero, negative two over three, and three, one and one third. Since the lines are coincident, they have the same graph.$

Both equations are the same. This system has infinitely many solutions. We write dependent.

Practice Set A

Solve each of the following systems by graphing. Write the ordered pair solution or state that the system is inconsistent, or dependent.

Practice Problem $\PageIndex{1}$

$\left\{\begin{array}{r}
2x + y = 1 \\
-x + y = -5
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Answer

$x=2,y=−3$

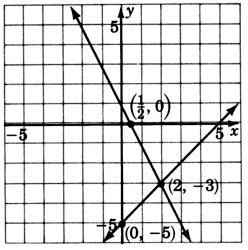
$A graph of two lines intersecting at a point with the coordinates two, negative three. One of the lines is passing through a point with the coordinates one over two, zero, and the other line is passing through a point with the coordinates zero, negative five.$

Practice Problem $\PageIndex{2}$

$\left\{\begin{array}{r}
-2x + 3y = 6 \\
6x - 9y = -18
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Answer

dependent

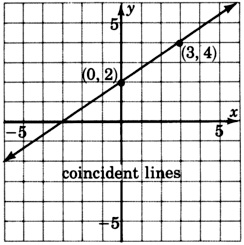
$A graph of two coincident lines passing through the same two points with the coordinates zero, two, and three, four. Since the lines are coincident, they have the same graph. The graph is labeled as 'coincident lines.'$

Practice Problem $\PageIndex{3}$

$\left\{\begin{array}{r}
3x + 5y = 15 \\
9x + 15y = 15
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Answer

inconsistent

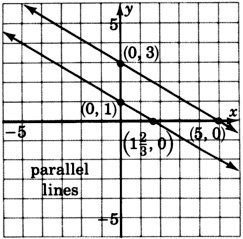
$A A graph of two parallel lines. One of the lines is passing through two points with coordinates zero, one and one and two third, zero. The other line is passing through two points with coordinates zero, three, and five, zero. The graph is labeled as 'parallel lines.'$

Practice Problem $\PageIndex{4}$

$\left\{\begin{array}{r}
y = -3 \\
x + 2y = -4
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Answer

$x=2,y=−3$

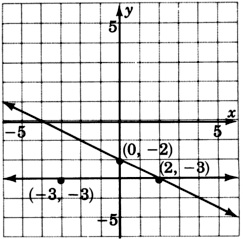
$A graph of two lines intersecting at a point with the coordinates two, negative three. One of the lines is passing through a point with the coordinates one zero, negative two. The other line is parallel to x axis, and is passing through a point with the coordinates negative three, negative three.$

Exercises

For the following problems, solve the systems by graphing. Write the ordered pair solution, or state that the system is inconsistent or dependent.

Exercise $\PageIndex{1}$

$\left\{\begin{array}{r}
x + y = -5 \\
-x + y = 1
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Answer

$(−3,−2)$

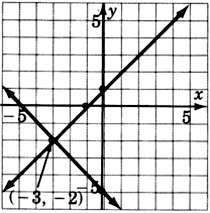
$A graph of two lines intersecting at a point with coordinates negative three, negative two. One of the lines is passing through a point with coordinates zero, negative five and, the other line is passing through two points with coordinates negative one, zero; and zero, one.$

Exercise $\PageIndex{2}$

$\left\{\begin{array}{r}
x + y = 4 \\
x + y = 0
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Exercise $\PageIndex{3}$

$\left\{\begin{array}{r}
-3x + y = 5 \\
-x + y = 3
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Answer

$(−1,2)$

$A graph of two lines intersecting at a point with coordinates negative one, two. One of the lines is passing through a point with coordinates zero, five, and the other line is passing through two points with coordinates zero, three; and one, four.$

Exercise $\PageIndex{4}$

$\left\{\begin{array}{r}
x - y = -6 \\
x + 2y = 0
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Exercise $\PageIndex{5}$

$\left\{\begin{array}{r}
3x + y = 0 \\
4x - 3y = 12
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Answer

$(\dfrac{12}{13}, -\dfrac{36}{13})$

$A graph of two lines intersecting at a point with coordinates twelve over thirteen, negative thirty-six over thirteen. One of the lines is passing through a point with coordinates zero, zero and the other line is passing through two points with coordinates zero, negative four; and three, zero.$

Exercise $\PageIndex{6}$

$\left\{\begin{array}{r}
-4x + y = 7 \\
-3x + y = 2
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Exercise $\PageIndex{7}$

$\left\{\begin{array}{r}
2x + 3y = 6 \\
3x + 4y = 6
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

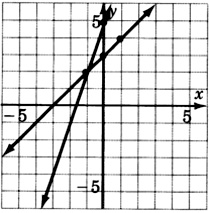
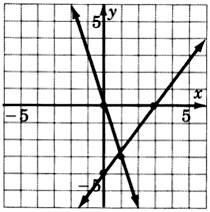
Answer

These coordinates are hard to estimate. This problem illustrates that the graphical method is not always the most accurate.

$(−6,6)$

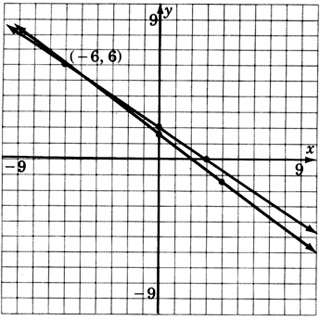
$A graph of two lines intersecting at a point with coordinates negative six, six. One of the lines is passing through a point with coordinates zero, three over two and the other line is passing through two points with coordinates zero, two; and three, zero.$

Exercise $\PageIndex{8}$

$\left\{\begin{array}{r}
x + y = -3 \\
4x + 4y = -12
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Exercise $\PageIndex{9}$

$\left\{\begin{array}{r}
2x - 3y = 1 \\
4x - 6y = 4
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Answer

inconsistent

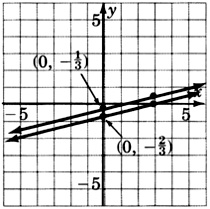
$A graph of two parallel lines. One of the lines is passing through two points with coordinates zero, negative two over three and three, zero. The other line is passing through a point with coordinates zero, negative one over three.$

Exercise $\PageIndex{10}$

$\left\{\begin{array}{r}
x + 2y = 3 \\
-3x - 6y = -9
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Exercise $\PageIndex{11}$

$\left\{\begin{array}{r}
x - 2y = 6 \\
3x - 6y = 18
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Answer

dependent

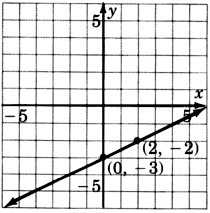
$A graph of two coincident lines passing through the same two points with coordinates zero, negative three; and two, negative two. Since the lines are coincident, they have the same graph.$

Exercise $\PageIndex{12}$

$\left\{\begin{array}{r}
2x + 3y = 6 \\
-10x - 15y = 30
\end{array}\right.$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Exercises For Review

Exercise $\PageIndex{13}$

Express $0.000426$ in scientific notation.

Answer: $4.26 + 10^{-4}$

Exercise $\PageIndex{14}$

Find the product $(7x - 3)^2$.

Exercise $\PageIndex{15}$

Supply the missing word. The _____ of a line is a measure of the steepness of the line.

Answer: slope

Exercise $\PageIndex{16}$

Supply the missing word. An equation of the form $ax^2 + bx + c = 0$, a \not = 0\), is called a equation.

Exercise $\PageIndex{17}$

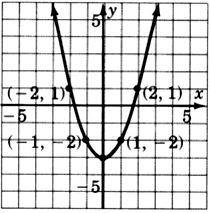
Construct the graph of the quadratic equation $y = x^2 - 3$

$An xy coordinate plane with gridlines, labeled negative five and five with increments of one unit for both axes.$

Answer: $A graph of a parabola passing through four points with coordinates negative two, one; negative one, negative two; one, negative two; and two, one.$

Search

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

The Method of Solving a System Graphically

Example \(\PageIndex{4}\)

Example \(\PageIndex{5}\)

Example \(\PageIndex{6}\)

Practice Problem \(\PageIndex{1}\)

Practice Problem \(\PageIndex{2}\)

Practice Problem \(\PageIndex{3}\)

Practice Problem \(\PageIndex{4}\)

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)