9.1: Extracting Square Roots
- Page ID
- 18382
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Solve quadratic equations by extracting square roots.
Extracting Square Roots
Recall that a quadratic equation is in standard form if it is equal to 0:
\[a x^{2}+b x+c=0\]
where a, b, and c are real numbers and \(a\neq 0\). A solution to such an equation is called a root. Quadratic equations can have two real solutions, one real solution, or no real solution. If the quadratic expression on the left factors, then we can solve it by factoring. A review of the steps used to solve by factoring follow:
Step 1: Express the quadratic equation in standard form.
Step 2: Factor the quadratic expression.
Step 3: Apply the zero-product property and set each variable factor equal to 0.
Step 4: Solve the resulting linear equations.
For example, we can solve \(x^{2}-4=0\) by factoring as follows:
The two solutions are −2 and 2. The goal in this section is to develop an alternative method that can be used to easily solve equations where b = 0, giving the form
\[a x^{2}+c=0\]
The equation \(x^{2}-4=0\) is in this form and can be solved by first isolating \(x^{2}\).
If we take the square root of both sides of this equation, we obtain the following:
\(\begin{aligned} \sqrt{x^{2}} &=\sqrt{4} \\|x| &=2 \end{aligned}\)
Here we see that \(x=-2\) and \(x=2\) are solutions to the resulting equation. In general, this describes the square root property; for any real number k,
\[\text{If}\:x^{2}=k, \text { then } x=\pm \sqrt{k}\]
The notation “±” is read “plus or minus” and is used as compact notation that indicates two solutions. Hence the statement \(x=\pm \sqrt{k}\) indicates that \(x= - \sqrt{k}\)or \(x= + \sqrt{k}\). Applying the square root property as a means of solving a quadratic equation is called extracting the roots.
Solve:
\(x^{2}-25=0\)
Solution:
Begin by isolating the square.
Next, apply the square root property.
\(\begin{aligned} x^{2} &=25 \\ x &=\pm \sqrt{25} \\ x &=\pm 5 \end{aligned}\)
Answer:
The solutions are −5 and 5. The check is left to the reader.
Certainly, the previous example could have been solved just as easily by factoring. However, it demonstrates a technique that can be used to solve equations in this form that do not factor.
Solve:
\(x^{2}-5=0\)
Solution:
Notice that the quadratic expression on the left does not factor. We can extract the roots if we first isolate the leading term, \(x^{2}\).
Apply the square root property.
\(x=\pm \sqrt{5}\)
For completeness, check that these two real solutions solve the original quadratic equation. Generally, the check is optional.
\(\begin{array}{rlrl}{\text { Check } x=-\sqrt{5}} & {\text { Check } x=\sqrt{5}} \\ {x^{2}-5=0} & {x^{2}-5=0} \\ {(\color{OliveGreen}{-\sqrt{5}}\color{black}{)}^{2}-5=0} & {(\color{OliveGreen}{\sqrt{5}}\color{black}{)}^{2}-5=0} \\ {5-5=0} & {5-5=0} \\ {0=0 \color{Cerulean}{\checkmark}} & {0=0\color{Cerulean}{\checkmark}}\end{array}\)
Answer:
The solutions are \(-\sqrt{5}\) and \(\sqrt{5}\).
Solve
Solution
Begin by isolating \(x^{2}\).
Apply the square root property and then simplify.
\(\begin{array}{l}{x=\pm \sqrt{\frac{45}{4}}} \\ {x=\pm \frac{\sqrt{9 \cdot 5}}{\sqrt{4}}} \\ {x=\pm \frac{3 \sqrt{5}}{2}}\end{array}\)
Answer:
The solutions are \(-\frac{3 \sqrt{5}}{2}\) and \(\frac{3 \sqrt{5}}{2}\).
Sometimes quadratic equations have no real solution.
Solve:
\(x^{2} + 9 =0\)
Solution
Begin by isolating \(x^{2}\).
After applying the square root property, we are left with the square root of a negative number. Therefore, there is no real solution to this equation.
Answer:
No real solution
Reverse this process to find equations with given solutions of the form ±k.
Example \(\PageIndex{5}\)
Find an equation with solutions \(-2 \sqrt{3}\) and \(2 \sqrt{3}\).
Solution:
Begin by squaring both sides of the following equation:
\(\begin{array}{l}{x=\pm 2 \sqrt{3}} \\ {x^{2}=( \pm 2 \sqrt{3})^{2}} \\ {x^{2}=4 \cdot 3} \\ {x^{2}=12}\end{array}\)
Lastly, subtract 12 from both sides and present the equation in standard form.
Answer:
\(x^{2}-12=0\)
Solve:
\(9x^{2}-8=0\).
- Answer
-
\(x=-\frac{2 \sqrt{2}}{3}\) or \(x=\frac{2 \sqrt{2}}{3}\)
Consider solving the following equation:
\((x+2)^{2}=25\)
To solve this equation by factoring, first square x+2 and then put it in standard form, equal to zero, by subtracting 25 from both sides.
Factor and then apply the zero-product property.
\(\begin{array}{c}{x^{2}+4 x-21=0} \\ {(x+7)(x-3)=0}\end{array}\)
\(\begin{array}{rr}{x+7=0} & {\text { or } \quad x-3=0} \\ {x=-7} & {x=3}\end{array}\)
The two solutions are -7 and 3.
When an equation is in this form, we can obtain the solutions in fewer steps by extracting the roots.
Solve:
\((x=2)^{2}=25\).
Solution
Solve by extracting the roots.
\(\begin{array}{rlrr}{(x+2)^{2}} & {=25} & {\color{Cerulean}{ Apply\: the\:square \:root \:property.}} \\ {x+2} & {=\pm \sqrt{25}} & {\color{Cerulean}{ Simplify. }} \\ {x+2}& {=\pm5} \\ {x}&{=-2\pm5}\end{array}\)
At this point, separate the “plus or minus” into two equations and simplify each individually.
\(\begin{array}{ll}{x=-2-5} & {\text { or } x=-2+5} \\ {x=-7} & {\quad\:\: x=3}\end{array}\)
Answer:
The solutions are -7 and 3.
In addition to fewer steps, this method allows us to solve equations that do not factor.
Solve:
\((3 x+3)^{2}-27=0\)
Solution
Begin by isolating the square.
Next, extract the roots and simplify.
\(\begin{aligned}(3 x+3)^{2} &=27 \\ 3 x+3 &=\pm \sqrt{27} \\ 3 x+3 &=\pm \sqrt{9 \cdot 3} \\ 3 x+3 &=\pm 3 \sqrt{3} \end{aligned}\)
Solve for x.
Answer:
The solutions are \(-1 - \sqrt{3}\) and \(-1 + \sqrt{3}\)
Example \(\PageIndex{8}\)
Solve:
\(9(2 x-1)^{2}-8=0\)
Solution:
Begin by isolating the square factor.
Apply the square root property and solve.
Answer:
The solutions are \(\frac{3 - 2 \sqrt{2}}{6}\) and \(\frac{3 + 2 \sqrt{2}}{6}\)
Solve:
\(3(x-5)^{2}-2=0\)
- Answer
-
\(15\pm 6\sqrt{3}\)
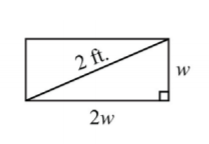
The length of a rectangle is twice its width. If the diagonal measures 2 feet, then find the dimensions of the rectangle.
.png?revision=1)
Solution
Let w represent the width.
Let 2w represent the length.
The diagonal of any rectangle forms two right triangles. Thus the Pythagorean theorem applies. The sum of the squares of the legs of a right triangle is equal to the square of the hypotenuse:
\(\begin{array}{l}{(\operatorname{leg})^{2}+(\operatorname{leg})^{2}=\text { hypotenuse }^{2}} \\ {(\color{OliveGreen}{2 w}\color{black}{)}^{2}+(\color{OliveGreen}{w}\color{black}{)}^{2}=(\color{OliveGreen}{2}\color{black}{)}^{2}}\end{array}\)
Solve.
\(\begin{aligned}(2 w)^{2}+(w)^{2} &=(2)^{2} \\ 4 w^{2}+w^{2} &=4 \\ 5 w^{2} &=4 \quad\quad\quad\color{Cerulean}{Isolate\:w^{2}.} \\\frac{5w^{2}}{\color{Cerulean}{5}}&\color{black}{=}\frac{4}{\color{Cerulean}{5}}\\ w^{2}&=\frac{4}{5}\quad\:\:\quad\color{Cerulean}{Extract\:the\:roots.} \\ w&=\pm\sqrt{\frac{4}{5}}\\w&=\pm\frac{2}{\sqrt{5}} \end{aligned}\)
Here we obtain two solutions, \(w=−\frac{2}{\sqrt{5}}\) and \(w=\frac{2}{\sqrt{5}}\). Since the problem asked for a length of a rectangle, we disregard the negative answer. Furthermore, we will rationalize the denominator and present our solutions without any radicals in the denominator.
\(\begin{aligned} w &=\frac{2}{\sqrt{5}} \quad\quad\quad\quad\color{Cerulean}{Rationalize\:the\:denominator.} \\ &=\frac{2}{\sqrt{5}} \cdot \color{Cerulean}{\frac{\sqrt{5}}{\sqrt{5}}} \\ &=\frac{2 \sqrt{5}}{\sqrt{25}} \\ &=\frac{2 \sqrt{5}}{5} \end{aligned}\)
Back substitute to find the length.
\(\begin{aligned} l &=2 w \\ &=2\color{black}{\left(\color{OliveGreen}{\frac{2 \sqrt{5}}{5}}\right)} \\ &=\frac{4 \sqrt{5}}{5} \end{aligned}\)
Answer:
The length of the rectangle is \(\frac{4 \sqrt{5}}{5}\) feet and the width is \(\frac{2 \sqrt{5}}{5}\) feet.
Key Takeaways
- Solve equations of the form \(ax^{2}+c=0\) by extracting the roots.
- Extracting roots involves isolating the square and then applying the square root property. After applying the square root property, you have two linear equations that each can be solved. Be sure to simplify all radical expressions and rationalize the denominator if necessary.
Solve by factoring and then solve by extracting roots. Check answers.
- \(x^{2}-36=0\)
- \(x^{2}-81=0\)
- \(4y^{2}−9=0\)
- \(9y^{2}−25=0\)
- \((x−2)^{2}−1=0\)
- \((x+1)^{2}−4=0\)
- \(4(y−2)^{2}−9=0\)
- \(9(y+1)^{2}−4=0\)
- \(−3(t−1)^{2}+12=0\)
- \(−2(t+1)^{2}+8=0\)
- \((x−5)^{2}−25=0\)
- \((x+2)^{2}−4=0\)
- Answer
-
1. \(-6, 6\)
3. \(-\frac{3}{2} , \frac{3}{2}\)
5. \(1, 3\)
7. \(\frac{1}{2}, \frac{7}{2}\)
9. \(-1, 3\)
11. \(0, 10\)
Solve by extracting the roots.
- \(x^{2}=16\)
- \(x^{2}=1\)
- \(y^{2}=9\)
- \(y^{2}=64\)
- \(x^{2}=14\)
- \(x^{2}=19\)
- \(y^{2}=0.25\)
- \(y^{2}=0.04\)
- \(x^{2}=12\)
- \(x^{2}=18\)
- \(16x^{2}=9\)
- \(4x^{2}=25\)
- \(2t^{2} = 1\)
- \(3t^{2} = 2\)
- \(x^{2} −100 = 0\)
- \(x^{2} −121 = 0\)
- \(y^{2} + 4 = 0\)
- \(y^{2} + 1 = 0\)
- \(x^{2} −49 = 0\)
- \(x^{2} −925 = 0\)
- \(y^{2} −0.09 = 0\)
- \(y^{2} −0.81 = 0\)
- \(x^{2} − 7 = 0\)
- \(x^{2} − 2 = 0\)
- \(x^{2} − 8 = 0\)
- \(t^{2} −18 = 0\)
- \(x^{2} + 8 = 0\)
- \(x^{2} +125 = 0\)
- \(16x^{2} −27 = 0\)
- \(9x^{2} − 8 = 0\)
- \(2y^{2} − 3 = 0\)
- \(5y^{2} − 2 = 0\)
- \(3x^{2} − 1 = 0\)
- \(6x^{2} − 3 = 0\)
- \((x + 7 )^{2} − 4 = 0\)
- \((x + 9 )^{2} −36 = 0\)
- \(( 2y − 3 )^{2} −81 = 0 \)
- \(( 2y + 1 )^{2} −25 = 0\)
- \((x − 5 )^{2} −20 = 0\)
- \((x + 1 )^{2} −28 = 0\)
- \(( 3t + 2 )^{2} − 6 = 0\)
- \((3t−5)^{2}−10=0\)
- \(4(y+2)^{2}−3=0\)
- \(9(y−7)^{2}−5=0\)
- \(4(3x+1)^{2}−27=0\)
- \(9(2x−3)^{2}−8=0\)
- \(2(3x−1)^{2}+3=0\)
- \(5(2x−1)^{2}−3=0\)
- \(3(y−23)^{2}−32=0\)
- \(2(3y−13)^{2}−52=0\)
- Answer
-
1. ±4
3. ±3
5. ±\(\frac{1}{2}\)
7. ±0.5
9. ±\(2\sqrt{3}\)
11. ±\(\frac{3}{4}\)
13. ±\(\sqrt{\frac{1}{2}}\)
15. ±10
17. No real solution
19. ±\(\frac{2}{3}\)
21. ±0.3
23. ±\(\sqrt{7}\)
25. ±\(2\sqrt{2}\)
27. No real solution
29. ±\(\frac{3 \sqrt{3}}{4}\)
31. ±\(6\sqrt{2}\)
33. ±\(3\sqrt{3}\)
35. \(−9, −5\)
37. \(−3, 6\)
39. \(5\)±\(2\sqrt{5}\)
41. ±\(\frac{\sqrt{6}-2}{3}\)
43. ±\(\frac{\sqrt{3}}{2}-2\)
45. ±\(\frac{3 \sqrt{3}-2}{6}\)
47. No real solution
49. ±\(\frac{4 \sqrt{6}}{3}+23\)
Find a quadratic equation in standard form with the following solutions.
- ±7
- ±13
- ±\(\sqrt{7}\)
- ±\(\sqrt{3}\)
- ±\(3\sqrt{5}\)
- ±\(5\sqrt{2}\)
- \(1\)±\(\sqrt{2}\)
- \(2\)±\(\sqrt{3}\)
- Answer
-
1. \(x^{2}−49=0\)
3. \(x^{2}−7=0\)
5. \(x^{2}−45=0\)
7. \(x^{2}−2x−1=0\)
Solve and round off the solutions to the nearest hundredth.
- \(9x(x+2)=18x+1\)
- \(x^{2}=10(x^{2}−2)−5\)
- \((x+3)(x−7)=11−4x\)
- \((x−4)(x−3)=66−7x\)
- \((x−2)^{2}=67−4x\)
- \((x+3)^{2}=6x+59\)
- \((2x+1)(x+3)−(x+7)=(x+3)^{2}\)
- \((3x−1)(x+4)=2x(x+6)−(x−3)\)
- Answer
-
1. ±0.33
3. ±5.66
5. ±7.94
7. ±3.61
Set up an algebraic equation and use it to solve the following.
- If 9 is subtracted from 4 times the square of a number, then the result is 3. Find the number.
- If 20 is subtracted from the square of a number, then the result is 4. Find the number.
- If 1 is added to 3 times the square of a number, then the result is 2. Find the number.
- If 3 is added to 2 times the square of a number, then the result is 12. Find the number.
- If a square has an area of 8 square centimeters, then find the length of each side.
- If a circle has an area of 32\(\pi\) square centimeters, then find the length of the radius.
- The volume of a right circular cone is 36\(\pi\) cubic centimeters when the height is 6 centimeters. Find the radius of the cone. (The volume of a right circular cone is given by \(V=13\pi r^{2}h\).)
- The surface area of a sphere is 75\(\pi\) square centimeters. Find the radius of the sphere. (The surface area of a sphere is given by SA=\(4\pi r^{2}\).)
- The length of a rectangle is 6 times its width. If the area is 96 square inches, then find the dimensions of the rectangle.
- The base of a triangle is twice its height. If the area is 16 square centimeters, then find the length of its base.
- A square has an area of 36 square units. By what equal amount will the sides have to be increased to create a square with double the given area?
- A circle has an area of 25\(\pi\) square units. By what amount will the radius have to be increased to create a circle with double the given area?
- If the sides of a square measure 1 unit, then find the length of the diagonal.
- If the sides of a square measure 2 units, then find the length of the diagonal.
- The diagonal of a square measures 5 inches. Find the length of each side.
- The diagonal of a square measures 3 inches. Find the length of each side.
- The length of a rectangle is twice its width. If the diagonal measures 10 feet, then find the dimensions of the rectangle.
- The length of a rectangle is twice its width. If the diagonal measures 8 feet, then find the dimensions of the rectangle.
- The length of a rectangle is 3 times its width. If the diagonal measures 5 meters, then find the dimensions of the rectangle.
- The length of a rectangle is 3 times its width. If the diagonal measures 2 feet, then find the dimensions of the rectangle.
- The height in feet of an object dropped from a 9-foot ladder is given by h(t)\(=−16t^{2}+9\), where t represents the time in seconds after the object has been dropped. How long does it take the object to hit the ground? (Hint: The height is 0 when the object hits the ground.)
- The height in feet of an object dropped from a 20-foot platform is given by h(t)\(=−16t^{2}+20\), where t represents the time in seconds after the object has been dropped. How long does it take the object to hit the ground?
- The height in feet of an object dropped from the top of a 144-foot building is given by h(t)\(=−16t^{2}+144\), where t is measured in seconds.
- How long will it take to reach half of the distance to the ground, 72 feet?
- How long will it take to travel the rest of the distance to the ground? Round off to the nearest hundredth of a second.
- The height in feet of an object dropped from an airplane at 1,600 feet is given by h(t)\(=−16t^{2}+1,600\), where t is in seconds.
- How long will it take to reach half of the distance to the ground?
- How long will it take to travel the rest of the distance to the ground? Round off to the nearest hundredth of a second.
- Create an equation of your own that can be solved by extracting the root. Share it, along with the solution, on the discussion board.
- Explain why the technique of extracting roots greatly expands our ability to solve quadratic equations.
- Explain in your own words how to solve by extracting the roots. 106. Derive a formula for the diagonal of a square in terms of its sides.
- Answer
-
1. \(−\sqrt{3}\) or \(\sqrt{3}\)
3. \(−3\sqrt{3}\) or \(3\sqrt{3}\)
5. \(2\sqrt{2}\) centimeters
7. \(3\sqrt{2}\) centimeters
9. Length: 24 inches; width: 4 inches
11. \(−6+6\sqrt{2}\approx 2.49\) units
13. \(\sqrt{2}\) units
15. \(52\sqrt{2}\) inches
17. Length: \(4\sqrt{5}\) feet; width: \(2\sqrt{5}\) feet
19. Length: \(310−−\sqrt{2}\) meters; width: \(10−−\sqrt{2}\) meters
21. \(\frac{3}{4}\) second
23. a. 2.12 seconds b. 0.88 second
25. Answers may vary


