4.3: Graph with Intercepts

Last updated
Save as PDF

Page ID: 15145

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

By the end of this section, you will be able to:

Identify the x- and y- intercepts on a graph
Find the x- and y- intercepts from an equation of a line
Graph a line using the intercepts

Note

Before you get started, take this readiness quiz.

Solve: $3\cdot 0+4y=−2$.
If you missed this problem, review Exercise 2.2.13.

Identify the x- and y- Intercepts on a Graph

Every linear equation can be represented by a unique line that shows all the solutions of the equation. We have seen that when graphing a line by plotting points, you can use any three solutions to graph. This means that two people graphing the line might use different sets of three points.

At first glance, their two lines might not appear to be the same, since they would have different points labeled. But if all the work was done correctly, the lines should be exactly the same. One way to recognize that they are indeed the same line is to look at where the line crosses the x- axis and the y- axis. These points are called the intercepts of the line.

INTERCEPTS OF A LINE

The points where a line crosses the x- axis and the y- axis are called the intercepts of a line.

Let’s look at the graphs of the lines in Figure $\PageIndex{1}$.

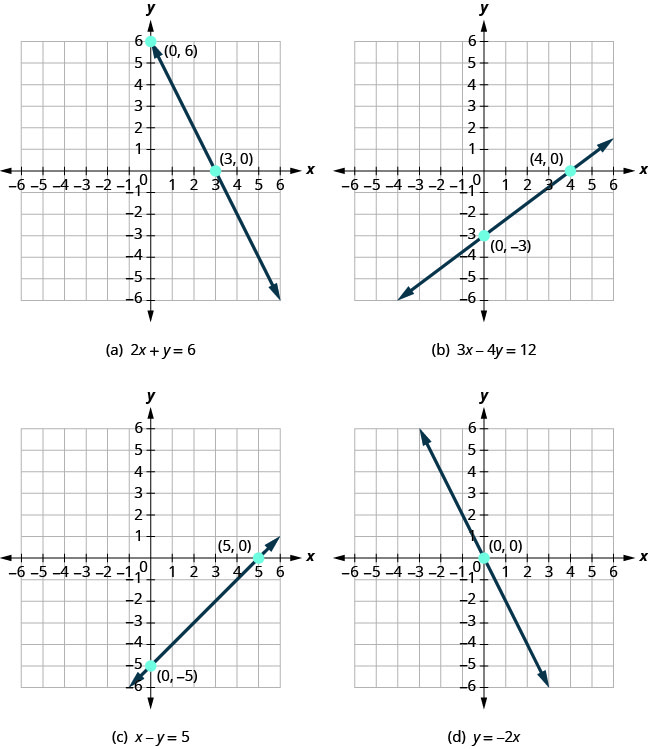
Four figures, each showing a different straight line on the x y- coordinate plane. The x- axis of the planes runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. Figure a shows a straight line crossing the x- axis at the point (3, 0) and crossing the y- axis at the point (0, 6). The graph is labeled with the equation 2x plus y equals 6. Figure b shows a straight line crossing the x- axis at the point (4, 0) and crossing the y- axis at the point (0, negative 3). The graph is labeled with the equation 3x minus 4y equals 12. Figure c shows a straight line crossing the x- axis at the point (5, 0) and crossing the y- axis at the point (0, negative 5). The graph is labeled with the equation x minus y equals 5. Figure d shows a straight line crossing the x- axis and y- axis at the point (0, 0). The graph is labeled with the equation y equals negative 2x. — Figure $\PageIndex{1}$: Examples of graphs crossing the x-negative axis.

First, notice where each of these lines crosses the x axis. See Figure $\PageIndex{1}$.

Table $\PageIndex{1}$
Figure	The line crosses the x-axis at:	Ordered pair of this point
Figure (a)	3	(3,0)
Figure (b)	4	(4,0)
Figure (c)	5	(5,0)
Figure (d)	0	(0,0)

Do you see a pattern?

For each row, the y- coordinate of the point where the line crosses the x- axis is zero. The point where the line crosses the x- axis has the form (a,0) and is called the x- intercept of a line. The x- intercept occurs when y is zero. Now, let’s look at the points where these lines cross the y- axis. See Table $\PageIndex{2}$.

Table $\PageIndex{2}$
Figure	The line crosses the x-axis at:	Ordered pair of this point
Figure (a)	6	(0,6)
Figure (b)	−3	(0,−3)
Figure (c)	−5	(0,5)
Figure (d)	0	(0,0)

What is the pattern here?

In each row, the x- coordinate of the point where the line crosses the y- axis is zero. The point where the line crosses the y- axis has the form (0,b) and is called the y- intercept of the line. The y- intercept occurs when x is zero.

X- INTERCEPT AND Y- INTERCEPT OF A LINE

The x- intercept is the point (a,0) where the line crosses the x- axis.

The y- intercept is the point (0,b) where the line crosses the y- axis.

Example $\PageIndex{1}$

Find the x- and y- intercepts on each graph.

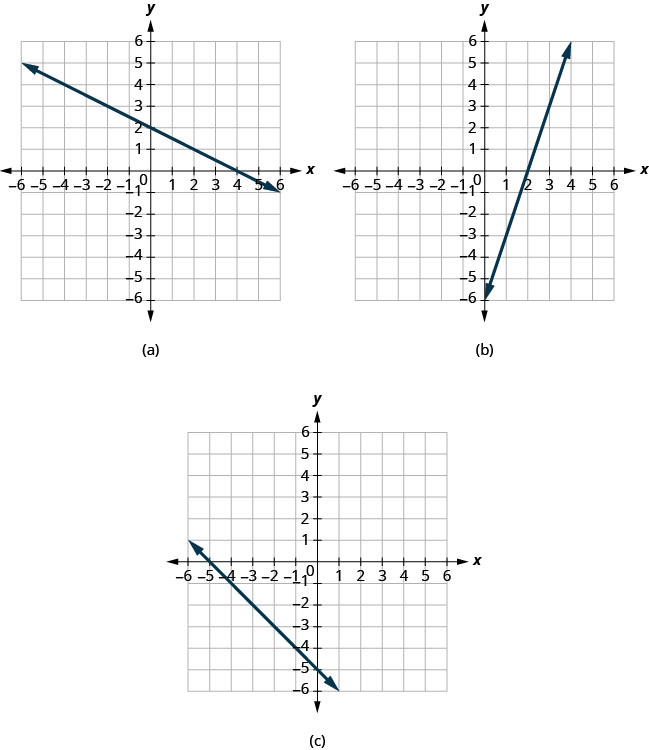
Three figures, each showing a different straight line on the x y- coordinate plane. The x- axis of the planes runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. Figure a shows a straight line going through the points (negative 6, 5), (negative 4, 4), (negative 2, 3), (0, 2), (2, 1), (4, 0), and (6, negative 1). Figure b shows a straight line going through the points (0, negative 6), (1, negative 3), (2, 0), (3, 3), and (4, 6). Figure c shows a straight line going through the points (negative 6, 1), (negative 5, 0), (negative 4, negative 1), (negative 3, negative 2), (negative 2, negative 3), (negative 1, negative 4), (0, negative 5), and (1, negative 6). — Figure $\PageIndex{3}$

Solution

(a) The graph crosses the x- axis at the point (4,0). The x- intercept is (4,0).
The graph crosses the y- axis at the point (0,2). The y- intercept is (0,2).

(b) The graph crosses the x- axis at the point (2,0). The x- intercept is (2,0)
The graph crosses the y- axis at the point (0,−6). The y- intercept is (0,−6).

(c) The graph crosses the x- axis at the point (−5,0). The x- intercept is (−5,0).
The graph crosses the y- axis at the point (0,−5). The y- intercept is (0,−5).

Try It $\PageIndex{2}$

Find the x- and y- intercepts on the graph.

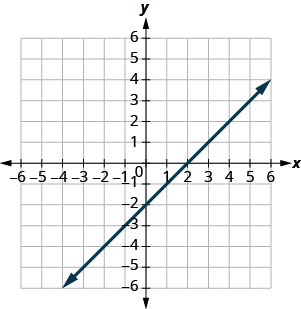
$A figure showing a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 8, negative 10), (negative 6, negative 8), (negative 4, negative 6), (negative 2, negative 4), (0, negative 2), (2, 0), (4, 2), (6, 4), (8, 6), and (10, 8).$

Answer: x- intercept: (2,0); y- intercept: (0,−2)

Try It $\PageIndex{3}$

Find the x- and y- intercepts on the graph.

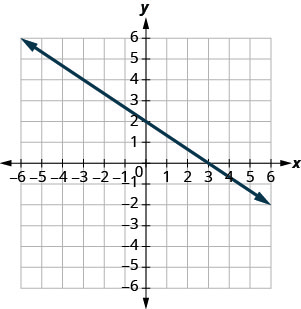
$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 9, 8), (negative 6, 6), (negative 3, 4), (0, 2), (3, 0), (6, negative 2), and (9, negative 4).$

Answer: x- intercept: (3,0), y- intercept: (0,2)

Find the x- and y- Intercepts from an Equation of a Line

Recognizing that the x- intercept occurs when y is zero and that the y- intercept occurs when x is zero, gives us a method to find the intercepts of a line from its equation. To find the x- intercept, let y=0 and solve for x. To find the y- intercept, let x=0 and solve for y.

X- AND Y- INTERCEPTS FROM THE EQUATION OF A LINE

Use the equation of the line. To find:

the x- intercept of the line, let y=0 and solve for x.
the y- intercept of the line, let x=0 and solve for y.

Example $\PageIndex{4}$

Find the intercepts of 2x+y=6.

Solution

We will let y=0 to find the x- intercept, and let x=0 to find the y- intercept. We will fill in the table, which reminds us of what we need to find.

$The figure shows a table with four rows and two columns. The first row is a title row and it labels the table with the equation 2 x plus y equals 6. The second row is a header row and it labels each column. The first column header is “x” and the second is "y". The third row is labeled “x- intercept” and has the first column blank and a 0 in the second column. The fourth row is labeled “y- intercept” and has a 0 in the first column with the second column blank.$

To find the x- intercept, let y=0.

Table $\PageIndex{3}$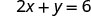
	$.$
Let y = 0.	$.$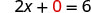
Simplify.	$.$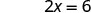
	$.$
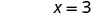
The x-intercept is	(3, 0)
To find the y-intercept, let x = 0.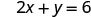
	$.$
Let x = 0.	$.$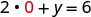
Simplify.	$.$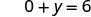
	$.$
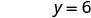
The y-intercept is	(0, 6)

The intercepts are the points (3,0) and (0,6) as shown in Table $\PageIndex{4}$.

Table $\PageIndex{4}$
2x+y=6
x	y
3	0
0	6

Try It $\PageIndex{5}$

Find the intercepts of 3x+y=12.

Answer: x- intercept: (4,0), y- intercept: (0,12)

Try It $\PageIndex{6}$

Find the intercepts of x+4y=8.

Answer: x- intercept: (8,0), y- intercept: (0,2)

Example $\PageIndex{7}$

Find the intercepts of 4x–3y=12.

Solution

To find the x-intercept, let y = 0.
	$.$
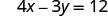Let y = 0.	$.$
Simplify.	$.$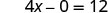
	$.$
	$.$
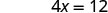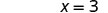The x-intercept is	(3, 0)
To find the y-intercept, let x = 0.
	$.$
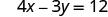Let x = 0.	$.$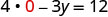
Simplify.	$.$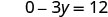
	$.$
	$.$
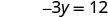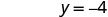The y-intercept is	(0, −4)

Table $\PageIndex{5}$

The intercepts are the points (3, 0) and (0, −4) as shown in the following table.

Table $\PageIndex{6}$
4x−3y=12
x	y
3	0
0	−4

Try It $\PageIndex{8}$

Find the intercepts of 3x–4y=12.

Answer: x- intercept: (4,0), y- intercept: (0,−3)

Try It $\PageIndex{9}$

Find the intercepts of 2x–4y=8.

Answer: x- intercept: (4,0), y- intercept: (0,−2)

Graph a Line Using the Intercepts

To graph a linear equation by plotting points, you need to find three points whose coordinates are solutions to the equation. You can use the x- and y- intercepts as two of your three points. Find the intercepts, and then find a third point to ensure accuracy. Make sure the points line up—then draw the line. This method is often the quickest way to graph a line.

Example $\PageIndex{10}$: How to Graph a Line Using Intercepts

Graph –x+2y=6 using the intercepts.

Solution

$The figure shows a table with the general procedure for graphing a line using the intercepts along with a specific example using the equation negative x plus 2y equals 6. Step 1 of the general procedure is “Find the x and y- intercepts of the line. Let y equals 0 and solve for x. Let x equals 0 and solve for y”. Step 1 for the example is a series of statements and equations: “Find the x- intercept. Let y equals 0”, negative x plus 2y equals 6, negative x plus 2(0) equals 6 (where the 0 is red), negative x equals 6, x equals negative 6, “The x- intercept is (negative 6, 0)”, “Find the y- intercept. Let x equals 0”, negative x plus 2y equals 6, negative 0 plus 2y equals 6 (where the 0 is red), 2y equals 6, y equals 3, and “The y- intercept is (0, 3)”.$ $Step 2 of the general procedure is “Find another solution to the equation.” Step 2 for the example is a series of statements and equations: “We’ll use x equals 2”, “Let x equals 2”, negative x plus 2y equals 6, negative 2 plus 2y equals 6 (where the first 2 is red), 2y equals 8, y equals 4, and “A third point is (2, 4)”. Step 3 of the general procedure is “Plot the three points. 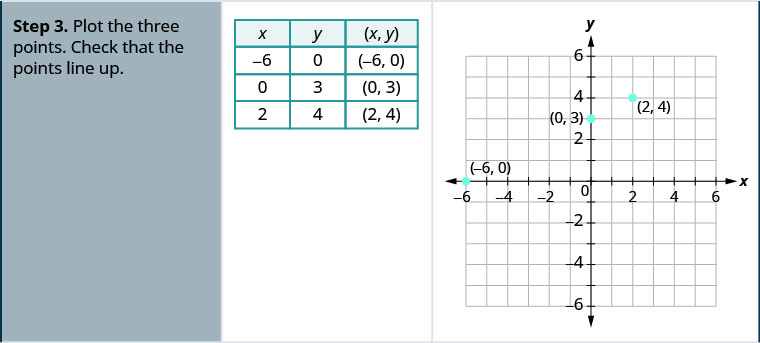Check that the points line up.”$ $Step 3 for the example is a table and a graph. The table has four rows and three columns. The first row is a header row and it labels each column. The first column header is “x”, the second is "y", and the third is “(x,y)”. Under the first column are the numbers negative 6, 0 and 2. Under the second column are the numbers 0, 3, and 4. Under the third column are the ordered pairs (negative 6, 0), (0, 3), and (2, 4). The graph has three points on the x- y coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. 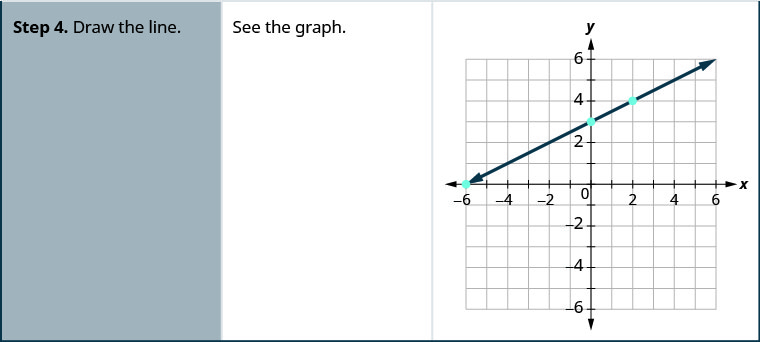Three points are marked at (negative 6, 0), (0, 3), and (2, 4).$ $Step 4 of the general procedure is “Draw the line.” For the specific example, there is the statement “See the graph” and a graph of a straight line going through three points on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. Three points are marked at (negative 6, 0), (0, 3), and (2, 4). The straight line is drawn through the points (negative 6, 0), (negative 4, 1), (negative 2, 2), (0, 3), (2, 4), (4, 5), and (6, 6).$

Try It $\PageIndex{11}$

Graph x–2y=4 using the intercepts.

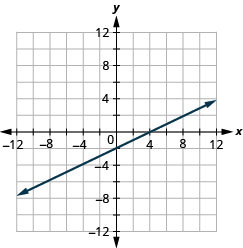
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 10, negative 7), (negative 8, negative 6), (negative 6, negative 5), (negative 4, negative 4), (negative 2, negative 3), (0, negative 2), (2, negative 1), (4, 0), (6, 1), (8, 2), and (10, 3).$

Try It $\PageIndex{12}$

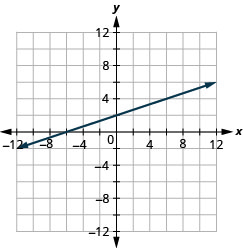
Graph –x+3y=6 using the intercepts.

Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 12, negative 2), (negative 9, negative 1), (negative 6, 0), (negative 3, 1), (0, 2), (3, 3), (6, 4), (9, 5), and (12, 6).$

The steps to graph a linear equation using the intercepts are summarized below.

GRAPH A LINEAR EQUATION USING THE INTERCEPTS.

Find the x- and y- intercepts of the line.
- Let y=0 and solve for x
- Let x=0 and solve for y.
Find a third solution to the equation.
Plot the three points and check that they line up.
Draw the line.

Example $\PageIndex{13}$

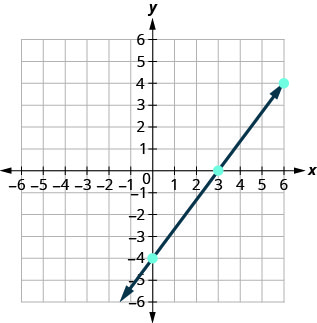
Graph 4x–3y=12 using the intercepts.

Solution

Find the intercepts and a third point.

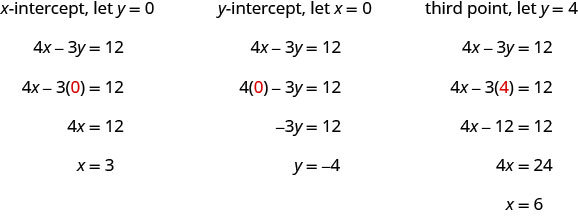
$The figure shows a series of statements and equations: “Find the x- intercept. Let y equals 0”, 4x minus 3y equals 12, 4x minus 3(0) equals 12 (where the 0 is red), 4x equals 12, x equals 3, “Find the y- intercept. Let x equals 0”, 4x minus 3y equals 12, 4(0) minus 3y equals 12 (where the 0 is red), negative 3y equals 12, y equals negative 4, “third point, let y equals 4”, 4x minus 3y equals 12, 4x minus 3(4) equals 12 (where the second 4 is red), 4x minus 12 equals 12, 4x equals 24, and x equals 6.$

We list the points in Table $\PageIndex{7}$ and show the graph below.

4x−3y=12
x	y	(x,y)
3	0	(3,0)
0	−4	(0,−4)
6	4	(6,4)

Table $\PageIndex{7}$

$The figure shows the graph of a straight line going through three points on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. Three points are marked at (0, negative 4), (3, 0), and (6, 4). The straight line is drawn through the points (0, negative 4), (3, 0), and (6, 4).$

Try It $\PageIndex{14}$

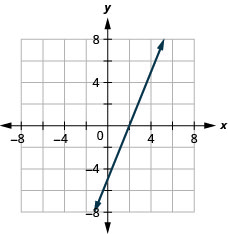
Graph 5x–2y=10 using the intercepts.

Answer: $The figure shows the graph of a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. The straight line goes through the points (0, negative 5), (2, 0), and (4, 5).$

Try It $\PageIndex{15}$

Graph 3x–4y=12 using the intercepts.

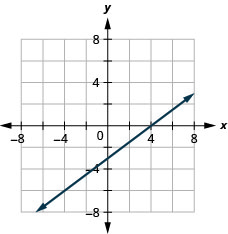
Answer: $The figure shows the graph of a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. The straight line goes through the points (negative 4, negative 6), (0, negative 3), and (4, 0).$

Example $\PageIndex{16}$

Graph y=5x using the intercepts.

Solution

$The figure shows two sets of statements and equations to find the intercepts from an equation. The first set of statements and equations is “x- intercept”, “let y equals 0”, y equals 5x, 0 equals 5x (where the 0 is red), 0 equals x, (0, 0). The second set of statements and equations is “y- intercept”, “let x equals 0”, y equals 5x, y equals 5(0) (where the 0 is red), y equals 0, (0, 0).$

This line has only one intercept. It is the point (0,0).

To ensure accuracy we need to plot three points. Since the x- and y- intercepts are the same point, we need two more points to graph the line.

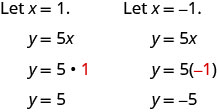
$The figure shows two sets of statements and equations to find two points from an equation. The first set of statements and equations is “Let x equals 1”, y equals 5x, y equals 5(1) (where the 1 is red), y equals 5. The second set of statements and equations is “Let x equals negative 1”, y equals 5x, y equals 5(negative 1) (where the negative 1 is red), y equals negative 5.$

See Table $\PageIndex{8}$.

y=5x
x	y	(x,y)
0	0	(0,0)
1	5	(1,5)
−1	−5	(−1,−5)

Table $\PageIndex{8}$

Plot the three points, check that they line up, and draw the line.

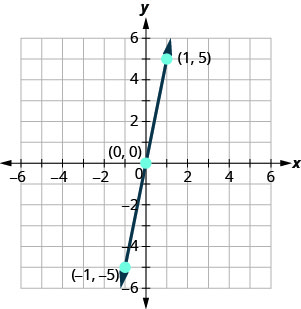
$The figure shows the graph of a straight line going through three points on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. Three points are marked and labeled with their coordinates at (negative 1, negative 5), (0, 0), and (1, 5). The straight line is drawn through the points (negative 1, negative 5), (0, 0), and (1, 5).$

Try It $\PageIndex{17}$

Graph y=4x using the intercepts.

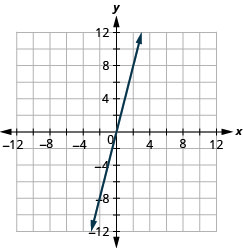
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 4, negative 12), (negative 3, negative 9), (negative 2, negative 6), (negative 1, negative 3), (0, 0), (1, 3), (2, 6), (3, 9), and (4, 12).$

Try It $\PageIndex{18}$

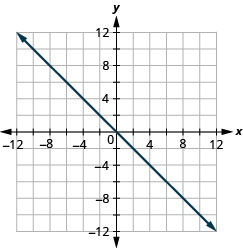
Graph y=−x the intercepts.

Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 10, 10), (negative 9, 9), (negative 8, 8), (negative 7, 7), (negative 6, 6), (negative 5, 5), (negative 4, 4), (negative 3, 3), (negative 2, 2), (negative 1, 1), (0, 0), (1, negative 1), (2, negative 2), (3, negative 3), (4, negative 4), (5, negative 5), (6, negative 6), (7, negative 7), (8, negative 8), (9, negative 9), and (10, negative 10).$

Key Concepts

Find the x- and y- Intercepts from the Equation of a Line
- Use the equation of the line to find the x- intercept of the line, let y=0 and solve for x.
- Use the equation of the line to find the y- intercept of the line, let x=0 and solve for y.
Graph a Linear Equation using the Intercepts
1. Find the x- and y- intercepts of the line.
  Let y=0 and solve for x.
  Let x=0 and solve for y.
2. Find a third solution to the equation.
3. Plot the three points and then check that they line up.
4. Draw the line.
Strategy for Choosing the Most Convenient Method to Graph a Line:
- Consider the form of the equation.
- If it only has one variable, it is a vertical or horizontal line.
  x=a is a vertical line passing through the x- axis at a
  y=b is a horizontal line passing through the y- axis at b.
- If y is isolated on one side of the equation, graph by plotting points.
- Choose any three values for x and then solve for the corresponding y- values.
- If the equation is of the form ax+by=c, find the intercepts. Find the x- and y- intercepts and then a third point.

Glossary

intercepts of a line: The points where a line crosses the x- axis and the y- axis are called the intercepts of the line.

x- intercept: The point (a,0) where the line crosses the x- axis; the x- intercept occurs when y is zero.

y-intercept: The point (0,b) where the line crosses the y- axis; the y- intercept occurs when x is zero.

Search

Text Color

Text Size

Margin Size

Font Type

INTERCEPTS OF A LINE

X- INTERCEPT AND Y- INTERCEPT OF A LINE

Example \(\PageIndex{1}\)

Try It \(\PageIndex{2}\)

Try It \(\PageIndex{3}\)

X- AND Y- INTERCEPTS FROM THE EQUATION OF A LINE

Example \(\PageIndex{4}\)

Try It \(\PageIndex{5}\)

Try It \(\PageIndex{6}\)

Example \(\PageIndex{7}\)

Try It \(\PageIndex{8}\)

Try It \(\PageIndex{9}\)

Example \(\PageIndex{10}\): How to Graph a Line Using Intercepts

Try It \(\PageIndex{11}\)

Try It \(\PageIndex{12}\)

GRAPH A LINEAR EQUATION USING THE INTERCEPTS.

Example \(\PageIndex{13}\)

Try It \(\PageIndex{14}\)

Try It \(\PageIndex{15}\)

Example \(\PageIndex{16}\)

Try It \(\PageIndex{17}\)

Try It \(\PageIndex{18}\)