Chapter 5 Review Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Chapter 5 Review Exercises
Solve Systems of Equations by Graphing
Determine Whether an Ordered Pair is a Solution of a System of Equations.
In the following exercises, determine if the following points are solutions to the given system of equations.
{x+3y=−92x−4y=12
- (−3,−2)
- (0,−3)
- Answer
-
- no
- yes
{x+y=8y=x−4
- (6,2)
- (9,−1)
Solve a System of Linear Equations by Graphing
In the following exercises, solve the following systems of equations by graphing.
{3x+y=6x+3y=−6
- Answer
-
(3,−3)
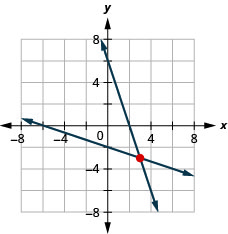
{y=x−2y=−2x−2
{2x−y=6y=4
- Answer
-
(5,4)
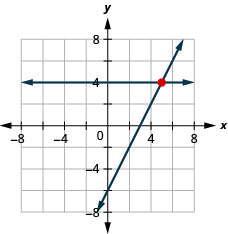
{x+4y=−1x=3
{2x−y=54x−2y=10
- Answer
-
coincident lines
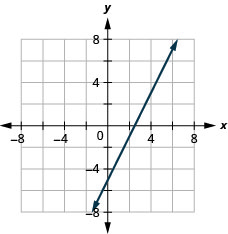
{−x+2y=4y=12x−3
Determine the Number of Solutions of a Linear System
In the following exercises, without graphing determine the number of solutions and then classify the system of equations.
{y=25x+2−2x+5y=10
- Answer
-
infinitely many solutions, consistent system, dependent equations
{3x+2y=6y=−3x+4
{5x−4y=0y=54x−5
- Answer
-
no solutions, inconsistent system, independent equations
{y=−34x+16x+8y=8
Solve Applications of Systems of Equations by Graphing
LaVelle is making a pitcher of caffe mocha. For each ounce of chocolate syrup, she uses five ounces of coffee. How many ounces of chocolate syrup and how many ounces of coffee does she need to make 48 ounces of caffe mocha?
- Answer
-
LaVelle needs 8 ounces of chocolate syrup and 40 ounces of coffee.
Eli is making a party mix that contains pretzels and chex. For each cup of pretzels, he uses three cups of chex. How many cups of pretzels and how many cups of chex does he need to make 12 cups of party mix?
Solve Systems of Equations by Substitution
Solve a System of Equations by Substitution
In the following exercises, solve the systems of equations by substitution.
{3x−y=−5y=2x+4
- Answer
-
(−1,2)
{3x−2y=2y=12x+3
{x−y=02x+5y=−14
- Answer
-
(−2,−2)
{y=−2x+7y=23x−1
{y=−5x5x+y=6
- Answer
-
no solution
{y=−13x+2x+3y=6
Solve Applications of Systems of Equations by Substitution
In the following exercises, translate to a system of equations and solve.
The sum of two number is 55. One number is 11 less than the other. Find the numbers.
- Answer
-
The numbers are 22 and 33.
The perimeter of a rectangle is 128. The length is 16 more than the width. Find the length and width.
The measure of one of the small angles of a right triangle is 2 less than 3 times the measure of the other small angle. Find the measure of both angles.
- Answer
-
The measures are 23 degrees and 67 degrees.
Gabriela works for an insurance company that pays her a salary of $32,000 plus a commission of $100 for each policy she sells. She is considering changing jobs to a company that would pay a salary of $40,000 plus a commission of $80 for each policy sold. How many policies would Gabriela need to sell to make the total pay the same?
Solve Systems of Equations by Elimination
Solve a System of Equations by Elimination In the following exercises, solve the systems of equations by elimination.
{x+y=12x−y=−10
- Answer
-
(1,11)
{4x+2y=2−4x−3y=−9
{3x−8y=20x+3y=1
- Answer
-
(4,−1)
{3x−2y=64x+3y=8
{9x+4y=25x+3y=5
- Answer
-
(−2,5)
{−x+3y=82x−6y=−20
Solve Applications of Systems of Equations by Elimination
In the following exercises, translate to a system of equations and solve.
The sum of two numbers is −90. Their difference is 16. Find the numbers.
- Answer
-
The numbers are −37 and −53.
Omar stops at a donut shop every day on his way to work. Last week he had 8 donuts and 5 cappuccinos, which gave him a total of 3,000 calories. This week he had 6 donuts and 3 cappuccinos, which was a total of 2,160 calories. How many calories are in one donut? How many calories are in one cappuccino?
Choose the Most Convenient Method to Solve a System of Linear Equations
In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.
{6x−5y=273x+10y=−24
- Answer
-
elimination
{y=3x−94x−5y=23
Solve Applications with Systems of Equations
Translate to a System of Equations
In the following exercises, translate to a system of equations. Do not solve the system.
The sum of two numbers is −32. One number is two less than twice the other. Find the numbers.
- Answer
-
{x+y=−32x=2y−2
Four times a number plus three times a second number is −9. Twice the first number plus the second number is three. Find the numbers.
Last month Jim and Debbie earned $7,200. Debbie earned $1,600 more than Jim earned. How much did they each earn?
- Answer
-
{j+d=7200d=j+1600
Henri has $24,000 invested in stocks and bonds. The amount in stocks is $6,000 more than three times the amount in bonds. How much is each investment?
Solve Direct Translation Applications
In the following exercises, translate to a system of equations and solve.
Pam is 3 years older than her sister, Jan. The sum of their ages is 99. Find their ages.
- Answer
-
Pam is 51 and Jan is 48.
Mollie wants to plant 200 bulbs in her garden. She wantsall irises and tulips. She wants to plant three times as many tulips as irises. How many irises and how many tulips should she plant?
Solve Geometry Applications
In the following exercises, translate to a system of equations and solve.
The difference of two supplementary angles is 58 degrees. Find the measures of the angles.
- Answer
-
The measures are 119 degrees and 61 degrees.
Two angles are complementary. The measure of the larger angle is five more than four times the measure of the smaller angle. Find the measures of both angles.
Becca is hanging a 28 foot floral garland on the two sides and top of a pergola to prepare for a wedding. The height is four feet less than the width. Find the height and width of the pergola.
Answer
-
The pergola is 8 feet high and 12 feet wide.
The perimeter of a city rectangular park is 1428 feet. The length is 78 feet more than twice the width. Find the length and width of the park.
Solve Uniform Motion Applications
In the following exercises, translate to a system of equations and solve.
Sheila and Lenore were driving to their grandmother’s house. Lenore left one hour after Sheila. Sheila drove at a rate of 45 mph, and Lenore drove at a rate of 60 mph. How long will it take for Lenore to catch up to Sheila?
- Answer
-
It will take Lenore 3 hours.
Bob left home, riding his bike at a rate of 10 miles per hour to go to the lake. Cheryl, his wife, left 45 minutes (34 hour) later, driving her car at a rate of 25 miles per hour. How long will it take Cheryl to catch up to Bob?
Marcus can drive his boat 36 miles down the river in three hours but takes four hours to return upstream. Find the rate of the boat in still water and the rate of the current.
- Answer
-
The rate of the boat is 10.5 mph. The rate of the current is 1.5 mph.
A passenger jet can fly 804 miles in 2 hours with a tailwind but only 776 miles in 2 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
Solve Mixture Applications with Systems of Equations
Solve Mixture Applications
In the following exercises, translate to a system of equations and solve.
Lynn paid a total of $2,780 for 261 tickets to the theater. Student tickets cost $10 and adult tickets cost $15. How many student tickets and how many adult tickets did Lynn buy?
- Answer
-
Lynn bought 227 student tickets and 34 adult tickets.
Priam has dimes and pennies in a cup holder in his car. The total value of the coins is $4.21. The number of dimes is three less than four times the number of pennies. How many dimes and how many pennies are in the cup?
Yumi wants to make 12 cups of party mix using candies and nuts. Her budget requires the party mix to cost her $1.29 per cup. The candies are $2.49 per cup and the nuts are $0.69 per cup. How many cups of candies and how many cups of nuts should she use?
- Answer
-
Yumi should use 4 cups of candies and 8 cups of nuts.
A scientist needs 70 liters of a 40% solution of alcohol. He has a 30% and a 60% solution available. How many liters of the 30% and how many liters of the 60% solutions should he mix to make the 40% solution?
Solve Interest Applications
In the following exercises, translate to a system of equations and solve.
Jack has $12,000 to invest and wants to earn 7.5% interest per year. He will put some of the money into a savings account that earns 4% per year and the rest into CD account that earns 9% per year. How much money should he put into each account?
- Answer
-
Jack should put $3600 into savings and $8400 into the CD.
When she graduates college, Linda will owe $43,000 in student loans. The interest rate on the federal loans is 4.5% and the rate on the private bank loans is 2%. The total interest she owes for one year was $1585. What is the amount of each loan?
Graphing Systems of Linear Inequalities
Determine Whether an Ordered Pair is a Solution of a System of Linear Inequalities
In the following exercises, determine whether each ordered pair is a solution to the system.
{4x+y>63x−y≤12
- (2,−1)
- (3,−2)
- Answer
-
- yes
- no
{y>13x+2x−14y≤10
- (6,5)
- (15,8)
Solve a System of Linear Inequalities by Graphing
In the following exercises, solve each system by graphing.
{y<3x+1y≥−x−2
- Answer
-
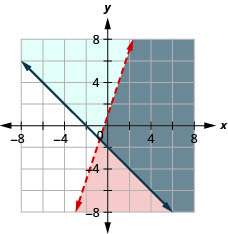
{x−y>−1y<13x−2
{2x−3y<63x+4y≥12
- Answer
-
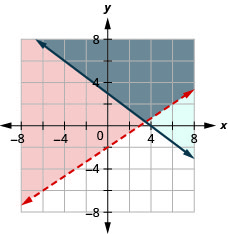
{y≤−34x+1x≥−5
{x+3y<5y≥−13x+6
- Answer
-
No solution
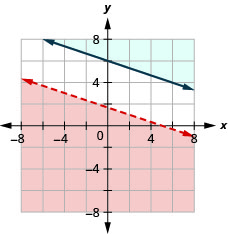
{y≥2x−5−6x+3y>−4
Solve Applications of Systems of Inequalities
In the following exercises, translate to a system of inequalities and solve.
Roxana makes bracelets and necklaces and sells them at the farmers’ market. She sells the bracelets for $12 each and the necklaces for $18 each. At the market next weekend she will have room to display no more than 40 pieces, and she needs to sell at least $500 worth in order to earn a profit.
- Write a system of inequalities to model this situation.
- Graph the system.
- Should she display 26 bracelets and 14 necklaces?
- Should she display 39 bracelets and 1 necklace?
- Answer
-
- {b+n≤4012b+18n≥500
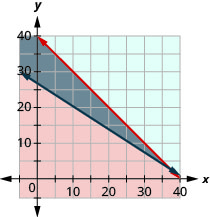
3. yes
4. no
Annie has a budget of $600 to purchase paperback books and hardcover books for her classroom. She wants the number of hardcover to be at least 5 more than three times the number of paperback books. Paperback books cost $4 each and hardcover books cost $15 each.
- Write a system of inequalities to model this situation.
- Graph the system.
- Can she buy 8 paperback books and 40 hardcover books?
- Can she buy 10 paperback books and 37 hardcover books?
Practice Test
{x−4y=−82x+5y=10
- (0,2)
- (4,3)
- Answer
-
- yes
- no
In the following exercises, solve the following systems by graphing.
{x−y=5x+2y=−4
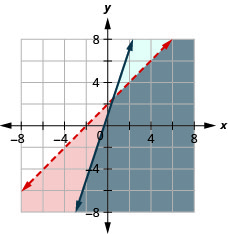
{x−y>−2y≤3x+1
- Answer
-
In the following exercises, solve each system of equations. Use either substitution or elimination.
{3x−2y=3y=2x−1
{x+y=−3x−y=11
- Answer
-
(4,−7)
{4x−3y=75x−2y=0
{y=−45x+18x+10y=10
- Answer
-
infinitely many solutions
{2x+3y=12−4x+6y=−16
In the following exercises, translate to a system of equations and solve.
The sum of two numbers is −24. One number is 104 less than the other. Find the numbers.
- Answer
-
The numbers are 40 and 64
Ramon wants to plant cucumbers and tomatoes in his garden. He has room for 16 plants, and he wants to plant three times as many cucumbers as tomatoes. How many cucumbers and how many tomatoes should he plant?
Two angles are complementary. The measure of the larger angle is six more than twice the measure of the smaller angle. Find the measures of both angles.
- Answer
-
The measures of the angles are 28 degrees and 62 degrees.
On Monday, Lance ran for 30 minutes and swam for 20 minutes. His fitness app told him he had burned 610 calories. On Wednesday, the fitness app told him he burned 695 calories when he ran for 25 minutes and swam for 40 minutes. How many calories did he burn for one minute of running? How many calories did he burn for one minute of swimming?
Kathy left home to walk to the mall, walking quickly at a rate of 4 miles per hour. Her sister Abby left home 15 minutes later and rode her bike to the mall at a rate of 10 miles per hour. How long will it take Abby to catch up to Kathy?
- Answer
-
It will take Kathy 16 of an hour (or 10 minutes)
It takes 512 hours for a jet to fly 2,475 miles with a headwind from San Jose, California to Lihue, Hawaii. The return flight from Lihue to San Jose with a tailwind, takes 5 hours. Find the speed of the jet in still air and the speed of the wind.
Liz paid $160 for 28 tickets to take the Brownie troop to the science museum. Children’s tickets cost $5 and adult tickets cost $9. How many children’s tickets and how many adult tickets did Liz buy?
- Answer
-
Liz bought 23 children’s tickets and 5 adult tickets.
A pharmacist needs 20 liters of a 2% saline solution. He has a 1% and a 5% solution available. How many liters of the 1% and how many liters of the 5% solutions should she mix to make the 2% solution?
Translate to a system of inequalities and solve.
Andi wants to spend no more than $50 on Halloween treats. She wants to buy candy bars that cost $1 each and lollipops that cost $0.50 each, and she wants the number of lollipops to be at least three times the number of candy bars.
- Write a system of inequalities to model this situation.
- Graph the system.
- Can she buy 20 candy bars and 70 lollipops?
- Can she buy 15 candy bars and 65 lollipops?
- Answer
-
- {C+0.5L≤50L≥3C
3. No
4. Yes


