9.8E: Exercises
- Page ID
- 30282
Practice Makes Perfect
Simplify Expressions with \(a^{\frac{1}{n}}\)
In the following exercises, write as a radical expression.
- \(x^{\frac{1}{2}}\)
- \(y^{\frac{1}{3}}\)
- \(z^{\frac{1}{4}}\)
- \(r^{\frac{1}{2}}\)
- \(s^{\frac{1}{3}}\)
- \(t^{\frac{1}{4}}\)
- Answer
-
- \(\sqrt{r}\)
- \(\sqrt[3]{s}\)
- \(\sqrt[4]{t}\)
- \(u^{\frac{1}{5}}\)
- \(v^{\frac{1}{9}}\)
- \(w^{\frac{1}{20}}\)
- \(g^{\frac{1}{7}}\)
- \(h^{\frac{1}{5}}\)
- \(j^{\frac{1}{25}}\)
- Answer
-
- \(\sqrt[7]{g}\)
- \(\sqrt[5]{h}\)
- \(\sqrt[25]{j}\)
- \(−\sqrt[7]{x}\)
- \(\sqrt[9]{y}\)
- \(\sqrt[5]{f}\)
- \(\sqrt[8]{r}\)
- \(\sqrt[10]{s}\)
- \(\sqrt[4]{t}\)
- Answer
-
- \(r^{\frac{1}{8}}\)
- \(s^{\frac{1}{10}}\)
- \(t^{\frac{1}{4}}\)
- \(\sqrt[3]{a}\
- \(\sqrt[12]{b}\)
- \(\sqrt{c}\)
- \(\sqrt[5]{u}\)
- \(\sqrt{v}\)
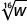
- Answer
-
- \(u^{\frac{1}{5}}\)
- \(v^{\frac{1}{2}}\)
- \(w^{\frac{1}{16}}\)
- \(\sqrt[3]{7c}\)
- \(\sqrt[7]{12d}\)
- \(3\sqrt[4]{5f}\)
- \(\sqrt[4]{5x}\)
- \(\sqrt[8]{9y}\)
- \(7\sqrt[5]{3z}\)
- Answer
-
- \((5x)^{\frac{1}{4}}\)
- \((9y)^{\frac{1}{8}}\)
- \(7(3z)^{\frac{1}{5}}\)
- \(\sqrt{21p}\)
- \(\sqrt[4]{8q}\)
- \(\sqrt[6]{436r}\)
- \(\sqrt[3]{25a}\)
- \(\sqrt{3b}\)
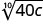
- Answer
-
- \((25a)^{\frac{1}{3}}\)
- \((3b)^{\frac{1}{2}}\)
- \((40c)^{\frac{1}{10}}\)
In the following exercises, simplify.
- \(81^{\frac{1}{2}}\)
- \(125^{\frac{1}{3}}\)
- \(64^{\frac{1}{2}}\)
- \(625^{\frac{1}{4}}\)
- \(243^{\frac{1}{5}}\)
- \(32^{\frac{1}{5}}\)
- Answer
-
- 5
- 3
- 2
- \(16^{\frac{1}{4}}\)
- \(16^{\frac{1}{2}}\)
- \(3125^{\frac{1}{5}}\)
- \(216^{\frac{1}{3}}\)
- \(32^{\frac{1}{5}}\)
- \(81^{\frac{1}{4}}\)
- Answer
-
- 6
- 2
- 3
- \((−216)^{\frac{1}{3}}\)
- \(−216^{\frac{1}{3}}\)
- \((216)^{−\frac{1}{3}}\)
- \((−243)^{\frac{1}{5}}\)
- \(−243^{\frac{1}{5}}\)
- \((243)^{−\frac{1}{5}}\)
- Answer
-
- −3
- −3
- \(\frac{1}{3}\)
- \((−1)^{\frac{1}{3}}\)
- \(−1^{\frac{1}{3}}\)
- \((1)^{−\frac{1}{3}}\)
- \((−1000)^{\frac{1}{3}}\)
- \(−1000^{\frac{1}{3}}\)
- \((1000)^{−\frac{1}{3}}\)
- Answer
-
- −10
- −10
- \(\frac{1}{10}
- \((−81)^{\frac{1}{4}}\)
- \(−81^{\frac{1}{4}}\)
- \((81)^{−\frac{1}{4}}\)
- \((−49)^{\frac{1}{2}}\)
- \(−49^{\frac{1}{2}}\)
- \((49)^{−\frac{1}{2}}\)
- Answer
-
- not a real number
- −7
- \(\frac{1}{7}\)
- \((−36)^{\frac{1}{2}}\)
- \(−36^{\frac{1}{2}}\)
- \((36)^{−\frac{1}{2}}\)
- \((−1)^{\frac{1}{4}}\)
- \((1)^{−\frac{1}{4}}\)
- \(−1^{\frac{1}{4}}\)
- Answer
-
- not a real number
- 1
- −1
- \((−100)^{\frac{1}{2}}\)
- \(−100^{\frac{1}{2}}\)
- \((100)^{−\frac{1}{2}}\)
- \((−32)^{\frac{1}{5}}\)
- \((243)^{−\frac{1}{5}}\)
- \(−125^{\frac{1}{3}}\)
- Answer
-
- −2
- \(\frac{1}{3}\)
- −5
Simplify Expressions with \(a^{\frac{m}{n}}\)
In the following exercises, write with a rational exponent.
- \(\sqrt{m^5}\)
- \(\sqrt[3]{n^2}\)
- \(\sqrt[4]{p^3}\)
- \(\sqrt[4]{r^7}\)
- \(\sqrt[5]{s^3}\)
- \(\sqrt[3]{t^7}\)
- Answer
-
- \(r^{\frac{7}{4}}\)
- \(s^{\frac{3}{5}}\)
- \(t^{\frac{7}{3}}\)
- \(\sqrt[5]{u^2}\)
- \(\sqrt[5]{v^8}\)
- \(\sqrt[9]{w^4}\)
- \(\sqrt[3]{a}\)
- \(\sqrt[5]{b}\)
- \(\sqrt[3]{c^5}\)
- Answer
-
- \(a^{\frac{1}{3}}\)
- \(b^{\frac{1}{5}}\)
- \(c^{\frac{5}{3}}\)
- \(16^{\frac{3}{2}}\)
- \(8^{\frac{2}{3}}\)
- \(10,000^{\frac{3}{4}}\)
- \(1000^{\frac{2}{3}}\)
- \(25^{\frac{3}{2}}\)
- \(32^{\frac{3}{5}}\)
- Answer
-
- 100
- 125
- 8
- \(275^{\frac{3}{2}}\)
- \(16^{\frac{5}{4}}\)
- \(32^{\frac{2}{5}}\)
- \(16^{\frac{3}{2}}\)
- \(125^{\frac{5}{3}}\)
- \(64^{\frac{4}{3}}\)
- Answer
-
- 64
- 3125
- 256
- \(32^{\frac{2}{5}}\)
- \(27^{−\frac{2}{3}}\)
- \(25^{−\frac{3}{2}}\)
- \(64^{\frac{5}{2}}\)
- \(81^{−\frac{3}{2}}\)
- \(27^{−\frac{4}{3}}\)
- Answer
-
- 32,768
- \(\frac{1}{729}\)
- \(\frac{1}{81}\)
- \(25^{\frac{3}{2}}\)
- \(9^{−\frac{3}{2}}\)
- \((−64)^{\frac{2}{3}}\)
- \(100^{\frac{3}{2}}\)
- \(49^{−\frac{5}{2}}\)
- \((−100)^{\frac{3}{2}}\)
- Answer
-
- 1000
- \(\frac{1}{16,807}\)
- not a real numbe
- \(−9^{\frac{3}{2}}\)
- \(−9^{−\frac{3}{2}}\)
- \((−9)^{\frac{3}{2}}\)
- \(−64^{\frac{3}{2}}\)
- \(−64^{−\frac{3}{2}}\)
- \((−64)^{\frac{3}{2}}\)
- Answer
-
- −512
- \(−\frac{1}{512}\)
- not a real number
- \(−100^{\frac{3}{2}}\)
- \(−100^{−\frac{3}{2}}\)
- \((−100)^{\frac{3}{2}}\)
- \(−49^{\frac{3}{2}}\)
- \(−49^{−\frac{3}{2}}\)
- \((−49)^{\frac{3}{2}}\)
- Answer
-
- −343
- \(−\frac{1}{343}\)
- not a real number
Use the Laws of Exponents to Simplify Expressions with Rational Exponents
In the following exercises, simplify.
- \(4^{\frac{5}{8}}·4^{\frac{11}{8}}\)
- \(m^{\frac{7}{12}}·m^{\frac{17}{12}}\)
- \(p^{\frac{3}{7}}·p^{\frac{18}{7}}\)
- \(6^{\frac{5}{2}}·6^{\frac{12}{6}}\)
- \(n^{\frac{2}{10}}·n^{\frac{8}{10}}\)
- \(q^{\frac{2}{5}}·q^{\frac{13}{5}}\)
- Answer
-
- 216
- n
- \(q^3\)
- \(5^{\frac{1}{2}}·5^{\frac{7}{2}}\)
- \(c^{\frac{3}{4}}·c^{\frac{9}{4}}\)
- \(d^{\frac{3}{5}}·d^{\frac{2}{5}}\)
- \(10^{\frac{1}{3}}·10^{\frac{5}{3}}\)
- \(x^{\frac{5}{6}}·x^{\frac{7}{6}}\)
- \(y^{\frac{11}{8}}·y^{\frac{21}{8}}\)
- Answer
-
- 100
- \(x^2\)
- \(y^4\)
- \((m^6)^{\frac{5}{2}}\)
- \((n^9)^{\frac{4}{3}}\)
- \((p^{12})^{\frac{3}{4}}\)
- \((a^{12})^{\frac{1}{6}}\)
- \((b^{15})^{\frac{3}{5}}\)
- \((c^{11})^{\frac{1}{11}}\)
- Answer
-
- \(a^2\)
- \(b^9\)
- c
- \((x^{12})^{\frac{2}{3}}\)
- \((y^{20})^{\frac{2}{5}}\)
- \((z^{16})^{\frac{1}{16}}\)
- \((h^6)^{\frac{4}{3}}\)
- \((k^{12})^{\frac{3}{4}}\)
- \((j^{10})^{\frac{7}{5}}\)
- Answer
-
- \(h^8\)
- \(k^9\)
- \(j^{14}\)
- \(\frac{x^{\frac{7}{2}}}{x^{\frac{5}{2}}}\)
- \(\frac{y^{\frac{5}{2}}}{y^{\frac{1}{2}}}\)
- \(\frac{r^{\frac{4}{5}}}{r^{\frac{9}{5}}}\)
- \(\frac{s^{\frac{11}{5}}}{s^{\frac{6}{5}}}\)
- \(\frac{z^{\frac{7}{3}}}{z^{\frac{1}{3}}}\)
- \(\frac{w^{\frac{2}{7}}}{w^{\frac{9}{7}}}\)
- Answer
-
- s
- \(z^2\)
- \(\frac{1}{w}\)
- \(\frac{t^{\frac{12}{5}}}{t^{\frac{7}{5}}}\)
- \(\frac{x^{\frac{3}{2}}}{x^{\frac{1}{2}}}\)
- \(\frac{m^{\frac{13}{8}}}{m^{\frac{5}{8}}}\)
- \(\frac{u^{\frac{13}{9}}}{u^{\frac{4}{9}}}\)
- \(\frac{r^{\frac{15}{7}}}{r^{\frac{8}{7}}}\)
- \(\frac{n^{\frac{3}{5}}}{n^{\frac{8}{5}}}\)
- Answer
-
- u
- r
- \(\frac{1}{n}\)
- \((9p^{\frac{2}{3}})^{\frac{5}{2}}\)
- \((27q^{\frac{3}{2}})^{\frac{4}{3}}\)
- \((81r^{\frac{4}{5}})^{\frac{1}{4}}\)
- \((64s^{\frac{3}{7}})^{\frac{1}{6}}\)
- Answer
-
- \(3r^{\frac{1}{5}}\)
- \(2s^{\frac{1}{14}}\)
- \((16u^{\frac{1}{3}})^{\frac{3}{4}}\)
- \((100v^{\frac{2}{5}})^{\frac{3}{2}}\)
- \((27m^{\frac{3}{4}})^{\frac{2}{3}}\)
- \((625n^{\frac{8}{3}})^{\frac{3}{4}}\)
- Answer
-
- \(9m^{\frac{1}{2}}\)
- \(125n^2\)
- \((x^{8}y^{10})^{\frac{1}{2}}\)
- \((a^{9}by ^{12})^{\frac{1}{3}}\)
- \((r^{8}s^{4})^{\frac{1}{4}}\)
- \((u^{15}v^{20})^{\frac{1}{5}}\)
- Answer
-
- \(r^{2}s\)
- \(u^{3}v^{4}\)
- \((a^{6}b^{16})^{\frac{1}{2}}\)
- \((j^{9}k^{6})^{\frac{2}{3}}\)
- \((r^{16}s^{10})^{\frac{1}{2}}\)
- \((u^{10}v^5)^{\frac{4}{5}}\)
- Answer
-
- \(r^{8}s^{5}\)
- \(u^{8}v^{4}\)
- \(\frac{r^{\frac{5}{2}}·r^{−\frac{1}{2}}}{r^{−\frac{3}{2}}}\)
- \(\frac{s^{\frac{1}{5}}·s}{s^{−\frac{9}{5}}}\)
- \(\frac{a^{\frac{3}{4}}·a^{−\frac{1}{4}}}{a^{−\frac{10}{4}}}\)
- \(\frac{b^{\frac{2}{3}}·b}{b^{−\frac{7}{3}}}\)
- Answer
-
- \(a^3\)
- \(b^4\)
- \(\frac{c^{\frac{5}{3}}·c^{−\frac{1}{3}}}{c^{−\frac{2}{3}}}\)
- \(\frac{d^{\frac{3}{5}}·d}{d^{−\frac{2}{5}}}\)
- \(\frac{m^{\frac{7}{4}}·m^{−\frac{5}{4}}}{m^{−\frac{2}{4}}}\)
- \(\frac{n^{\frac{3}{7}}·n}{n^{−\frac{4}{7}}}\)
- Answer
-
- m
- \(n^2\)
\(4^{\frac{5}{2}}·4^{\frac{1}{2}}\)
\(n^{\frac{2}{6}}·n^{\frac{4}{6}}\)
- Answer
-
n
\((a^24)^ {\frac{1}{6}}\)
\((b^{10})^{\frac{3}{5}}\)
- Answer
-
\(b^6\)
\(\frac{w^{\frac{2}{5}}}{w^{\frac{7}{5}}}\)
\(\frac{z^{\frac{2}{3}}}{z^{\frac{8}{3}}}\)
- Answer
-
\(\frac{1}{z^2}\)
\((27r^{\frac{3}{5}})^{\frac{1}{3}}\)
\((64s^{\frac{3}{5}})^{\frac{1}{6}}\)
- Answer
-
\(2s^{\frac{1}{10}}\)
\((r^{9}s^{12})^{\frac{1}{3}}\)
\((u^{12}v^{18})^{\frac{1}{6}}\)
- Answer
-
\(u^{2}v^{3}\)
Everyday Math
Landscaping Joe wants to have a square garden plot in his backyard. He has enough compost to cover an area of 144 square feet. Simplify \(144^{\frac{1}{2}}\) to find the length of each side of his garden.
Landscaping Elliott wants to make a square patio in his yard. He has enough concrete to pave an area of 242 square feet. Simplify \(242^{\frac{1}{2}}\) to find the length of each side of his patio.Round to the nearest tenth of a foot.
- Answer
-
15.6 feet
Gravity While putting up holiday decorations, Bob dropped a decoration from the top of a tree that is 12 feet tall. Simplify \(\frac{12^{\frac{1}{2}}}{16^{\frac{1}{2}}}\) to find how many seconds it took for the decoration to reach the ground. Round to the nearest tenth of a second.
Gravity An airplane dropped a flare from a height of 1024 feet above a lake. Simplify \(\frac{1024^{\frac{1}{2}}}{16^{\frac{1}{2}}}\) to find how many seconds it took for the flare to reach the water.
- Answer
-
8 seconds
Writing Exercises
Show two different algebraic methods to simplify \(4^{\frac{3}{2}}\). Explain all your steps.
Explain why the expression \((−16)^{\frac{3}{2}}\) cannot be evaluated.


