Chapter 9 Review Exercises
- Page ID
- 30583
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Chapter 9 Review Exercises
Simplify and Use Square Roots
Simplify Expressions with Square Roots
In the following exercises, simplify.
\(\sqrt{64}\)
\(\sqrt{144}\)
- Answer
-
12
\(−\sqrt{25}\)
\(−\sqrt{81}\)
- Answer
-
−9
\(\sqrt{−9}\)
\(\sqrt{−36}\)
- Answer
-
not a real number
\(\sqrt{64}+\sqrt{225}\)
\(\sqrt{64+225}\)
- Answer
-
17
In the following exercises, estimate each square root between two consecutive whole numbers.
\(\sqrt{28}\)
\(\sqrt{155}\)
- Answer
-
\(12<\sqrt{155}<13\)
Approximate Square Roots
In the following exercises, approximate each square root and round to two decimal places.
\(\sqrt{15}\)
\(\sqrt{57}\)
- Answer
-
7.55
Simplify Variable Expressions with Square Roots
In the following exercises, simplify.
\(\sqrt{q^2}\)
\(\sqrt{64b^2}\)
- Answer
-
8b
\(−\sqrt{121a^2}\)
\(\sqrt{225m^{2}n^{2}}\)
- Answer
-
15mn
\(−\sqrt{100q^2}\)
\(\sqrt{49y^2}\)
- Answer
-
7y
\(\sqrt{4a^{2}b^{2}}\)
\(\sqrt{121c^{2}d^{2}}\)
- Answer
-
11cd
Simplify Square Roots
Use the Product Property to Simplify Square Roots
In the following exercises, simplify.
\(\sqrt{300}\)
\(\sqrt{98}\)
- Answer
-
\(7\sqrt{2}\)
\(\sqrt{x^{13}}\)
\(\sqrt{y^{19}}\)
- Answer
-
\(y^{9}\sqrt{y}\)
\(\sqrt{16m^4}\)
\(\sqrt{36n^{13}}\)
- Answer
-
\(6n^{6}\sqrt{n}\)
\(\sqrt{288m^{21}}\)
\(\sqrt{150n^7}\)
- Answer
-
\(5n^3\sqrt{6n}\)
\(\sqrt{48r^{5}s^{4}}\)
\(\sqrt{108r^{5}s^{3}}\)
- Answer
-
\(6r^{2}s\sqrt{3rs}\)
\(\frac{10−\sqrt{50}}{5}\)
\(\frac{6+\sqrt{72}}{6}\)
- Answer
-
\(1+\sqrt{2}\)
In the following exercises, simplify.
\(\sqrt{\frac{16}{25}}\)
\(\sqrt{\frac{81}{36}}\)
- Answer
-
\(\frac{3}{2}\)
\(\sqrt{\frac{x^8}{x^4}}\)
\(\sqrt{\frac{y^6}{y^2}}\)
- Answer
-
\(y^2\)
\(\sqrt{\frac{98p^6}{2p^2}}\)
\(\sqrt{\frac{72q^8}{2q^4}}\)
- Answer
-
\(6q^2\)
\(\sqrt{\frac{65}{121}}\)
\(\sqrt{\frac{26}{169}}\)
- Answer
-
\(\frac{\sqrt{26}}{13}\)
\(\sqrt{\frac{64x^4}{25x^2}}\)
\(\sqrt{\frac{36r^{10}}{16r^5}}\)
- Answer
-
\(\frac{3r^2\sqrt{r}}{2}\)
\(\sqrt{\frac{48p^{3}q^{5}}{27pq}}\)
\(\sqrt{\frac{12r^{5}s^{7}}{75r^{2}s}}\)
- Answer
-
\(\frac{2rs^3\sqrt{r}}{5}\)
Add and Subtract Square Roots
Add and Subtract Like Square Roots
In the following exercises, simplify.
\(3\sqrt{2}+\sqrt{2}\)
\(5\sqrt{5}+7\sqrt{5}\)
- Answer
-
\(12\sqrt{5}\)
\(4\sqrt{y}+4\sqrt{y}\)
\(6\sqrt{m}−2\sqrt{m}\)
- Answer
-
\(4\sqrt{m}\)
\(−3\sqrt{7}+2\sqrt{7}−\sqrt{7}\)
\(8\sqrt{13}+2\sqrt{3}+3\sqrt{13}\)
- Answer
-
\(11\sqrt{13}+2\sqrt{3}\)
\(3\sqrt{5xy}−\sqrt{5xy}+3\sqrt{5xy}\)
\(2\sqrt{3rs}+\sqrt{3rs}−5\sqrt{rs}\)
- Answer
-
\(3\sqrt{3rs}−5\sqrt{rs}\)
Add and Subtract Square Roots that Need Simplification
In the following exercises, simplify.
\(\sqrt{32}+3\sqrt{2}\)
\(\sqrt{8}+\sqrt{32}\)
- Answer
-
\(5\sqrt{2}\)
\(\sqrt{72}+\sqrt{50}\)
\(\sqrt{48}+\sqrt{75}\)
- Answer
-
\(9\sqrt{3}\)
\(3\sqrt{32}+\sqrt{98}\)
\(\frac{1}{3}\sqrt{27}−\frac{1}{8}\sqrt{192}\)
- Answer
-
0
\(\sqrt{50y^5}−\sqrt{72y^5}\)
Add exercises text here.
- Answer
-
\(17n^2\sqrt{2}\)
Multiply Square Roots
In the following exercises, simplify.
\(\sqrt{2}·\sqrt{20}\)
\(2\sqrt{2}·6\sqrt{14}\)
- Answer
-
\(24\sqrt{7}\)
\(\sqrt{2m^2}·\sqrt{20m^4}\)
\((\sqrt{62y})(\sqrt{350y^3})\)
- Answer
-
\(180y^2\)
\((6\sqrt{3v^4})(5\sqrt{30v})\)
\((\sqrt{8})^2\)
- Answer
-
8
\((−\sqrt{10})^2\)
\((2\sqrt{5})(5\sqrt{5})\)
- Answer
-
50
\((−3\sqrt{3})(5\sqrt{18})\)
In the following exercises, simplify.
\(10(2−\sqrt{7})\)
- Answer
-
\(20−10\sqrt{7}\)
\(\sqrt{3}(4+\sqrt{12})\)
\((5+\sqrt{2})(3−\sqrt{2})\)
- Answer
-
\(13−2\sqrt{2}\)
\((5−3\sqrt{7})(1−2\sqrt{7})\)
\((1−3\sqrt{x})(5+2\sqrt{x})\)
- Answer
-
\(5−13\sqrt{x}−6x\)
\((3+4\sqrt{y})(10−\sqrt{y})\)
\((1+6\sqrt{p})^2\)
- Answer
-
\(1+12\sqrt{p}+36p\)
\((2−6\sqrt{5})^2\)
\((3+2\sqrt{7})(3−2\sqrt{7})\)
- Answer
-
−19
\((6−\sqrt{11})(6+\sqrt{11})\)
Divide Square Roots
Divide Square Roots
In the following exercises, simplify.
\(\frac{\sqrt{75}}{10}\)
- Answer
-
\(\frac{\sqrt{3}}{2}\)
\(\frac{2−\sqrt{12}}{6}\)
\(\frac{\sqrt{48}}{\sqrt{27}}\)
- Answer
-
\(\frac{4}{3}\)
\(\frac{\sqrt{75x^7}}{\sqrt{3x^3}}\)
\(\frac{\sqrt{20y^5}}{\sqrt{2y}}\)
- Answer
-
\(y^2\sqrt{10}\)
\(\frac{\sqrt{98p^{6}q^{4}}}{\sqrt{2p^{4}q^{8}}}\)
In the following exercises, rationalize the denominator.
\(\frac{10}{\sqrt{15}}\)
- Answer
-
\(\frac{2\sqrt{15}}{3}\)
\(\frac{6}{\sqrt{6}}\)
\(\frac{5}{3\sqrt{5}}\)
- Answer
-
\(\frac{\sqrt{5}}{3}\)
\(\frac{10}{2\sqrt{6}}\)
\(\sqrt{\frac{3}{28}}\)
- Answer
-
\(\frac{\sqrt{21}}{14}\)
\(\sqrt{\frac{9}{75}}\)
In the following exercises, rationalize the denominator.
\(\frac{4}{4+\sqrt{27}}\)
- Answer
-
\(\frac{16−12\sqrt{3}}{−11}\)
\(\frac{5}{2−\sqrt{10}}\)
\(\frac{4}{2−\sqrt{5}}\)
- Answer
-
\(−8−4\sqrt{5}\)
\(\frac{5}{4−\sqrt{8}}\)
\(\frac{\sqrt{2}}{\sqrt{p}+\sqrt{3}}\)
- Answer
-
\(\frac{\sqrt{2p}−\sqrt{6}}{p−3}\)
\(\frac{\sqrt{x}−\sqrt{2}}{\sqrt{x}+\sqrt{2}}\)
Solve Equations with Square Roots
Solve Radical Equations
In the following exercises, solve the equation.
\(\sqrt{7z+1}=6\)
- Answer
-
5
\(\sqrt{4u−2}−4=0\)
\(\sqrt{6m+4}−5=0\)
- Answer
-
\(\frac{7}{2}\)
\(\sqrt{2u−3}+2=0\)
\(\sqrt{u−4}+4=u\)
- Answer
-
no solution
\(\sqrt{v−9}+9=0\)
\(\sqrt{r−4}−r=−10\)
- Answer
-
13
\(\sqrt{s−9}−s=−9\)
\(2\sqrt{2x−7}−4=8\)
- Answer
-
\(\frac{43}{2}\)
\(\sqrt{2−x}=\sqrt{2x−7}\)
\(\sqrt{a}+3=\sqrt{a+9}\)
- Answer
-
0
\(\sqrt{r}+3=\sqrt{r+4}\)
\(\sqrt{u}+2=\sqrt{u+5}\)
- Answer
-
\(\frac{11}{6}\)
\(\sqrt{n+11}−1=\sqrt{n+4}\)
\(\sqrt{y+5}+1=\sqrt{2y+3}\)
- Answer
-
11
In the following exercises, solve. Round approximations to one decimal place.
A pallet of sod will cover an area of about 600 square feet. Trinh wants to order a pallet of sod to make a square lawn in his backyard. Use the formula \(s=\sqrt{A}\) to find the length of each side of his lawn.
A helicopter dropped a package from a height of 900 feet above a stranded hiker. Use the formula \(t=\frac{\sqrt{h}}{4}\) to find how many seconds it took for the package to reach the hiker.
- Answer
-
7.5 seconds
Officer Morales measured the skid marks of one of the cars involved in an accident. The length of the skid marks was 245 feet. Use the formula \(s=\sqrt{24d}\) to find the speed of the car before the brakes were applied.
Higher Roots
Simplify Expressions with Higher Roots
In the following exercises, simplify.
- \(\sqrt[6]{64}\)
- \(\sqrt[3]{64}\)
- Answer
-
- 2
- 4
- \(\sqrt[3]{−27}\)
- \(\sqrt[4]{−64}\)
- \(\sqrt[9]{d^9}\)
- \(\sqrt[8]{v^8}\)
- Answer
-
- d
- |v|
- \(\sqrt[5]{a^{10}}\)
- \(\sqrt[3]{b^{27}}\)
- \(\sqrt[4]{16x^8}\)
- \(\sqrt[6]{64y^{12}}\)
- Answer
-
- \(2x^2\)
- \(2y^2\)
- \(\sqrt[7]{128r^{14}}\)
- \(\sqrt[4]{81s^{24}}\)
Use the Product Property to Simplify Expressions with Higher Roots
In the following exercises, simplify.
- \(\sqrt[9]{d^9}\)
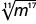
- Answer
-
- d
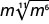
- \(\sqrt[3]{54}\)
- \(\sqrt[4]{128}\)
- \(\sqrt[5]{64c^8}\)
- \(\sqrt[4]{48d^7}\)
- Answer
-
- \(2c\sqrt[5]{2c^3}\)
- \(2d\sqrt[4]{3d^3}\)
- \(\sqrt[3]{343q^7}\)
- \(\sqrt[6]{192r^9}\)
- \(\sqrt[3]{−500}\)
- \(\sqrt[4]{−16}\)
- Answer
-
- \(−5\sqrt[3]{4}\)
- not a real number
In the following exercises, simplify.
\(\sqrt[5]{\frac{r^{10}}{r^5}}\)
\(\sqrt[3]{\frac{w^{12}}{w^2}}\)
- Answer
-
\(w^3\sqrt[3]{w}\)
\(\sqrt[4]{\frac{64y^8}{4y^5}}\)
\(\sqrt[3]{\frac{54z^9}{2z^3}}\)
- Answer
-
\(3z^2\)
\(\sqrt[6]{\frac{64a^7}{b^2}}\)
In the following exercises, simplify.
\(4\sqrt[5]{20}−2\sqrt[5]{20}\)
- Answer
-
\(2\sqrt[5]{20}\)
\(4\sqrt[3]{18}+3\sqrt[3]{18}\)
\(\sqrt[4]{1250}−\sqrt[4]{162}\)
- Answer
-
\(2\sqrt[4]{2}\)
\(\sqrt[3]{640c^5}−\sqrt[3]{−80c^3}\)
\(\sqrt[5]{96t^8}+\sqrt[5]{486t^4}\)
- Answer
-
\(2t^\sqrt[5]{3t^3}+3\sqrt[5]{2t^4}\)
Rational Exponents
Simplify Expressions with \(a^{\frac{1}{n}}\)
In the following exercises, write as a radical expression.
\(r^{\frac{1}{8}}\)
\(s^{\frac{1}{10}}\)
- Answer
-
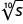
In the following exercises, write with a rational exponent.
\(\sqrt[5]{u}\)
\(\sqrt[6]{v}\)
- Answer
-
\(v^{\frac{1}{6}}\)
\(\sqrt[3]{9m}\)
\(\sqrt[6]{10z}\)
- Answer
-
\((10z)^{\frac{1}{6}}\)
In the following exercises, simplify.
\(16^{\frac{1}{4}}\)
\(32^{\frac{1}{5}}\)
- Answer
-
2
\((−125)^{\frac{1}{3}}\)
\((125)^{−\frac{1}{3}}\)
- Answer
-
\(\frac{1}{5}\)
\((−9)^{\frac{1}{2}}\)
\((36)^{−\frac{1}{2}}\)
- Answer
-
\(\frac{1}{6}\)
In the following exercises, write with a rational exponent.
\(\sqrt[3]{q^5}\)
\(\sqrt[5]{n^8}\)
- Answer
-
\(n^{\frac{8}{5}}\)
In the following exercises, simplify.
\(27^{−\frac{2}{3}}\)
\(64^{\frac{5}{2}}\)
- Answer
-
32,768
\(36^{\frac{3}{2}}\)
\(81^{−\frac{5}{2}}\)
- Answer
-
\(\frac{1}{59,049}\)
Use the Laws of Exponents to Simplify Expressions with Rational Exponents
In the following exercises, simplify.
\(3^{\frac{4}{5}}·3^{\frac{6}{5}}\)
\((x^6)^{\frac{4}{3}}\)
- Answer
-
\(x^8\)
\(\frac{z^{\frac{5}{2}}}{z^{\frac{7}{5}}}\)
\((16s^{\frac{9}{4}})^{\frac{1}{4}}\)
- Answer
-
\(2s^{\frac{9}{16}}\)
\((m^{8}n^{12})^{\frac{1}{4}}\)
\(\frac{z^{\frac{2}{3}}·z^{−\frac{1}{3}}}{z^{−\frac{5}{3}}}\)
- Answer
-
\(z^2\)
Practice Test
In the following exercises, simplify.
\(\sqrt{81+144}\)
\(\sqrt{169m^{4}n^{2}}\)
- Answer
-
\(13m^{2}|n|\)
\(\sqrt{36n^{13}}\)
\(3\sqrt{13}+5\sqrt{2}+\sqrt{13}\)
- Answer
-
\(4\sqrt{13}+5\sqrt{2}\)
\(5\sqrt{20}+2\sqrt{125}\)
\((3\sqrt{6y})(\sqrt{250y^3})\)
- Answer
-
\(180y^2\sqrt{3}\)
\((2−5\sqrt{x})(3+\sqrt{x})\)
\((1−2\sqrt{q})^2\)
- Answer
-
\(1−4\sqrt{q}+4q\)
- \(\sqrt{a^{12}}\)
- \(\sqrt[3]{b^{21}}\)
- \(\sqrt[4]{81x^{12}}\)
- \(\sqrt[6]{64y^{18}}\)
- Answer
-
- \(3x^3\)
- \(2y^3\)
\(\sqrt[6]{\frac{64r^{12}}{25r^6}}\)
\(\sqrt{\frac{14y^3}{7y}}\)
- Answer
-
\(y\sqrt{2}\)
\(\frac{\sqrt{256x^7}}{\sqrt{54x^2}}\)
\(\sqrt[4]{512}−2\sqrt[4]{32}\)
- Answer
-
0
- \(256^{\frac{1}{4}}\)
- \(243^{\frac{1}{5}}\)
\(49^{\frac{3}{2}}\)
- Answer
-
343
\(25^{−\frac{5}{2}}\)
\(\frac{w^{\frac{3}{4}}}{w^{\frac{7}{4}}}\)
- Answer
-
\(\frac{1}{w}\)
\((27s^{\frac{3}{5}})^{\frac{1}{3}}\)
In the following exercises, rationalize the denominator.
\(\frac{3}{2\sqrt{6}}\)
- Answer
-
\(\frac{\sqrt{6}}{4}\)
\(\frac{\sqrt{3}}{\sqrt{x}+\sqrt{5}}\)
In the following exercises, solve.
\(3\sqrt{2x−3}−20=7\)
- Answer
-
42
\(\sqrt{3u−2}=\sqrt{5u+1}\)
In the following exercise, solve.
A helicopter flying at an altitude of 600 feet dropped a package to a lifeboat. Use the formula \(t=\frac{\sqrt{h}}{4}\) to find how many seconds it took for the package to reach the hiker. Round your answer to the nearest tenth of a second.
- Answer
-
6.1 seconds


