9.5: Divide Square Roots
- Page ID
- 15187
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Divide square roots
- Rationalize a one-term denominator
- Rationalize a two-term denominator
Before you get started, take this readiness quiz.
- Find a fraction equivalent to \(\frac{5}{8}\) with denominator 48.
If you missed this problem, review Exercise 1.6.1. - Simplify: \((\sqrt{5})^2\).
If you missed this problem, review Example 9.4.13. - Multiply: (7+3x)(7−3x).
If you missed this problem, review Exercise 6.4.22.
Divide Square Roots
We know that we simplify fractions by removing factors common to the numerator and the denominator. When we have a fraction with a square root in the numerator, we first simplify the square root. Then we can look for common factors.
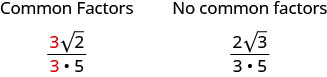
Simplify: \(\frac{\sqrt{54}}{6}\)
- Answer
-
\(\frac{\sqrt{54}}{6}\) Simplify the radical. \(\frac{\sqrt{9}·\sqrt{6}}{6}\) Simplify. \(\frac{3\sqrt{6}}{6}\) Remove the common factors. \(\frac{3\sqrt{6}}{3·2}\) Simplify. \(\frac{\sqrt{6}}{2}\)
Simplify: \(\frac{\sqrt{32}}{8}\).
- Answer
-
\(\frac{\sqrt{2}}{2}\)
Simplify: \(\frac{\sqrt{75}}{15}\).
- Answer
-
\(\frac{\sqrt{3}}{3}\)
Simplify: \(\frac{6−\sqrt{24}}{12}\).
- Answer
-
\(\frac{6−\sqrt{24}}{12}\) Simplify the radical. \(\frac{6−\sqrt{4}·\sqrt{6}}{12}\) Simplify. \(\frac{6−2\sqrt{6}}{12}\) Factor the common factor from the numerator. \(\frac{2(3−\sqrt{6})}{12}\) Remove the common factors. \(\frac{2(3−\sqrt{6})}{2·6}\) Simplify. \(\frac{3−\sqrt{6}}{6}\)
Simplify: \(\frac{8−\sqrt{40}}{10}\).
- Answer
-
\(\frac{4−\sqrt{10}}{5}\)
Simplify: \(\frac{10−\sqrt{75}}{20}\).
- Answer
-
\(\frac{5−\sqrt{3}}{4}\)
We have used the Quotient Property of Square Roots to simplify square roots of fractions. The Quotient Property of Square Roots says
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\), \(b \ne 0\).
Sometimes we will need to use the Quotient Property of Square Roots ‘in reverse’ to simplify a fraction with square roots.
\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\), \(b \ne 0\).
We will rewrite the Quotient Property of Square Roots so we see both ways together. Remember: we assume all variables are greater than or equal to zero so that their square roots are real numbers.
If a, b are non-negative real numbers and \(b \ne 0\), then
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\) and \(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
We will use the Quotient Property of Square Roots ‘in reverse’ when the fraction we start with is the quotient of two square roots, and neither radicand is a perfect square. When we write the fraction in a single square root, we may find common factors in the numerator and denominator.
Simplify: \(\frac{\sqrt{27}}{\sqrt{75}}\)
- Answer
-
\(\frac{\sqrt{27}}{\sqrt{75}}\) Neither radicand is a perfect square, so rewrite using the quotient property of square root. \(\sqrt{\frac{27}{75}}\) Remove common factors in the numerator and denominator. \(\sqrt{\frac{9}{25}}\) Simplify. \(\frac{3}{5}\)
Simplify: \(\frac{\sqrt{48}}{\sqrt{108}}\)
- Answer
-
\(\frac{2}{3}\)
Simplify: \(\frac{\sqrt{96}}{\sqrt{54}}\)
- Answer
-
\(\frac{4}{3}\)
We will use the Quotient Property for Exponents, \(\frac{a^m}{a^n}=a^{m−n}\), when we have variables with exponents in the radicands.
Simplify: \(\frac{\sqrt{6y^5}}{\sqrt{2y}}\)
- Answer
-
\(\frac{\sqrt{6y^5}}{\sqrt{2y}}\) Neither radicand is a perfect square, so rewrite using the quotient property of square root. \(\sqrt{\frac{6y^5}{2y}}\) Remove common factors in the numerator and denominator. \(\sqrt{3y^4}\) Simplify. \(y^2\sqrt{3}\)
Simplify: \(\frac{\sqrt{12r^3}}{\sqrt{6r}}\).
- Answer
-
\(r\sqrt{2}\)
Simplify: \(\frac{\sqrt{14p^9}}{\sqrt{2p^5}}\)
- Answer
-
\(p^2\sqrt{7}\)
Simplify: \(\frac{\sqrt{72x^3}}{\sqrt{162x}}\)
- Answer
-
\(\frac{\sqrt{72x^3}}{\sqrt{162x}}\) Rewrite using the quotient property of square roots. \(\sqrt{\frac{72x^3}{162x}}\) Remove common factors. \(\sqrt{\frac{18·4·x^2·x}{18·9·x}}\) Simplify. \(\sqrt{\frac{4x^2}{9}}\) Simplify the radical. \(\frac{2x}{3}\)
Simplify: \(\frac{\sqrt{50s^3}}{\sqrt{128s}}\).
- Answer
-
\(\frac{5s}{8}\)
Simplify: \(\frac{\sqrt{75q^5}}{\sqrt{108q}}\).
- Answer
-
\(\frac{5q^2}{6}\)
Simplify: \(\frac{\sqrt{147ab^8}}{\sqrt{3a^3b^4}}\).
- Answer
-
\(\frac{\sqrt{147ab^8}}{\sqrt{3a^{3}b^{4}}}\) Rewrite using the quotient property of square roots. \(\sqrt{\frac{147ab^8}{3a^{3}b^{4}}}\) Remove common factors. \(\sqrt{\frac{49b^4}{a^2}}\ Simplify the radical. \(\frac{7b^2}{a}\)
Simplify: \(\frac{\sqrt{162x^{10}y^{2}}}{\sqrt{2x^6y^6}}\).
- Answer
-
\(\frac{9x^2}{y^2}\)
Simplify: \(\frac{\sqrt{300m^{3}n^{7}}}{\sqrt{3m^{5}n}}\).
- Answer
-
\(\frac{10n^3}{m}\)
Rationalize a One Term Denominator
Before the calculator became a tool of everyday life, tables of square roots were used to find approximate values of square roots. Figure shows a portion of a table of squares and square roots. Square roots are approximated to five decimal places in this table.
If someone needed to approximate a fraction with a square root in the denominator, it meant doing long division with a five decimal-place divisor. This was a very cumbersome process.
For this reason, a process called rationalizing the denominator was developed. A fraction with a radical in the denominator is converted to an equivalent fraction whose denominator is an integer. This process is still used today and is useful in other areas of mathematics, too.
The process of converting a fraction with a radical in the denominator to an equivalent fraction whose denominator is an integer is called rationalizing the denominator.
Square roots of numbers that are not perfect squares are irrational numbers. When we rationalize the denominator, we write an equivalent fraction with a rational number in the denominator.
Let’s look at a numerical example.
\[\begin{array}{ll} {\text{Suppose we need an approximate value for the fraction.}}&{\frac{1}{\sqrt{2}}}\\ {\text{A five decimal place approximation to} \sqrt{2} \text{is} 1.41421}&{\frac{1}{1.41421}}\\ {\text{Without a calculator, would you want to do this division?}}&{1.41421) \overline{1.0}}\\ \nonumber \end{array}\]
But we can find a fraction equivalent to \(\frac{1}{\sqrt{2}}\) by multiplying the numerator and denominator by \(\sqrt{2}\).
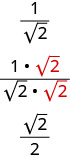
Now if we need an approximate value, we divide \(2) \overline{1.41421}\). This is much easier.
Even though we have calculators available nearly everywhere, a fraction with a radical in the denominator still must be rationalized. It is not considered simplified if the denominator contains a square root.
Similarly, a square root is not considered simplified if the radicand contains a fraction.
A square root is considered simplified if there are
- no perfect-square factors in the radicand
- no fractions in the radicand
- no square roots in the denominator of a fraction
To rationalize a denominator, we use the property that \((\sqrt{a})^2=a\). If we square an irrational square root, we get a rational number.
We will use this property to rationalize the denominator in the next example.
Simplify: \(\frac{4}{\sqrt{3}}\).
- Answer
-
To remove the square root from the denominator, we multiply it by itself. To keep the fractions equivalent, we multiply both the numerator and denominator by the same factor.
\(\frac{4}{\sqrt{3}}\)
Multiply both the numerator and denominator by \(\sqrt{3}\)\(\frac{4·\sqrt{3}}{\sqrt{3}·\sqrt{3}}\) Simplify. \(\frac{4\sqrt{3}}{3}\)
Simplify: \(\frac{5}{\sqrt{3}}\).
- Answer
-
\(\frac{5\sqrt{3}}{3}\)
Simplify: \(\frac{6}{\sqrt{5}}\).
- Answer
-
\(\frac{6\sqrt{5}}{5}\)
Simplify: \(−\frac{8}{3\sqrt{6}}\)
- Answer
-
To remove the square root from the denominator, we multiply it by itself. To keep the fractions equivalent, we multiply both the numerator and denominator by \(\sqrt{6}\).
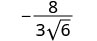
Multiply both the numerator and the denominator by \(\sqrt{6}\). 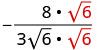
Simplify. 
Remove common factors. 
Simplify. 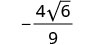
Simplify: \(\frac{5}{2\sqrt{5}}\).
- Answer
-
\(\frac{\sqrt{5}}{2}\)
Simplify: \(−\frac{9}{4\sqrt{3}}\).
- Answer
-
\(−\frac{3\sqrt{3}}{4}\)
Always simplify the radical in the denominator first, before you rationalize it. This way the numbers stay smaller and easier to work with.
Simplify: \(\sqrt{\frac{5}{12}}\).
- Answer
-
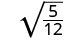
The fraction is not a perfect square, so rewrite using the
Quotient Property.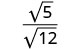
Simplify the denominator. 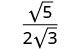
Rationalize the denominator. 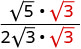
Simplify. 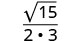
Simplify. 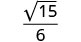
Simplify: \(\sqrt{\frac{7}{18}}\).
- Answer
-
\(\frac{\sqrt{14}}{6}\)
Simplify: \(\sqrt{\frac{3}{32}}\).
- Answer
-
\(\frac{\sqrt{6}}{8}\)
Simplify: \(\sqrt{\frac{11}{28}}\)
- Answer
-
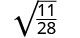
Rewrite using the Quotient Property. 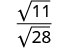
Simplify the denominator. 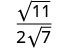
Rationalize the denominator. 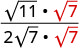
Simplify. 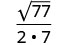
Simplify. 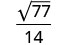
Simplify: \(\sqrt{\frac{3}{27}}\).
- Answer
-
\(\frac{1}{3}\)
Simplify: \(\sqrt{\frac{10}{50}}\)
- Answer
-
\(\frac{\sqrt{5}}{5}\)
Rationalize a Two-Term Denominator
When the denominator of a fraction is a sum or difference with square roots, we use the Product of Conjugates pattern to rationalize the denominator.
\[\begin{array}{ll} {(a−b)(a+b)}&{(2−\sqrt{5})(2+\sqrt{5})}\\ {a^2−b^2}&{2^2−(\sqrt{5})^2}\\ {}&{4−5}\\ {}&{−1}\\ \nonumber \end{array}\]
When we multiply a binomial that includes a square root by its conjugate, the product has no square roots.
Simplify: \(\frac{4}{4+\sqrt{2}}\).
- Answer
-
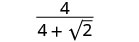
Multiply the numerator and denominator by the conjugate of the denominator. 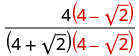
Multiply the conjugates in the denominator. 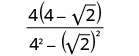
Simplify the denominator. 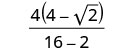
Simplify the denominator. 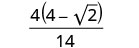
Remove common factors from the numerator and denominator. 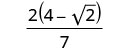
We leave the numerator in factored form to make it easier to look for common factors after we have simplified the denominator.
Simplify: \(\frac{2}{2+\sqrt{3}}\).
- Answer
-
\(\frac{2(2−\sqrt{3})}{1}\)
Simplify: \(\frac{5}{5+\sqrt{3}}\).
- Answer
-
\(\frac{5(5−\sqrt{3})}{22}\)
Simplify: \(\frac{5}{2−\sqrt{3}}\).
- Answer
-
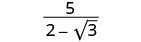
Multiply the numerator and denominator by the conjugate of the denominator. 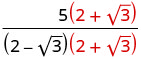
Multiply the conjugates in the denominator. 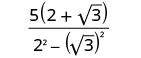
Simplify the denominator. 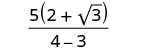
Simplify the denominator. 
Simplify. 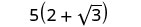
Simplify: \(\frac{3}{1−\sqrt{5}}\).
- Answer
-
\(−\frac{3(1+\sqrt{5})}{4}\)
Simplify: \(\frac{2}{4−\sqrt{6}}\).
- Answer
-
\(\frac{4+\sqrt{6}}{5}\)
Simplify: \(\frac{\sqrt{3}}{\sqrt{u}−\sqrt{6}}\).
- Answer
-
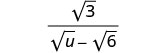
Multiply the numerator and denominator by the conjugate of the denominator. 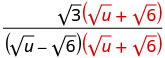
Multiply the conjugates in the denominator. 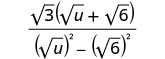
Simplify the denominator. 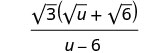
Simplify: \(\frac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).
- Answer
-
\(\frac{\sqrt{5}(\sqrt{x}−\sqrt{2})}{x−2}\)
Simplify: \(\frac{\sqrt{10}}{\sqrt{y}−\sqrt{3}}\).
- Answer
-
\(\frac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y−3}\)
Simplify:\(\frac{\sqrt{x}+\sqrt{7}}{\sqrt{x}−\sqrt{7}}\).
- Answer
-
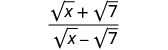
Multiply the numerator and denominator by the conjugate of the denominator. 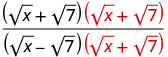
Multiply the conjugates in the denominator. 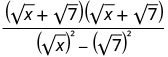
Simplify the denominator. 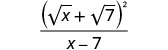
We do not square the numerator. In factored form, we can see there are no common factors to remove from the numerator and denominator.
Simplify: \(\frac{\sqrt{p}+\sqrt{2}}{\sqrt{p}−\sqrt{2}}\).
- Answer
-
\(\frac{(\sqrt{p}+\sqrt{2})^2}{p−2}\)
Simplify: \(\frac{\sqrt{q}−\sqrt{10}}{\sqrt{q}+\sqrt{10}}\).
- Answer
-
\(\frac{(\sqrt{q}−\sqrt{10})^2}{q−10}\)
Access this online resource for additional instruction and practice with dividing and rationalizing.
- Dividing and Rationalizing
Key Concepts
- Quotient Property of Square Roots
- If a, b are non-negative real numbers and \(b \ne 0\), then
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\) and \(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
- If a, b are non-negative real numbers and \(b \ne 0\), then
- Simplified Square Roots
A square root is considered simplified if there are- no perfect square factors in the radicand
- no fractions in the radicand
- no square roots in the denominator of a fraction
Glossary
- rationalizing the denominator
- The process of converting a fraction with a radical in the denominator to an equivalent fraction whose denominator is an integer is called rationalizing the denominator.


