9.4E: Exercises

Practice Makes Perfect

Multiply Square Roots

In the following exercises, simplify.

Example $\PageIndex{48}$

1. $\sqrt{2}·\sqrt{8}$
2. $(3\sqrt{3})(2\sqrt{18})$

Answer

1. $44$
2. $18\sqrt{6}$

Example $\PageIndex{49}$

1. $\sqrt{6}·\sqrt{6}$
2. $(3\sqrt{2})(2\sqrt{32})$

Example $\PageIndex{50}$

1. $\sqrt{7}·\sqrt{14}$
2. $(4\sqrt{8})(5\sqrt{8})$

Answer

1. $7\sqrt{2}$
2. 160

Example $\PageIndex{51}$

1. $\sqrt{6}·\sqrt{12}$
2. $(2\sqrt{5})(2\sqrt{10})$

Example $\PageIndex{52}$

$(5\sqrt{2})(3\sqrt{6})$

Answer

$30\sqrt{3}$

Example $\PageIndex{53}$

$(2\sqrt{3})(4\sqrt{6})$

Example $\PageIndex{54}$

$(−2\sqrt{3})(3\sqrt{18})$

Answer

$−18\sqrt{6}$

Example $\PageIndex{55}$

$(−4\sqrt{5})(5\sqrt{10})$

Example $\PageIndex{56}$

$(5\sqrt{6})(−\sqrt{12})$

Answer

$−30\sqrt{2}$

Example $\PageIndex{57}$

$(6\sqrt{2})(−\sqrt{10})$

Example $\PageIndex{58}$

$(−2\sqrt{7})(−2\sqrt{14})$

Answer

$28\sqrt{2}$

Example $\PageIndex{59}$

$(−2\sqrt{11})(−4\sqrt{22})$

Example $\PageIndex{60}$

1. $(\sqrt{15y})(\sqrt{5y^3})$
2. $(\sqrt{2n^2})(\sqrt{18n^3})$

Answer

1. $5y^2\sqrt{3}$
2. $6n^2\sqrt{n}$

Example $\PageIndex{61}$

1. $(\sqrt{14x^3})(\sqrt{7x^3})$
2. $(\sqrt{3q^2})(\sqrt{48q^3})$

Example $\PageIndex{62}$

1. $(\sqrt{16y^2})(\sqrt{8y^4})$
2. $(\sqrt{11s^6})(\sqrt{11s})$

Answer

1. $8y^3\sqrt{2}$
2. $11s^3\sqrt{s}$

Example $\PageIndex{63}$

ⓐ $(\sqrt{8x^3})(\sqrt{3x})$
ⓑ $(\sqrt{7r})(\sqrt{7r^8})$

Example $\PageIndex{64}$

$(2\sqrt{5b^3})(4\sqrt{15b})$

Answer

$40b^2\sqrt{3}$

Example $\PageIndex{65}$

$(\sqrt{38c^5})(\sqrt{26c^3})$

Example $\PageIndex{66}$

$(6\sqrt{3d^3})(4\sqrt{12d^5})$

Answer

$144d^4$

Example $\PageIndex{67}$

$(2\sqrt{5b^3})(4\sqrt{15b})$

Example $\PageIndex{68}$

$(2\sqrt{5d^6})(3\sqrt{20d^2})$

Answer

$60d^4$

Example $\PageIndex{69}$

$(−2\sqrt{7z^3})(3\sqrt{14z^8})$

Example $\PageIndex{70}$

$(4\sqrt{2k^5})(−3\sqrt{32k^6})$

Answer

$−96k^5\sqrt{k}$

Example $\PageIndex{71}$

1. $(\sqrt{7})^2$
2. $(−\sqrt{15})^2$

Example $\PageIndex{72}$

1. $(\sqrt{11})^2$
2. $(−\sqrt{21})^2$

Answer

1. 11
2. 21

Example $\PageIndex{73}$

1. $(\sqrt{19})^2$
2. $(−\sqrt{5})^2$

Exercise $\PageIndex{74}$

1. $(\sqrt{23})^2$
2. $(−\sqrt{3})^2$

Answer

1. 23
2. 3

Example $\PageIndex{75}$

1. $(4\sqrt{11})(−3\sqrt{11})$
2. $(5\sqrt{3})^2$

Example $\PageIndex{76}$

1. $(2\sqrt{13})(−9\sqrt{13})$
2. $(6\sqrt{5})^2$

Answer

1. −234
2. 180

Example $\PageIndex{77}$

1. $(−3\sqrt{12})(−2\sqrt{6})$
2. $(−4\sqrt{10})^2$

Example $\PageIndex{78}$

1. $(−7\sqrt{5})(−3\sqrt{10})$
2. $(−2\sqrt{14})^2$

Answer

1. $105\sqrt{2}$
2. 56

Use Polynomial Multiplication to Multiply Square Roots

In the following exercises, simplify.

Example $\PageIndex{79}$

1. $3(4−\sqrt{3})$
2. $\sqrt{2}(4−\sqrt{6})$

Example $\PageIndex{80}$

1. $4(6−\sqrt{11})$
2. $\sqrt{2}(5−\sqrt{12})$

Answer

1. $24−4\sqrt{11}$
2. $5\sqrt{2}−2\sqrt{6}$

Example $\PageIndex{81}$

1. $5(3−\sqrt{7})$
2. $\sqrt{3}(4−\sqrt{15})$

Example $\PageIndex{82}$

1. $7(−2−\sqrt{11})$
2. $\sqrt{7}(6−\sqrt{14})$

Answer

1. $−14−7\sqrt{11}$
2. $6\sqrt{7}−7\sqrt{2}$

Example $\PageIndex{83}$

1. $\sqrt{7}(5+2\sqrt{7})$
2. $\sqrt{5}(\sqrt{10}+\sqrt{18})$

Example $\PageIndex{84}$

1. $\sqrt{11}(8+4\sqrt{11})$
2. $\sqrt{3}(\sqrt{12}+\sqrt{27})$

Answer

1. $44+8\sqrt{11}$
2. 15

Example $\PageIndex{85}$

1. $\sqrt{11}(−3+4\sqrt{1})$
2. $\sqrt{3}(\sqrt{15}−\sqrt{18})$

Example $\PageIndex{86}$

1. $\sqrt{2}(−5+9\sqrt{2})$
2. $\sqrt{7}(\sqrt{3}−\sqrt{21})$

Answer

1. $18−5\sqrt{2}$
2. $\sqrt{21}−7\sqrt{3}$

Example $\PageIndex{87}$

$(8+\sqrt{3})(2−\sqrt{3})$

Example $\PageIndex{88}$

$(7+\sqrt{3})(9−\sqrt{3})$

Answer

$60+2\sqrt{3}$

Example $\PageIndex{89}$

$(8−\sqrt{2})(3+\sqrt{2})$

Example $\PageIndex{90}$

$(9−\sqrt{2})(6+\sqrt{2})$

Answer

$52+3\sqrt{2}$

Example $\PageIndex{91}$

$(3−\sqrt{7})(5−\sqrt{7})$

Example $\PageIndex{92}$

$(5−\sqrt{7})(4−\sqrt{7})$

Answer

$27−9\sqrt{7}$

Example $\PageIndex{93}$

$(1+3\sqrt{10})(5−2\sqrt{10})$

Exercise $\PageIndex{94}$

$(7−2\sqrt{5})(4+9\sqrt{5})$

Answer

$−62+55\sqrt{5}$

Example $\PageIndex{95}$

$(\sqrt{3}+\sqrt{10})(\sqrt{3}+2\sqrt{10})$

Example $\PageIndex{96}$

$(\sqrt{11}+\sqrt{5})(\sqrt{11}+6\sqrt{5})$

Answer

$41+7\sqrt{55}$

Example $\PageIndex{97}$

$(2\sqrt{7}−5\sqrt{11})(4\sqrt{7}+9\sqrt{11})$

Example $\PageIndex{98}$

$(4\sqrt{6}+7\sqrt{13})(8\sqrt{6}−3\sqrt{13})$

Answer

$−81+44\sqrt{78}$

Example $\PageIndex{99}$

$(5−\sqrt{u})(3+\sqrt{u})$

Example $\PageIndex{100}$

$(9−\sqrt{w})(2+\sqrt{w})$

Answer

$18+7\sqrt{w}$

Example $\PageIndex{101}$

$(7+2\sqrt{m})(4+9\sqrt{m})$

Example $\PageIndex{102}$

$(6+5\sqrt{n})(11+3\sqrt{n})$

Answer

$66+73\sqrt{n}+15n$

Example $\PageIndex{103}$

1. $(3+\sqrt{5})^2$
2. $(2−5\sqrt{3})^2$

Example $\PageIndex{104}$

1. $(4+\sqrt{11})^2$
2. $(3−2\sqrt{5})^2$

Answer

1. $27+8\sqrt{11}$
2. $29−12\sqrt{5}$

Example $\PageIndex{105}$

1. $(9−\sqrt{6})^2$
2. $(10+3\sqrt{7})^2$

Example $\PageIndex{106}$

1. $(5−\sqrt{10})^2$
2. $(8+3\sqrt{2})^2$

Answer

1. $35−10\sqrt{10}$
2. $82+48\sqrt{2}$

Example $\PageIndex{107}$

$(3−\sqrt{5})(3+\sqrt{5})$

Example $\PageIndex{108}$

$(10−\sqrt{3})(10+\sqrt{3})$

Answer

97

Example $\PageIndex{109}$

$(4+\sqrt{2})(4−\sqrt{2})$

Example $\PageIndex{110}$

$(7+\sqrt{10})(7−\sqrt{10})$

Answer

39

Example $\PageIndex{111}$

$(4+9\sqrt{3})(4−9\sqrt{3})$

Example $\PageIndex{112}$

$(1+8\sqrt{2})(1−8\sqrt{2})$

Answer

−127

Example $\PageIndex{113}$

$(12−5\sqrt{5})(12+5\sqrt{5})$

Example $\PageIndex{114}$

$(9−4\sqrt{3})(9+4\sqrt{3})$

Answer

33

Mixed Practice

In the following exercises, simplify.

Example $\PageIndex{115}$

$\sqrt{3}·\sqrt{21}$

Example $\PageIndex{116}$

$(4\sqrt{6})(−\sqrt{18})$

Answer

$−24\sqrt{3}$

Example $\PageIndex{117}$

$(−5+\sqrt{7})(6+\sqrt{21})$

Example $\PageIndex{118}$

$(−5\sqrt{7})(6\sqrt{21})$

Answer

$−210\sqrt{3}$

Example $\PageIndex{119}$

$(−4\sqrt{2})(2\sqrt{18})$

Example $\PageIndex{120}$

$(\sqrt{35y^3})(\sqrt{7y^3})$

Answer

$7y^3\sqrt{5}$

Example $\PageIndex{121}$

$(4\sqrt{12x^5})(2\sqrt{6x^3})$

Example $\PageIndex{122}$

$(\sqrt{29})^2$

Answer

29

Example $\PageIndex{123}$

$(−4\sqrt{17})(−3\sqrt{17})$

Example $\PageIndex{124}$

$(−4+\sqrt{17})(−3+\sqrt{17})$

Answer

$29−7\sqrt{17}$

Everyday Math

Example $\PageIndex{125}$

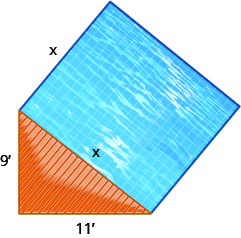
A landscaper wants to put a square reflecting pool next to a triangular deck, as shown below. The triangular deck is a right triangle, with legs of length 9 feet and 11 feet, and the pool will be adjacent to the hypotenuse.

1. Use the Pythagorean Theorem to find the length of a side of the pool. Round your answer to the nearest tenth of a foot.
2. Find the exact area of the pool.

Example $\PageIndex{126}$

An artist wants to make a small monument in the shape of a square base topped by a right triangle, as shown below. The square base will be adjacent to one leg of the triangle. The other leg of the triangle will measure 2 feet and the hypotenuse will be 5 feet.

1. Use the Pythagorean Theorem to find the length of a side of the square base. Round your answer to the nearest tenth of a foot.
   
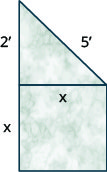
2. Find the exact area of the face of the square base.

Answer

1. 4.6feet
2. 21 sq. feet

Example $\PageIndex{127}$

A square garden will be made with a stone border on one edge. If only $3+\sqrt{10}$ feet of stone are available, simplify $(3+\sqrt{10})^2$ to determine the area of the largest such garden.​​​​​​​

Example $\PageIndex{128}$

A garden will be made so as to contain two square sections, one section with side length $\sqrt{5}+\sqrt{6}$ yards and one section with side length $\sqrt{2}+\sqrt{3}$ yards. Simplify $(\sqrt{5}+\sqrt{6})(\sqrt{2}+\sqrt{3})$ to determine the total area of the garden.

Example $\PageIndex{129}$

Suppose a third section will be added to the garden in the previous exercise. The third section is to have a width of $\sqrt{432}$ feet. Write an expression that gives the total area of the garden.​​

Writing Exercises

Example $\PageIndex{130}$

1. Explain why $(−\sqrt{n})^2$ is always positive, for $n \ge 0$.
2. Explain why $−(\sqrt{n})^2$ is always negative, for $n \ge 0$.

Answer

1. when squaring a negative, it becomes a positive
2. since the negative is not included in the parenthesis, it is not squared, and remains negative​​​​​​​

Example $\PageIndex{131}$

Use the binomial square pattern to simplify $(3+\sqrt{2})^2$. Explain all your steps.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?