10.5: Graphing Quadratic Equations
- Page ID
- 15196
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Recognize the graph of a quadratic equation in two variables
- Find the axis of symmetry and vertex of a parabola
- Find the intercepts of a parabola
- Graph quadratic equations in two variables
- Solve maximum and minimum applications
Before you get started, take this readiness quiz.
Recognize the Graph of a Quadratic Equation in Two Variables
We have graphed equations of the form \(Ax+By=C\). We called equations like this linear equations because their graphs are straight lines.
Now, we will graph equations of the form \(y=ax^2+bx+c\). We call this kind of equation a quadratic equation in two variables.
A quadratic equation in two variables, where a,b,and c are real numbers and \(a\neq 0\), is an equation of the form \[y=ax^2+bx+c \nonumber\]
Just like we started graphing linear equations by plotting points, we will do the same for quadratic equations.
Let’s look first at graphing the quadratic equation \(y=x^2\). We will choose integer values of x between −2 and 2 and find their y values. See Table.
| \(y=x^2\) | |
| x | y |
| 0 | 0 |
| 1 | 1 |
| \(−1\) | 1 |
| 2 | 4 |
| \(−2\) | 4 |
Notice when we let \(x=1\) and \(x=−1\), we got the same value for y.
\[\begin{array} {ll} {y=x^2} &{y=x^2} \\ {y=1^2} &{y=(−1)^2} \\ {y=1} &{y=1} \\ \nonumber \end{array}\]
The same thing happened when we let \(x=2\) and \(x=−2\).
Now, we will plot the points to show the graph of \(y=x^2\). See Figure.
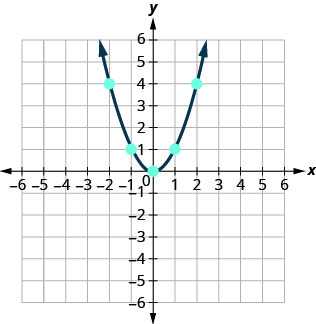
The graph is not a line. This figure is called a parabola. Every quadratic equation has a graph that looks like this.
In Example you will practice graphing a parabola by plotting a few points.
\(y=x^2-1\)
- Answer
-
We will graph the equation by plotting points.
Choose integers values for x, substitute them into the equation and solve for y.Record the values of the ordered pairs in the chart. 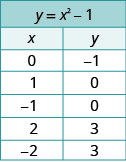
Plot the points, and then connect them with a smooth curve. The result will be the graph of the equation \(y=x^2−1\) 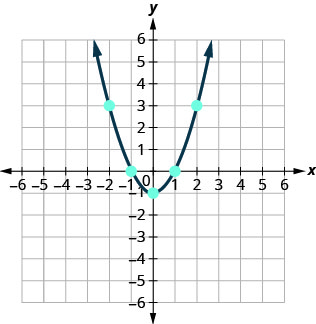
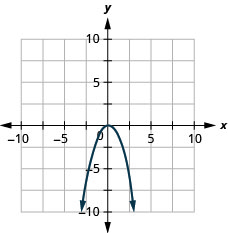
Graph \(y=−x^2\).
- Answer
-
Graph \(y=x^2+1\).
- Answer
-
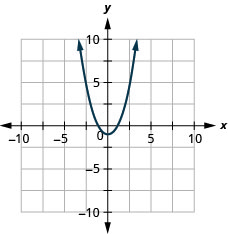
How do the equations \(y=x^2\)and \(y=x^2−1\) differ? What is the difference between their graphs? How are their graphs the same?
All parabolas of the form \(y=ax^2+bx+c\) open upwards or downwards. See Figure.
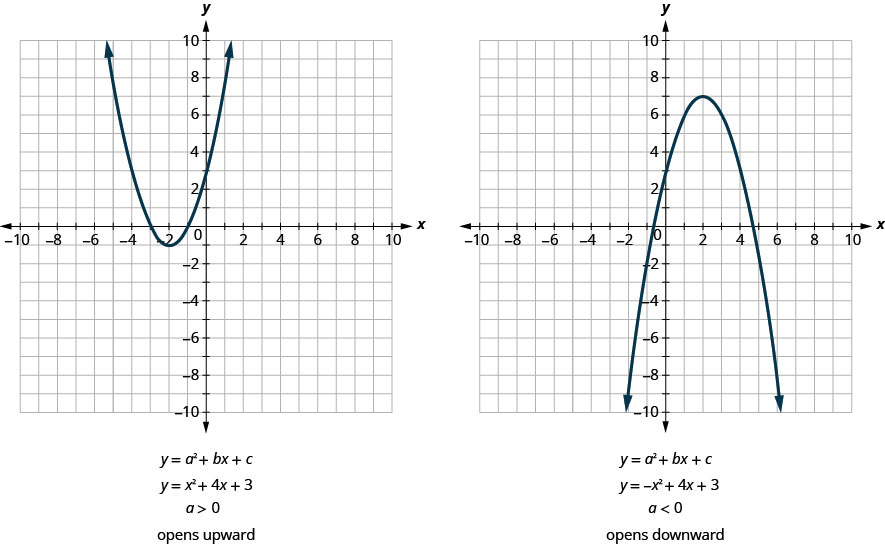
Notice that the only difference in the two equations is the negative sign before the \(x^2\) in the equation of the second graph in Figure. When the \(x^2\) term is positive, the parabola opens upward, and when the \(x^2\) term is negative, the parabola opens downward.
For the quadratic equation \(y=ax^2+bx+c\), if:

Determine whether each parabola opens upward or downward:
- \(y=−3x^2+2x−4\)
- \( y=6x^2+7x−9\)
- Answer
-
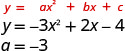
Since the “a” is negative, the parabola will open downward.
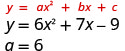
Since the “a” is positive, the parabola will open upward.
Determine whether each parabola opens upward or downward:
- \(y=2x^2+5x−2\)
- \(y=−3x^2−4x+7\)
- Answer
-
- up
- down
Determine whether each parabola opens upward or downward:
- \(y=−2x^2−2x−3\)
- \(y=5x^2−2x−1\)
- Answer
-
- down
- up
Find the Axis of Symmetry and Vertex of a Parabola
Look again at Figure. Do you see that we could fold each parabola in half and that one side would lie on top of the other? The ‘fold line’ is a line of symmetry. We call it the axis of symmetry of the parabola.
We show the same two graphs again with the axis of symmetry in red. See Figure.
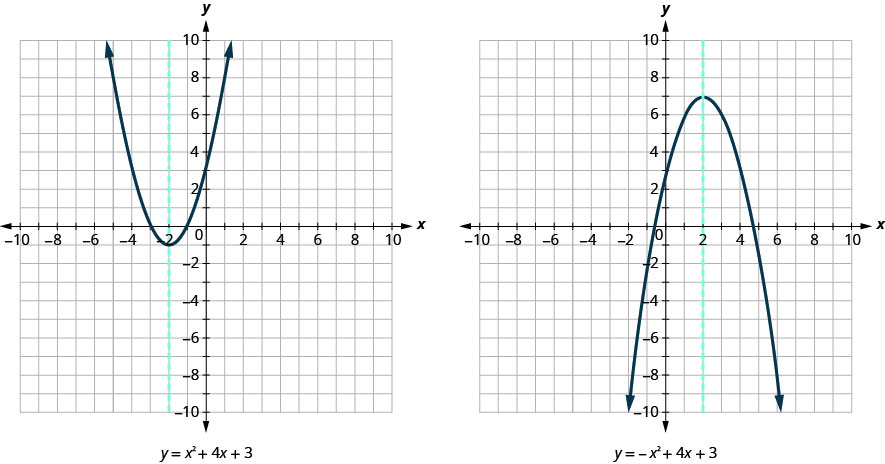
The equation of the axis of symmetry can be derived by using the Quadratic Formula. We will omit the derivation here and proceed directly to using the result. The equation of the axis of symmetry of the graph of \(y=ax^2+bx+c\) is x=\(−\frac{b}{2a}\).
So, to find the equation of symmetry of each of the parabolas we graphed above, we will substitute into the formula x=\(−\frac{b}{2a}\).
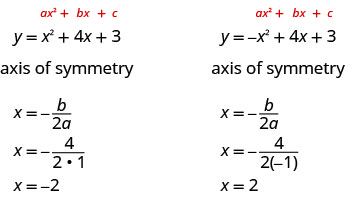
The point on the parabola that is on the axis of symmetry is the lowest or highest point on the parabola, depending on whether the parabola opens upwards or downwards. This point is called the vertex of the parabola.
We can easily find the coordinates of the vertex, because we know it is on the axis of symmetry. This means its x-coordinate is \(−\frac{b}{2a}\). To find the y-coordinate of the vertex, we substitute the value of the x-coordinate into the quadratic equation.

For a parabola with equation \(y=ax^2+bx+c\):
- The axis of symmetry of a parabola is the line x=\(−\frac{b}{2a}\).
- The vertex is on the axis of symmetry, so its x-coordinate is \(−\frac{b}{2a}\).
To find the y-coordinate of the vertex, we substitute x=\(−\frac{b}{2a}\) into the quadratic equation.
For the parabola \(y=3x^2−6x+2\) find:
- the axis of symmetry and
- the vertex.
- Answer
-
1. 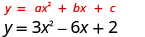
The axis of symmetry is the line x=\(−\frac{b}{2a}\) 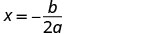
Substitute the values of a, b into the equation. 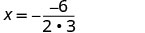
Simplify x=1 The axis of symmetry is the line x=1 2. 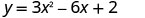
The vertex is on the line of symmetry, so its x-coordinate will be x=1 Substitute x=1 into the equation and solve for y. 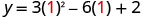
Simplify 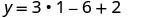
This is the y-coordinate. y=−1
The vertex is (1,−1).
For the parabola \(y=2x^2−8x+1\) find:
- the axis of symmetry and
- the vertex.
- Answer
-
- x=2
- (2,−7)
For the parabola \(y=2x^2−4x−3\) find:
- the axis of symmetry and
- the vertex.
- Answer
-
- x=1
- (1,−5)
Find the Intercepts of a Parabola
When we graphed linear equations, we often used the x- and y-intercepts to help us graph the lines. Finding the coordinates of the intercepts will help us to graph parabolas, too.
Remember, at the y-intercept the value of x is zero. So, to find the y-intercept, we substitute x=0 into the equation.
Let’s find the y-intercepts of the two parabolas shown in the figure below.
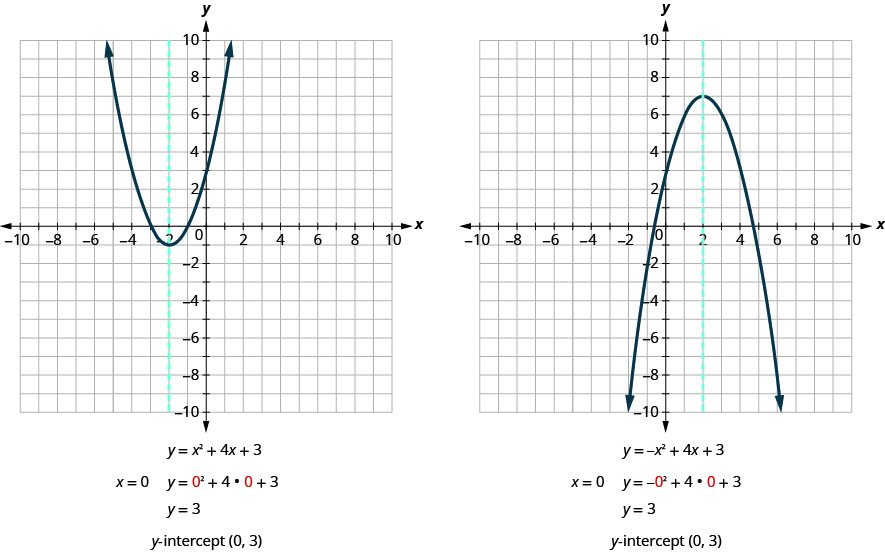
At an x-intercept, the value of y is zero. To find an x-intercept, we substitute \(y=0\) into the equation. In other words, we will need to solve the equation \(0=ax^2+bx+c\) for x.
\[\begin{array} {ll} {y=ax^2+bx+c} \\ {0=ax^2+bx+c} \\ \nonumber \end{array}\]
But solving quadratic equations like this is exactly what we have done earlier in this chapter.
We can now find the x-intercepts of the two parabolas shown in Figure.
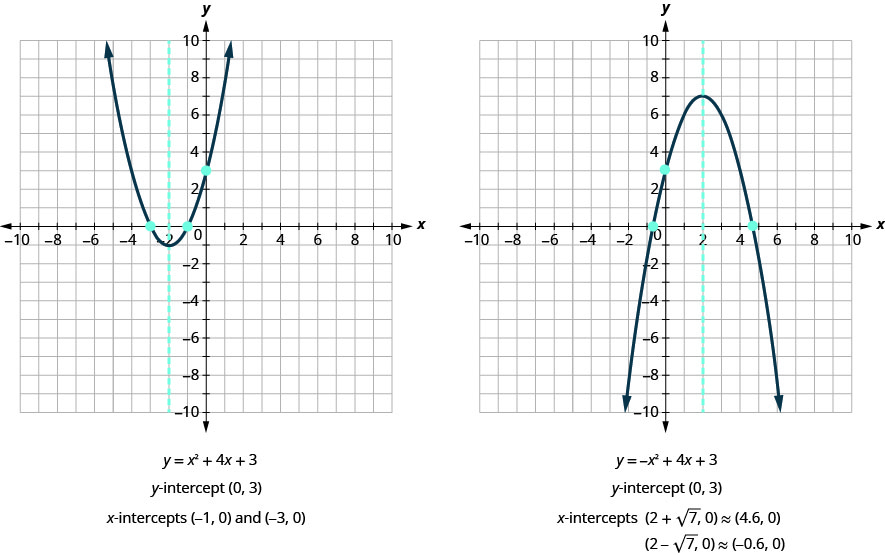
First, we will find the x-intercepts of a parabola with equation \(y=x^2+4x+3\).
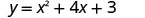 |
||
| Let y=0 | 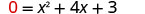 |
|
| Factor. | 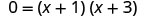 |
|
| Use the zero product property. | 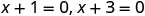 |
|
| Solve. | 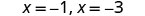 |
|
| The x intercepts are (−1,0) and (−3,0). | ||
Now, we will find the x-intercepts of the parabola with equation \(y=−x^2+4x+3\).
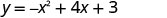 |
||
| Let y=0 | 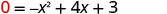 |
|
| This quadratic does not factor, so we use the Quadratic Formula. | 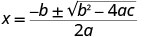 |
|
| a=−1, b=4, c=3. | 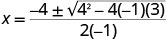 |
|
| Simplify. | 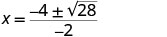 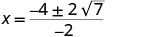 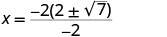 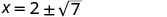 |
|
| The x intercepts are \((2+\sqrt{7},0)\) and \((2−\sqrt{7},0)\) | ||
We will use the decimal approximations of the x-intercepts, so that we can locate these points on the graph.
\[\begin{array} {l} {(2+\sqrt{7},0) \approx (4.6,0)} & {(2−\sqrt{7},0) \approx (-0.6,0)}\\ \nonumber \end{array}\]
Do these results agree with our graphs? See Figure.
To find the intercepts of a parabola with equation \(y=ax^2+bx+c\):
\[\begin{array}{ll} {\textbf{y-intercept}}& {\textbf{x-intercept}}\\ {\text{Let} x=0 \text{and solve the y}}& {\text{Let} y=0 \text{and solve the x}}\\ \nonumber \end{array}\]
Find the intercepts of the parabola \(y=x^2−2x−8\).
- Answer
-
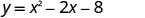
To find the y-intercept, let x=0 and solve for y. 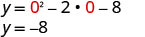
When x=0, then y=−8.
The y-intercept is the point (0,−8).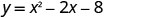
To find the x-intercept, let y=0 and solve for x. 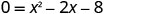
Solve by factoring. 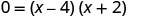
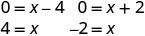
- When y=0, then x=4 or x=−2. The x-intercepts are the points (4,0) and (−2,0).
Find the intercepts of the parabola \(y=x^2+2x−8\).
- Answer
-
y:(0,−8); x:(−4,0), (2,0)
Find the intercepts of the parabola \(y=x^2−4x−12\).
- Answer
-
y:(0,−12); x:(6,0), (−2,0)
In this chapter, we have been solving quadratic equations of the form \(ax^2+bx+c=0\). We solved for xx and the results were the solutions to the equation.
We are now looking at quadratic equations in two variables of the form \(y=ax^2+bx+c\). The graphs of these equations are parabolas. The x-intercepts of the parabolas occur where y=0.
For example:
\[\begin{array}{cc} {\textbf{Quadratic equation}}&{\textbf{Quadratic equation in two variable}}\\ {}&{y=x^2−2x−15}\\ {x^2−2x−15}&{\text{Let} y=0, 0=x^2−2x−15}\\ {(x−5)(x+3)=0}&{0=(x−5)(x+3)}\\ {x−5=0, x+3=0}&{x−5=0, x+3=0}\\ {x=5, x=−3}&{x=5, x=−3}\\ {}&{(5,0) \text{and} (−3,0)}\\ {}&{\text{x-intercepts}}\\ \end{array}\]
The solutions of the quadratic equation are the x values of the x-intercepts.
Earlier, we saw that quadratic equations have 2, 1, or 0 solutions. The graphs below show examples of parabolas for these three cases. Since the solutions of the equations give the x-intercepts of the graphs, the number of x-intercepts is the same as the number of solutions.
Previously, we used the discriminant to determine the number of solutions of a quadratic equation of the form \(ax^2+bx+c=0\). Now, we can use the discriminant to tell us how many x-intercepts there are on the graph.
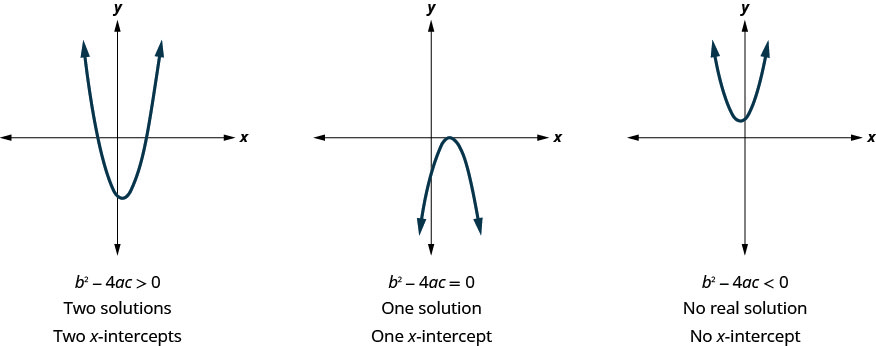
Before you start solving the quadratic equation to find the values of the x-intercepts, you may want to evaluate the discriminant so you know how many solutions to expect.
Find the intercepts of the parabola \(y=5x^2+x+4\).
- Answer
-
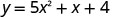
To find the y-intercept, let x=0 and solve for y. 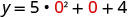

When x=0, then y=4.
The y-intercept is the point (0,4).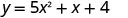
To find the x-intercept, let y=0 and solve for x. 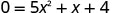
Find the value of the discriminant to predict the number of solutions and so x-intercepts. b^2−4ac
1^2−4⋅5⋅4
1−80
−79
Since the value of the discriminant is negative, there is no real solution to the equation. There are no x-intercepts.
Find the intercepts of the parabola \(y=3x^2+4x+4\).
- Answer
-
y:(0,4); x:none
Find the intercepts of the parabola \(y=x^2−4x−5\).
- Answer
-
y:(0,−5); x:(5,0)(−1,0)
Find the intercepts of the parabola \(y=4x^2−12x+9\).
- Answer
-
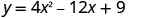
To find the y-intercept, let x=0 and solve for y. 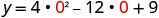

When x=0, then y=9.
The y-intercept is the point (0,9).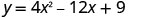
To find the x-intercept, let y=0 and solve for x. 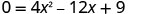
Find the value of the discriminant to predict the number of solutions and so x-intercepts. b^2−4ac
12^2−4⋅4⋅9
144−144
0
Since the value of the discriminant is 0, there is no real solution to the equation. So there is one x-intercept. Solve the equation by factoring the perfect square trinomial. 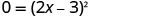
Use the Zero Product Property. 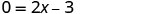
Solve for x. 

When y=0, then \(\frac{3}{2}\)=x. The x-intercept is the point \((\frac{3}{2},0)\).
Find the intercepts of the parabola \(y=−x^2−12x−36.\).
- Answer
-
y:(0,−36); x:(−6,0)
Find the intercepts of the parabola \(y=9x^2+12x+4\).
- Answer
-
y:(0,4); x:\((−\frac{2}{3},0)\)
Graph Quadratic Equations in Two Variables
Now, we have all the pieces we need in order to graph a quadratic equation in two variables. We just need to put them together. In the next example, we will see how to do this.
How To Graph a Quadratic Equation in Two Variables
Graph \(y=x2−6x+8\).
- Answer
-


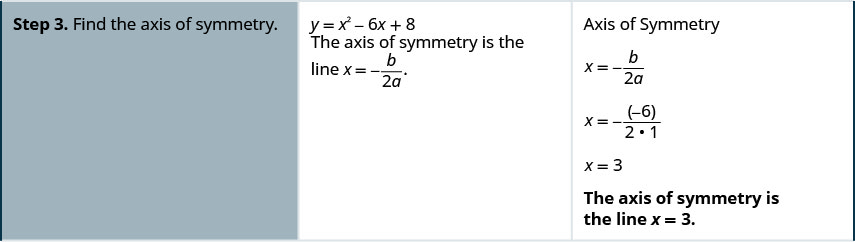




Graph the parabola \(y=x^2+2x−8\).
- Answer
-
y:(0,−8); x:(2,0),(−4,0);
axis: x=−1; vertex: (−1,−9);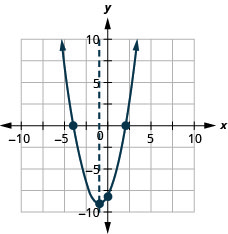
Graph the parabola \(y=x^2−8x+12\).
- Answer
-
y:(0,12); x:(2,0),(6,0);
axis: x=4; vertex:(4,−4);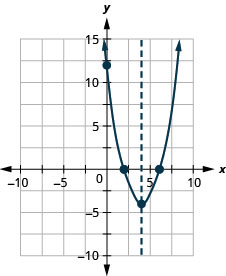
- Write the quadratic equation with yy on one side.
- Determine whether the parabola opens upward or downward.
- Find the axis of symmetry.
- Find the vertex.
- Find the y-intercept. Find the point symmetric to the y-intercept across the axis of symmetry.
- Find the x-intercepts.
- Graph the parabola.
We were able to find the x-intercepts in the last example by factoring. We find the x-intercepts in the next example by factoring, too.
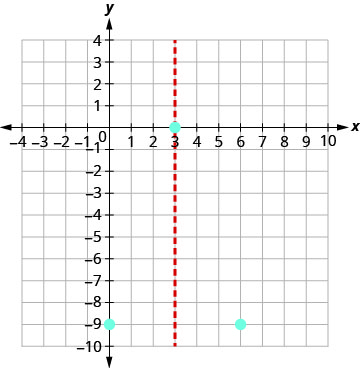
Graph \(y=−x^2+6x−9\).
- Answer
-
The equation y has on one side. 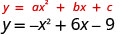
Since a is −1, the parabola opens downward.
To find the axis of symmetry, find \(x=−\frac{b}{2a}\).
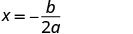
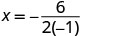

The axis of symmetry is x=3. The vertex is on the line x=3.
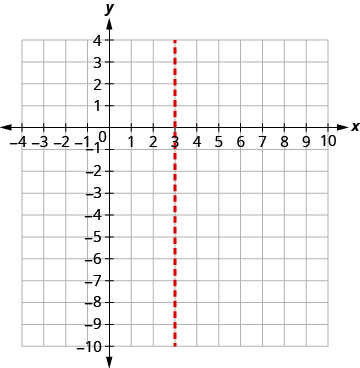
Find y when x=3.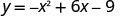
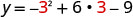
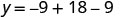

The vertex is (3,0).
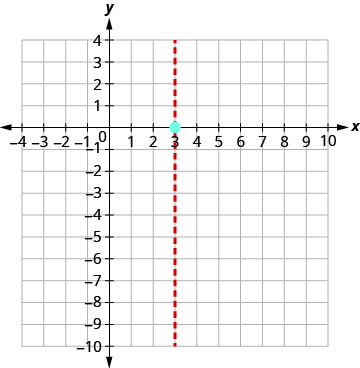
The y-intercept occurs when x=0.
Substitute x=0.
Simplify.
The point (0,−9) is three units to the left of the line of symmetry.
The point three units to the right of the line of symmetry is (6,−9).
Point symmetric to the y-intercept is (6,−9)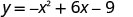
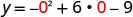

(0,−9).
The x-intercept occurs when y=0. 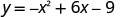
Substitute y=0. 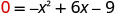
Factor the GCF. 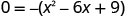
Factor the trinomial. 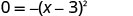
Solve for x. 
Connect the points to graph the parabola. 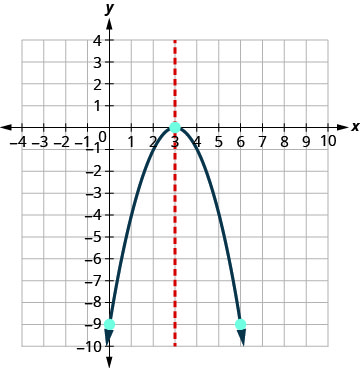
Graph the parabola \(y=−3x^2+12x−12\).
- Answer
-
y:(0,−12); x:(2,0);
axis: x=2; vertex:(2,0);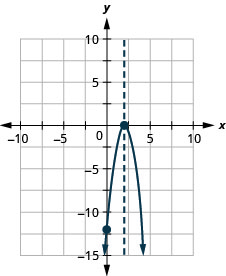
Graph the parabola \(y=25x^2+10x+1\).
- Answer
-
y:(0,1); x:(−15,0);
axis: x=−15; vertex:(−15,0);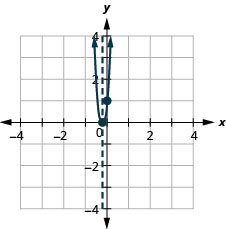
For the graph of \(y=−x^2+6x−9\) the vertex and the x-intercept were the same point. Remember how the discriminant determines the number of solutions of a quadratic equation? The discriminant of the equation \(0=−x^2+6x−9\) is 0, so there is only one solution. That means there is only one x-intercept, and it is the vertex of the parabola.
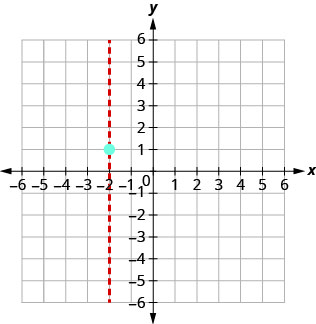
How many x-intercepts would you expect to see on the graph of \(y=x^2+4x+5\)?
Graph \(y=x^2+4x+5\).
- Answer
-
The equation has y on one side. 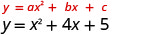
Since a is 1, the parabola opens upward. 
\(x=−\frac{b}{2a}\). 
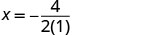

x=−2.
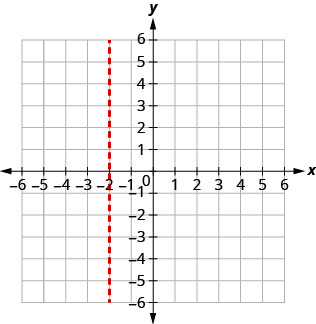
The vertex is on the line x=−2. Find y when x=−2. 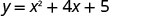
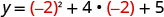
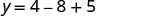

(−2,1).
The y-intercept occurs when x=0.
Substitute x=0.
Simplify.
The point (0,5) is two units to the right of the line of symmetry.
The point two units to the left of the line of symmetry is (−4,5).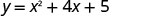
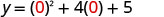

(0,5).
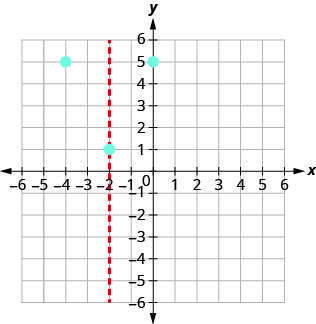
(−4,5)The x- intercept occurs when y=0. Substitute y=0.
Test the discriminant.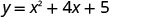
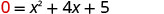
\(b^2−4ac\)
\(42−4⋅15\)
\(16−20\)
\(−4\)Since the value of the discriminant is negative, there is no solution and so no x- intercept.
Connect the points to graph the parabola. You may want to choose two more points for greater accuracy.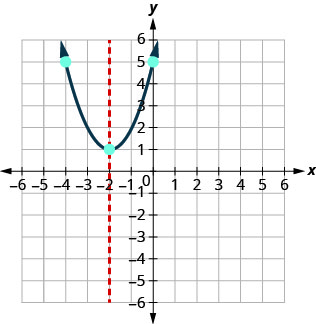
Graph the parabola \(y=2x^2−6x+5\).
- Answer
-
y:(0,5); x:none;
axis: \(x=\frac{3}{2}\); vertex:\((\frac{3}{2},\frac{1}{2})\);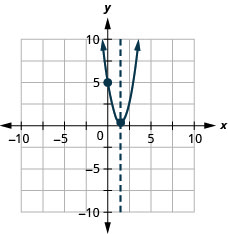
Graph the parabola \(y=−2x^2−1\).
- Answer
-
y:(0,−1); x:none;
axis: x=0; vertex:(0,−1);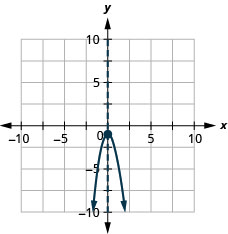
Finding the y-intercept by substituting x=0 into the equation is easy, isn’t it? But we needed to use the Quadratic Formula to find the x-intercepts in Example. We will use the Quadratic Formula again in the next example.
Graph \(y=2x^2−4x−3\).
- Answer
-

The equation y has one side.
Since a is 2, the parabola opens upward.
To find the axis of symmetry, find\(x=−\frac{b}{2a}\) 


The vertex is x=1The vertex on the line x=1. 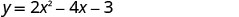
Find y when x=1 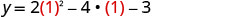


(1,−5)The y-intercept occurs when x=0. 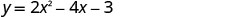
Substitute x=0. 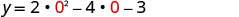
Simplify. 
The y-intercept is (0,−3)
The point (0,−3) is one unit to the left of the line of symmetry.
The point one unit to the right of the line of symmetry is (2,−3)Point symmetric to the y-intercept is (2,−3). The x-intercept occurs when y=0 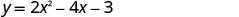
Substitute y=0 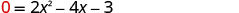
Use the Quadratic Formula. 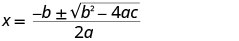
Substitute in the values of a, b, c. 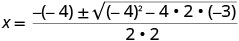
Simplify. 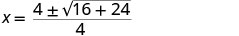
Simplify inside the radical. 
Simplify the radical. 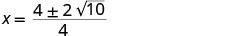
Factor the GCF. 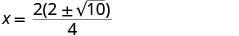
Remove common factors. 
Write as two equations. 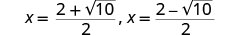
Approximate the values. 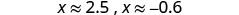
The approximate values of the x-intercepts are (2.5,0) and (−0.6,0). Graph the parabola using the points found. 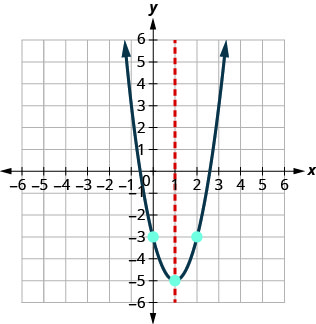
Graph the parabola \(y=5x^2+10x+3\).
- Answer
-
y:(0,3); x:(−1.6,0),(−0.4,0);
axis: x=−1; vertex:(−1,−2);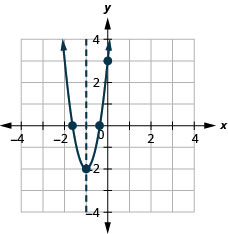
Graph the parabola \(y=−3x^2−6x+5\).
- Answer
-
y:(0,5); x:(0.6,0),(−2.6,0);
axis: x=−1; vertex:(−1,8);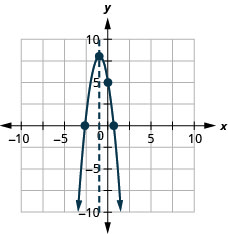
Solve Maximum and Minimum Applications
Knowing that the vertex of a parabola is the lowest or highest point of the parabola gives us an easy way to determine the minimum or maximum value of a quadratic equation. The y-coordinate of the vertex is the minimum y-value of a parabola that opens upward. It is the maximum y-value of a parabola that opens downward. See Figure.
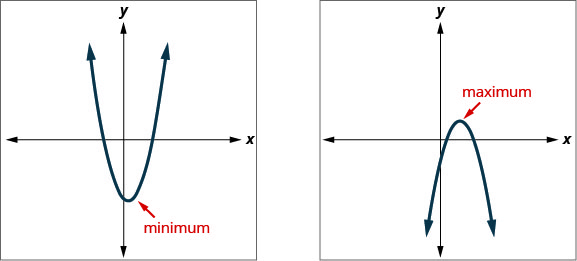
The y-coordinate of the vertex of the graph of a quadratic equation is the
- minimum value of the quadratic equation if the parabola opens upward.
- maximum value of the quadratic equation if the parabola opens downward.
Find the minimum value of the quadratic equation \(y=x^2+2x−8\).
- Answer
-
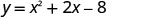
Since a is positive, the parabola opens upward. The quadratic equation has a minimum. Find the axis of symmetry. 
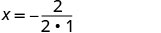

x=−1The vertex is on the line x=−1. 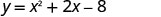
Find y when x=−1. 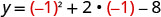
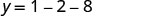

(−1,−9)Since the parabola has a minimum, the y-coordinate of the vertex is the minimum y-value of the quadratic equation. The minimum value of the quadratic is −9 and it occurs when x=−1. Show the graph to verify the result. 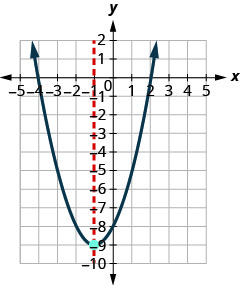
Find the maximum or minimum value of the quadratic equation \(y=x^2−8x+12\).
- Answer
-
The minimum value is −4 when x=4.
Find the maximum or minimum value of the quadratic equation \(y=−4x^2+16x−11\).
- Answer
-
The maximum value is 5 when x=2.
We have used the formula
\[\begin{array} {l} {h=−16t^2+v_{0}t+h_{0}}\\ \nonumber \end{array}\]
to calculate the height in feet, h, of an object shot upwards into the air with initial velocity, \(v_{0}\), after t seconds.
This formula is a quadratic equation in the variable tt, so its graph is a parabola. By solving for the coordinates of the vertex, we can find how long it will take the object to reach its maximum height. Then, we can calculate the maximum height.
The quadratic equation \(h=−16t^2+v_{0}t+h_{0}\) models the height of a volleyball hit straight upwards with velocity 176 feet per second from a height of 4 feet.
- How many seconds will it take the volleyball to reach its maximum height?
- Find the maximum height of the volleyball.
- Answer
-
\(h=−16t^2+176t+4\)
Since a is negative, the parabola opens downward.
The quadratic equation has a maximum.
1.
\[\begin{array} {ll} {}&{t=−\frac{b}{2a}}\\ {\text{Find the axis of symmetry.}}& {t=−\frac{176}{2(−16)}}\\ {}&{t=5.5}\\ {}&{\text{The axis of symmetry is} t = 5.5}\\ {\text{The vertex is on the line} t=5.5}& {\text{The maximum occurs when} t =5.5 \text{seconds.}}\\ \nonumber \end{array}\]2.
Find h when t=5.5. 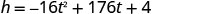
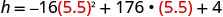
Use a calculator to simplify. 
The vertex is (5.5,488) Since the parabola has a maximum, the h-coordinate of the vertex is the maximum y-value of the quadratic equation. The maximum value of the quadratic is 488 feet and it occurs when t=5.5 seconds.
The quadratic equation \(h=−16t^2+128t+32\) is used to find the height of a stone thrown upward from a height of 32 feet at a rate of 128 ft/sec. How long will it take for the stone to reach its maximum height? What is the maximum height? Round answers to the nearest tenth.
- Answer
-
It will take 4 seconds to reach the maximum height of 288 feet.
A toy rocket shot upward from the ground at a rate of 208 ft/sec has the quadratic equation of \(h=−16t^2+208t\). When will the rocket reach its maximum height? What will be the maximum height? Round answers to the nearest tenth.
- Answer
-
It will take 6.5 seconds to reach the maximum height of 676 feet.
- Graphing Quadratic Functions
- How do you graph a quadratic function?
- Graphing Quadratic Equations
Key Concepts
- The graph of every quadratic equation is a parabola.
- Parabola Orientation For the quadratic equation \(y=ax^2+bx+c\), if
- a>0, the parabola opens upward.
- a<0, the parabola opens downward.
- Axis of Symmetry and Vertex of a Parabola For a parabola with equation \(y=ax^2+bx+c\):
- The axis of symmetry of a parabola is the line \(x=−\frac{b}{2a}\).
- The vertex is on the axis of symmetry, so its x-coordinate is \(−\frac{b}{2a}\).
- To find the y-coordinate of the vertex we substitute \(x=−\frac{b}{2a}\) into the quadratic equation.
- Find the Intercepts of a Parabola To find the intercepts of a parabola with equation \(y=ax^2+bx+c\):
\[\begin{array} {ll} {\textbf{y-intercept}}&{\textbf{x-intercepts}}\\ {\text{Let} x=0 \text{and solve for y}}&{\text{Let} y=0 \text{and solve for x}}\\ \nonumber \end{array}\] - To Graph a Quadratic Equation in Two Variables
- Write the quadratic equation with yy on one side.
- Determine whether the parabola opens upward or downward.
- Find the axis of symmetry.
- Find the vertex.
- Find the y-intercept. Find the point symmetric to the y-intercept across the axis of symmetry.
- Find the x-intercepts.
- Graph the parabola.
- Minimum or Maximum Values of a Quadratic Equation
- The y-coordinate of the vertex of the graph of a quadratic equation is the
- minimum value of the quadratic equation if the parabola opens upward.
- maximum value of the quadratic equation if the parabola opens downward.
Glossary
- axis of symmetry
- The axis of symmetry is the vertical line passing through the middle of the parabola \(y=ax^2+bx+c\).
- parabola
- The graph of a quadratic equation in two variables is a parabola.
- quadratic equation in two variables
- A quadratic equation in two variables, where a, b, and c are real numbers and \(a \ge 0\) is an equation of the form \(y=ax^2+bx+c\).
- vertex
- The point on the parabola that is on the axis of symmetry is called the vertex of the parabola; it is the lowest or highest point on the parabola, depending on whether the parabola opens upwards or downwards.
- x-intercepts of a parabola
- The x-intercepts are the points on the parabola where \(y=0\).
- y-intercept of a parabola
- The y-intercept is the point on the parabola where \(x=0\).


