Chapter 1 Review Exercises

Last updated
Save as PDF

Page ID: 5749

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Chapter Review Exercises

Use the Language of Algebra

Identify Multiples and Factors

1. Use the divisibility tests to determine whether 180 is divisible by 2, by 3, by 5, by 6, and by 10.

Answer: Divisible by $2,3,5,6$

2. Find the prime factorization of 252.

3. Find the least common multiple of 24 and 40.

Answer: 120

In the following exercises, simplify each expression.

4. $24÷3+4(5−2)$

5. $7+3[6−4(5−4)]−3^2$

Answer: 4

Evaluate an Expression

In the following exercises, evaluate the following expressions.

6. When $x=4$, ⓐ $x^3$ ⓑ $5x$ ⓒ $2x^2−5x+3$

7. $2x^2−4xy−3y^2$ when $x=3$ and $y=1$

Answer: 3

Simplify Expressions by Combining Like Terms

In the following exercises, simplify the following expressions by combining like terms.

8. $12y+7+2y−5$

9. $14x^2−9x+11−8x^2+8x−6$

Answer: $6x^2−x+5$

Translate an English Phrase to an Algebraic Expression

In the following exercises, translate the phrases into algebraic expressions.

10. ⓐ the sum of $4ab^2$ and $7a3b24ab^2$ and $7a^3b^2$

ⓑ the product of $6y^2$ and $3y$

ⓓ $5y$ less than $8y^2$

11. ⓐ eleven times the difference of $y$ and two

ⓑ the difference of eleven times $y$ and two

Answer: ⓐ $11(y−2)$
ⓑ $11y−2$

12. Dushko has nickels and pennies in his pocket. The number of pennies is four less than five the number of nickels. Let nn represent the number of nickels. Write an expression for the number of pennies.

Integers

Simplify Expressions with Absolute Value

In the following exercise, fill in $<,>,$ or $=$ for each of the following pairs of numbers.

13. ⓐ $−|7| \_\_\_−|−7|$

ⓑ $−8 \_\_\_−|−8|$

ⓓ $|−12| \_\_\_−(−12)$

Answer: ⓐ $=$
ⓑ $=$
ⓒ $>$
ⓓ $=$

In the following exercises, simplify.

14. $9−|3(4−8)|$

15. $12−3|1−4(4−2)|$

Answer: $−9$

Add and Subtract Integers

In the following exercises, simplify each expression.

16. $−12+(−8)+7$

17. ⓐ $15−7$

ⓑ $−15−(−7)$

ⓓ $15−(−7)$

Answer: ⓐ $8$
ⓑ $−8$
ⓒ $−22$
ⓓ $22$

18. $−11−(−12)+5$

19. ⓐ $23−(−17)$ ⓑ $23+17$

Answer: ⓐ 40 ⓑ 40

20. $−(7−11)−(3−5)$

Multiply and Divide Integers

In the following exercise, multiply or divide.

21. ⓐ $−27÷9$ ⓑ $120÷(−8)$ ⓒ $4(−14)$ ⓓ $−1(−17)$

Answer: ⓐ $−3$ ⓑ $−15$ ⓒ $−56$ ⓓ $17$

Simplify and Evaluate Expressions with Integers

In the following exercises, simplify each expression.

22. ⓐ $(−7)^3$ ⓑ $−7^3$

23. $(7−11)(6−13)$

Answer: 16

24. $63÷(−9)+(−36)÷(−4)$

25. $6−3|4(1−2)−(7−5)|$

Answer: $−12$

26. $(−2)^4−24÷(13−5)$

For the following exercises, evaluate each expression.

27. $(y+z)^2$ when $y=−4$ and $z=7$

Answer: 9

28. $3x^2−2xy+4y^2$ when $x=−2$ and $y=−3$

Translate English Phrases to Algebraic Expressions

In the following exercises, translate to an algebraic expression and simplify if possible.

29. the sum of $−4$ and $−9$, increased by $23$

Answer: $(−4+(−9))+23;10$

30. ⓐ the difference of 17 and −8 ⓑ subtract 17 from −25

Use Integers in Applications

In the following exercise, solve.

31. Temperature On July 10, the high temperature in Phoenix, Arizona, was 109°, and the high temperature in Juneau, Alaska, was 63°. What was the difference between the temperature in Palm Springs and the temperature in Whitefield?

Answer: $46°$

Fractions

Simplify Fractions

In the following exercises, simplify.

32. $\dfrac{204}{228}$

33. $−\dfrac{270x^3}{198y^2}$

Answer: $−\dfrac{15x^3}{11y^2}$

Multiply and Divide Fractions

In the following exercises, perform the indicated operation.

34. $\left(−\dfrac{14}{15}\right)\left(\dfrac{10}{21}\right)$

35. $\dfrac{6x}{25}÷\dfrac{9y}{20}$

Answer: $\dfrac{8x}{15y}$

36. $\dfrac{−\frac{4}{9}}{\dfrac{8}{21}}$

Add and Subtract Fractions

In the following exercises, perform the indicated operation.

37. $\dfrac{5}{18}+\dfrac{7}{12}$

Answer: $\dfrac{31}{36}$

38. $\dfrac{11}{36}−\dfrac{15}{48}$

39. ⓐ $\dfrac{5}{8}+\dfrac{3}{4}$ ⓑ $\dfrac{5}{8}÷\dfrac{3}{4}$

Answer: ⓐ $\dfrac{11}{8}$ ⓑ $\dfrac{5}{6}$

40. ⓐ $−\dfrac{3y}{10}−\dfrac{5}{6}$ ⓑ $−\dfrac{3y}{10}·\dfrac{5}{6}$

Use the Order of Operations to Simplify Fractions

In the following exercises, simplify.

41. $\dfrac{4·3−2·5}{−6·3+2·3}$

Answer: $−\dfrac{1}{6}$

42. $\dfrac{4(7−3)−2(4−9)}{−3(4+2)+7(3−6)}$

43. $\dfrac{4^3−4^2}{(\dfrac{4}{5})^2}$

Answer: 75

Evaluate Variable Expressions with Fractions

In the following exercises, evaluate.

44. $4x^2y^2$ when $x=\dfrac{2}{3}$ and $y=−\dfrac{3}{4}$

45. $\dfrac{a+b}{a−b}$ when $a=−4$ and $b=6$

Answer: $−15$

Decimals

Round Decimals

46. Round $6.738$ to the nearest ⓐ hundredth ⓑ tenth ⓒ whole number.

Add and Subtract Decimals

In the following exercises, perform the indicated operation.

47. $−23.67+29.84$

Answer: $6.17$

48. $54.3−100$

49. $79.38−(−17.598)$

Answer: $96.978$

Multiply and Divide Decimals

In the following exercises, perform the indicated operation.

50. $(−2.8)(3.97)$

51. $(−8.43)(−57.91)$

Answer: 488.1813

52. $(53.48)(10)$

53. $(0.563)(100)$

Answer: $56.3$

54. $ \$ 118.35÷2.6$

55. $1.84÷(−0.8)$

Answer: $−23$

Convert Decimals, Fractions and Percents

In the following exercises, write each decimal as a fraction.

56. $\dfrac{13}{20}$

57. $−\dfrac{240}{25}$

Answer: $−9.6$

In the following exercises, convert each fraction to a decimal.

58. $−\dfrac{5}{8}$

59. $\dfrac{14}{11}$

Answer: $1.\overline{27}$

In the following exercises, convert each decimal to a percent.

60. $2.43$

61. $0.0475$

Answer: $4.75 \% $

Simplify Expressions with Square Roots

In the following exercises, simplify.

62. $\sqrt{289}$

63. $\sqrt{−121}$

Answer: no real number

Identify Integers, Rational Numbers, Irrational Numbers, and Real Numbers

In the following exercise, list the ⓐ whole numbers ⓑ integers ⓒ rational numbers ⓓ irrational numbers ⓔ real numbers for each set of numbers

64. $−8,0,1.95286...,\dfrac{12}{5},\sqrt{36},9$

Locate Fractions and Decimals on the Number Line

In the following exercises, locate the numbers on a number line.

65. $\dfrac{3}{4},−\dfrac{3}{4},1\dfrac{1}{3},−1\dfrac{2}{3},\dfrac{7}{2},−\dfrac{5}{2}$

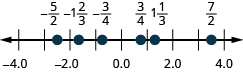
Answer: $Figure shows a number line with numbers ranging from minus 4 to 4. Some values are highlighted.$

66. ⓐ $3.2$ ⓑ $−1.35$

Properties of Real Numbers

Use the Commutative and Associative Properties

In the following exercises, simplify.

67. $\dfrac{5}{8}x+\dfrac{5}{12}y+\dfrac{1}{8}x+\dfrac{7}{12}y$

Answer: $\dfrac{3}{4}x+y$

68. $−32·9·\dfrac{5}{8}$

69. $\left(\dfrac{11}{15}+\dfrac{3}{8}\right)+\dfrac{5}{8}$

Answer: $1\dfrac{11}{15}$

Use the Properties of Identity, Inverse and Zero

In the following exercises, simplify.

70. $\dfrac{4}{7}+\dfrac{8}{15}+\left(−\dfrac{4}{7}\right)$

71. $\dfrac{13}{15}·\dfrac{9}{17}·\dfrac{15}{13}$

Answer: $\dfrac{9}{17}$

72. $\dfrac{0}{x−3},x\neq 3$

73. $\dfrac{5x−7}{0},5x−7\neq 0$

Answer: undefined

Simplify Expressions Using the Distributive Property

In the following exercises, simplify using the Distributive Property.

74. $8(a−4)$

75. $12\left(\dfrac{2}{3}b+\dfrac{5}{6}\right)$

Answer: $8b+10$

76. $18·\dfrac{5}{6}(2x−5)$

77. $(x−5)p$

Answer: $xp−5p$

78. $−4(y−3)$

79. $12−6(x+3)$

Answer: $−6x−6$

80. $6(3x−4)−(−5)$

81. $5(2y+3)−(4y−1)$

Answer: $y+16$

Practice Test

1. Find the prime factorization of $756$.

2. Combine like terms: $5n+8+2n−1$

Answer: $7n+7$

3. Evaluate when $x=−2$ and $y=3: \dfrac{|3x−4y|}{6}$

4. Translate to an algebraic expression and simplify:

ⓐ eleven less than negative eight

ⓑ the difference of $−8$ and $−3$, increased by 5

Answer: $−8−11 = −19$
$(−8−(−3))+5 = 0$

5. Dushko has nickels and pennies in his pocket. The number of pennies is seven less than four times the number of nickels. Let nn represent the number of nickels. Write an expression for the number of pennies.

6. Round $28.1458$ to the nearest

ⓐ hundredth ⓑ thousandth

Answer: ⓐ $28.15$ ⓑ $28.146$

7. Convert

ⓐ $\dfrac{5}{11}$ to a decimal ⓑ $1.15$ to a percent

8. Locate $\dfrac{3}{5},2.8,and−\dfrac{5}{2}$ on a number line.

Answer: $alt$

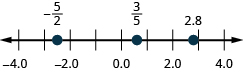
In the following exercises, simplify each expression.

9. $8+3[6−3(5−2)]−4^2$

10. $−(4−9)−(9−5)$

Answer: 1

11. $56÷(−8)+(−27)÷(−3)$

12. $16−2|3(1−4)−(8−5)|$

Answer: $−8$

13. $−5+2(−3)^2−9$

14. $\dfrac{180}{204}$

Answer: $\dfrac{15}{17}$

15. $−\dfrac{7}{18}+\dfrac{5}{12}$

16. $\dfrac{4}{5}÷(−\dfrac{12}{25})$

Answer: $−\dfrac{5}{3}$

17. $\dfrac{9−3·9}{15−9}$

18. $\dfrac{4(−3+2(3−6))}{3(11−3(2+3))}$

Answer: $3$

19. $\dfrac{5}{13}⋅\dfrac{4}{7}⋅\dfrac{13}{5}$

20. $\dfrac{−\dfrac{5}{9}}{\dfrac{10}{21}}$

Answer: $−\dfrac{7}{6}$

21. $−4.8+(−6.7)$

22. $34.6−100$

Answer: $−65.4$

23. $−12.04⋅(4.2)$

24. $−8÷0.05$

Answer: 160

25. $−\sqrt{121}$

26. $(\dfrac{8}{13}+\dfrac{5}{7})+\dfrac{2}{7}$

Answer: $1\dfrac{8}{13}$

27. $5x+(−8y)−6x+3y$

28. ⓐ $\dfrac{0}{9}$ ⓑ $\dfrac{11}{0}$

Answer: ⓐ 0 ⓑ undefined

29. $−3(8x−5)$

30. $6(3y−1)−(5y−3)$

Answer: $13y−3$

Search

Text Color

Text Size

Margin Size

Font Type