3.6: Relations and Functions

Last updated
Save as PDF

Page ID: 5135

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

By the end of this section, you will be able to:

Find the domain and range of a relation
Determine if a relation is a function
Find the value of a function

Before you get started, take this readiness quiz.

Evaluate $3x−5$ when $x=−2$.
If you missed this problem, review [link].
Evaluate $2x^2−x−3$ when $x=a$.
If you missed this problem, review [link].
Simplify: $7x−1−4x+5$.
If you missed this problem, review [link].

Find the Domain and Range of a Relation

As we go about our daily lives, we have many data items or quantities that are paired to our names. Our social security number, student ID number, email address, phone number and our birthday are matched to our name. There is a relationship between our name and each of those items.

When your professor gets her class roster, the names of all the students in the class are listed in one column and then the student ID number is likely to be in the next column. If we think of the correspondence as a set of ordered pairs, where the first element is a student name and the second element is that student’s ID number, we call this a relation.

\[(\text{Student name}, \text{ Student ID #})\nonumber \]

The set of all the names of the students in the class is called the domain of the relation and the set of all student ID numbers paired with these students is the range of the relation.

There are many similar situations where one variable is paired or matched with another. The set of ordered pairs that records this matching is a relation.

Definition: Relation

A relation is any set of ordered pairs, $(x,y)$. All the x-values in the ordered pairs together make up the domain. All the y-values in the ordered pairs together make up the range.

Example $\PageIndex{1}$

For the relation ${(1,1),(2,4),(3,9),(4,16),(5,25)}$:

Find the domain of the relation.
Find the range of the relation.

Answer: \[\begin{array} {ll} {} &{ {\{(1,1), (2,4), (3,9), (4,16), (5,25) }\} } \\ {ⓐ\text{ The domain is the set of all x-values of the relation.}} &{ {\{1,2,3,4,5}\} } \\ {ⓑ\text{ The range is the set of all y-values of the relation.}} &{ {\{1,4,9,16,25}\} } \\ \nonumber \end{array}\]

Example $\PageIndex{2}$

For the relation ${\{(1,1),(2,8),(3,27),(4,64),(5,125)}\}$:

Find the domain of the relation.
Find the range of the relation.

Answer a: ${\{1,2,3,4,5}\}$
Answer b: ${\{1,8,27,64,125}\}$

Example $\PageIndex{3}$

For the relation ${\{(1,3),(2,6),(3,9),(4,12),(5,15)}\}$:

Find the domain of the relation.
Find the range of the relation.

Answer a: ${\{1,2,3,4,5}\}$
Answer b: ${\{3,6,9,12,15}\}$

MAPPING

A mapping is sometimes used to show a relation. The arrows show the pairing of the elements of the domain with the elements of the range.

Example $\PageIndex{4}$

Use the mapping of the relation shown to

list the ordered pairs of the relation,
find the domain of the relation, and
find the range of the relation.

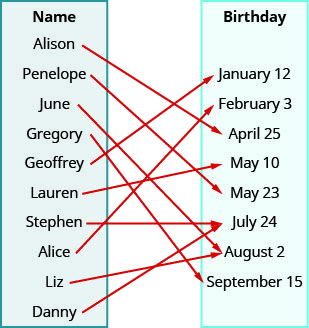
$This figure shows two table that each have one column. The table on the left has the header “Name” and lists the names “Alison”, “Penelope”, “June”, “Gregory”, “Geoffrey”, “Lauren”, “Stephen”, “Alice”, “Liz”, “Danny”. The table on the right has the header “Birthday” and lists the dates “January 12”, “February 3”, “April 25”, “May 10”, “May 23”, “July 24”, “August 2”, and “September 15”. There is one arrow for each name in the Name table that starts at the name and points toward a date in the Birthday table. While most dates have only one arrow pointing to them, there are two arrows pointing to July 24: one from Stephen and one from Liz.$

Answer

ⓐ The arrow shows the matching of the person to their birthday. We create ordered pairs with the person’s name as the x-value and their birthday as the y-value.

{(Alison, April 25), (Penelope, May 23), (June, August 2), (Gregory, September 15), (Geoffrey, January 12), (Lauren, May 10), (Stephen, July 24), (Alice, February 3), (Liz, August 2), (Danny, July 24)}

ⓑ The domain is the set of all x-values of the relation.

{Alison, Penelope, June, Gregory, Geoffrey, Lauren, Stephen, Alice, Liz, Danny}

{January 12, February 3, April 25, May 10, May 23, July 24, August 2, September 15}

Example $\PageIndex{5}$

Use the mapping of the relation shown to

list the ordered pairs of the relation
find the domain of the relation
find the range of the relation.

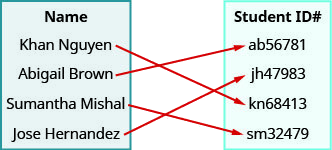
$This figure shows two table that each have one column. The table on the left has the header “Name” and lists the names “Khanh Nguyen”, “Abigail Brown”, “Sumantha Mishal”, and “Jose Hern and ez”. The table on the right has the header “Student ID #” and lists the codes “a b 56781”, “j h 47983”, “k n 68413”, and “s m 32479”. There is one arrow for each name in the Name table that starts at the name and points toward a code in the student ID table. The first arrow goes from Khanh Nguyen to k n 68413. The second arrow goes from Abigail Brown to a b 56781. The third arrow goes from Sumantha Mishal to s m 32479. The fourth arrow goes from Jose Hern and ez to j h 47983.$

Answer

ⓐ (Khanh Nguyen, kn68413), (Abigail Brown, ab56781), (Sumantha Mishal, sm32479), (Jose Hern and ez, jh47983)

ⓑ {Khanh Nguyen, Abigail Brown, Sumantha Mishal, Jose Hern and ez}

Example $\PageIndex{6}$

Use the mapping of the relation shown to

list the ordered pairs of the relation
find the domain of the relation
find the range of the relation.

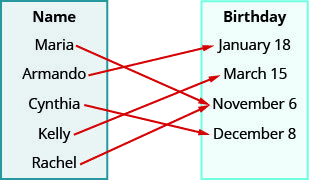
$This figure shows two table that each have one column. The table on the left has the header “Name” and lists the names “Maria”, “Arm and o”, “Cynthia”, “Kelly”, and “Rachel”. The table on the right has the header “Birthday” and lists the dates “January 18”, “March 15”, “November 6”, and “December 8”. There is one arrow for each name in the Name table that starts at the name and points toward a date in the Birthday table. The first arrow goes from Maria to November 6. The second arrow goes from Arm and o to a January 18. The third arrow goes from Cynthia to December 8. The fourth arrow goes from Kelly to March 15. The fifth arrow goes from Rachel to November 6.$

Answer

ⓐ (Maria, November 6), (Arm and o, January 18), (Cynthia, December 8), (Kelly, March 15), (Rachel, November 6)

ⓑ {Maria, Arm and o, Cynthia, Kelly, Rachel}

ⓒ{November 6, January 18, December 8, March 15}

A graph is yet another way that a relation can be represented. The set of ordered pairs of all the points plotted is the relation. The set of all x-coordinates is the domain of the relation and the set of all y-coordinates is the range. Generally we write the numbers in ascending order for both the domain and range.

Example $\PageIndex{7}$

Use the graph of the relation to

list the ordered pairs of the relation
find the domain of the relation
find the range of the relation.

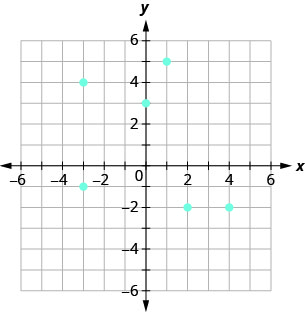
$The figure shows the graph of some points on the x y-coordinate plane. The x and y-axes run from negative 6 to 6. The points (negative 3, 4), (negative 3, negative 1), (0, 3), (1, 5), (2, negative 2), and (4, negative 2).$

Answer

ⓐ The ordered pairs of the relation are: \[{\{(1,5),(−3,−1),(4,−2),(0,3),(2,−2),(−3,4)}\}.\nonumber\]

ⓑ The domain is the set of all x-values of the relation: $\quad {\{−3,0,1,2,4}\}$.

Notice that while $−3$ repeats, it is only listed once.

Notice that while $−2$ repeats, it is only listed once.

Example $\PageIndex{8}$

Use the graph of the relation to

list the ordered pairs of the relation
find the domain of the relation
find the range of the relation.

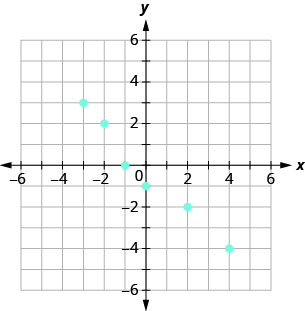
$The figure shows the graph of some points on the x y-coordinate plane. The x and y-axes run from negative 6 to 6. The points (negative 3, 3), (negative 2, 2), (negative 1, 0), (0, negative 1), (2, negative 2), and (4, negative 4).$

Answer

a. $(−3,3),(−2,2),(−1,0),$, $(0,−1),(2,−2),(4,−4)$

b. ${\{−3,−2,−1,0,2,4}\}$

c. ${\{3,2,0,−1,−2,−4}\}$

Example $\PageIndex{9}$

Use the graph of the relation to

list the ordered pairs of the relation
find the domain of the relation
find the range of the relation.

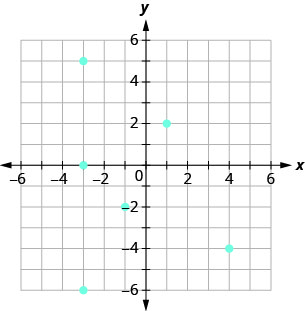
$The figure shows the graph of some points on the x y-coordinate plane. The x and y-axes run from negative 6 to 6. The points (negative 3, 5), (negative 3, 0), (negative 3, negative 6), (negative 1, negative 2), (1, 2), and (4, negative 4).$

Answer: ⓐ $(−3,0),(−3,5),(−3,−6),$
$(−1,−2),(1,2),(4,−4)$
ⓑ ${\{−3,−1,1,4}\}$
ⓒ ${\{−6,0,5,−2,2,−4}\}$

Determine if a Relation is a Function

A special type of relation, called a function, occurs extensively in mathematics. A function is a relation that assigns to each element in its domain exactly one element in the range. For each ordered pair in the relation, each x-value is matched with only one y-value.

Definition: Function

A function is a relation that assigns to each element in its domain exactly one element in the range.

The birthday example from Example helps us understand this definition. Every person has a birthday but no one has two birthdays. It is okay for two people to share a birthday. It is okay that Danny and Stephen share July 24^th as their birthday and that June and Liz share August 2^nd. Since each person has exactly one birthday, the relation in Example is a function.

The relation shown by the graph in Example includes the ordered pairs $(−3,−1)$ and $(−3,4)$. Is that okay in a function? No, as this is like one person having two different birthdays.

Example $\PageIndex{10}$

Use the set of ordered pairs to (i) determine whether the relation is a function (ii) find the domain of the relation (iii) find the range of the relation.

${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$
${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

Answer

ⓐ ${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$

(i) Each x-value is matched with only one y-value. So this relation is a function.

(ii) The domain is the set of all x-values in the relation.
The domain is: ${\{−3,−2,−1,0,1,2,3}\}$.

(iii) The range is the set of all y-values in the relation. Notice we do not list range values twice.
The range is: ${\{27,8,1,0}\}$.

ⓑ ${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

(i) The x-value 9 is matched with two y-values, both 3 and $−3$. So this relation is not a function.

(ii) The domain is the set of all x-values in the relation. Notice we do not list domain values twice.
The domain is: ${\{0,1,2,4,9}\}$.

(iii) The range is the set of all y-values in the relation.
The range is: ${\{−3,−2,−1,0,1,2,3}\}$.

Example $\PageIndex{11}$

Use the set of ordered pairs to (i) determine whether the relation is a function (ii) find the domain of the relation (iii) find the range of the function.

${\{(−3,−6),(−2,−4),(−1,−2),(0,0),(1,2),(2,4),(3,6)}\}$
${\{(8,−4),(4,−2),(2,−1),(0,0),(2,1),(4,2),(8,4)}\}$

Answer: ⓐ Yes; ${\{−3,−2,−1,0,1,2,3}\}$;
${\{−6,−4,−2,0,2,4,6}\}$
ⓑ No; ${\{0,2,4,8}\}$;
${\{−4,−2,−1,0,1,2,4}\}$

Example $\PageIndex{12}$

Use the set of ordered pairs to (i) determine whether the relation is a function (ii) find the domain of the relation (iii) find the range of the relation.

${\{(27,−3),(8,−2),(1,−1),(0,0),(1,1),(8,2),(27,3)}\}$
${\{(7,−3),(−5,−4),(8,−0),(0,0),(−6,4),(−2,2),(−1,3)}\}$

Answer: ⓐ No; ${\{0,1,8,27}\}$;
${\{−3,−2,−1,0,2,2,3}\}$
ⓑ Yes; ${\{7,−5,8,0,−6,−2,−1}\}$;
${\{−3,−4,0,4,2,3}\}$

Example $\PageIndex{13}$

Use the mapping to

determine whether the relation is a function
find the domain of the relation
find the range of the relation.

NAME	PHONE
Lydia	321-549-3327 427-658-2314
Eugene	321-964-7324
Janet	684-358-7961
Rick
Marty	684-369-7231 798-367-8541

Answer

ⓐ Both Lydia and Marty have two phone numbers. So each x-value is not matched with only one y-value. So this relation is not a function.

ⓑ The domain is the set of all x-values in the relation. The domain is: {Lydia, Eugene, Janet, Rick, Marty}

${\{321-549-3327, 427-658-2314, 321-964-7324, 684-358-7961, 684-369-7231, 798-367-8541}\}$

Example $\PageIndex{14}$

Use the mapping to ⓐ determine whether the relation is a function ⓑ find the domain of the relation ⓒ find the range of the relation.

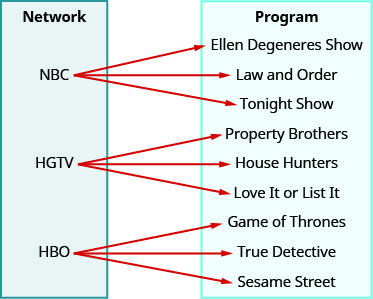
$This figure shows two table that each have one column. The table on the left has the header “Network” and lists the television stations “NBC”, “HGTV”, and “HBO”. The table on the right has the header “Program” and lists the television shows “Ellen Degeneres Show”, “Law and Order”, “Tonight Show”, “Property Brothers”, “House Hunters”, “Love it or List it”, “Game of Thrones”, “True Detective”, and “Sesame Street”. There are arrows that start at a network in the first table and point toward a program in the second table. The first arrow goes from NBC to Ellen Degeneres Show. The second arrow goes from NBC to Law and Order. The third arrow goes from NBC to Tonight Show. The fourth arrow goes from HGTV to Property Brothers. The fifth arrow goes from HGTV to House Hunters. The sixth arrow goes from HGTV to Love it or List it. The seventh arrow goes from HBO to Game of Thrones. The eighth arrow goes from HBO to True Detective. The ninth arrow goes from HBO to Sesame Street.$

Answer: ⓐ no ⓑ {NBC, HGTV, HBO} ⓒ {Ellen Degeneres Show, Law and Order, Tonight Show, Property Brothers, House Hunters, Love it or List it, Game of Thrones, True Detective, Sesame Street}

Example $\PageIndex{15}$

Use the mapping to

determine whether the relation is a function
find the domain of the relation
find the range of the relation.

Neal	123-567-4839 work 231-378-5941 cell
Krystal	743-469-9731 cell
Kelvin	567-534-2970 work
George	684-369-7231 cell
Christa	684-369-7231 cell
Mike	639-847-6971 cell

Answer: ⓐ No ⓑ {Neal, Krystal, Kelvin, George, Christa, Mike} ⓒ {123-567-4839 work, 231-378-5941 cell, 743-469-9731 cell, 567-534-2970 work, 684-369-7231 cell, 798-367-8541 cell, 639-847-6971 cell}

In algebra, more often than not, functions will be represented by an equation. It is easiest to see if the equation is a function when it is solved for y. If each value of x results in only one value of y, then the equation defines a function.

Example $\PageIndex{16}$

Determine whether each equation is a function.

$2x+y=7$
$y=x^2+1$
$x+y^2=3$

Answer

ⓐ $2x+y=7$

For each value of x, we multiply it by $−2$ and then add 7 to get the y-value

	$.$
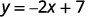
For example, if $x=3$:	$.$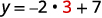
	$.$

We have that when $x=3$, then $y=1$. It would work similarly for any value of x. Since each value of x, corresponds to only one value of y the equation defines a function.

ⓑ $y=x^2+1$

For each value of x, we square it and then add 1 to get the y-value.

	$.$
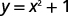
For example, if $x=2$:	$.$
	$.$

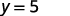
We have that when $x=2$, then $y=5$. It would work similarly for any value of x. Since each value of x, corresponds to only one value of y the equation defines a function.

ⓒ

	$.$
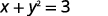
Isolate the y term.	$.$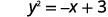
Let’s substitute $x=2$.	$.$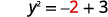
	$.$
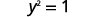
This give us two values for y.	$y=1\space y=−1$

We have shown that when $x=2$, then $y=1$ and $y=−1$. It would work similarly for any value of x. Since each value of x does not corresponds to only one value of y the equation does not define a function.

Example $\PageIndex{17}$

Determine whether each equation is a function.

$4x+y=−3$
$x+y^2=1$
$y−x^2=2$

Answer: ⓐ yes ⓑ no ⓒ yes

Example $\PageIndex{18}$

Determine whether each equation is a function.

$x+y^2=4$
$y=x^2−7$
$y=5x−4$

Answer: ⓐ no ⓑ yes ⓒ yes

Find the Value of a Function

It is very convenient to name a function and most often we name it f, g, h, F, G, or H. In any function, for each x-value from the domain we get a corresponding y-value in the range. For the function $f$, we write this range value $y$ as $f(x)$. This is called function notation and is read $f$ of $x$ or the value of $f$ at $x$. In this case the parentheses does not indicate multiplication.

Definition: Function Notation

For the function $y=f(x)$

\[\begin{array} {l} {f\text{ is the name of the function}} \\{x \text{ is the domain value}} \\ {f(x) \text{ is the range value } y \text{ corresponding to the value } x} \\ \nonumber \end{array}\]

We read $f(x)$ as $f$ of $x$ or the value of $f$ at $x$.

We call x the independent variable as it can be any value in the domain. We call y the dependent variable as its value depends on x.

INDEPENDENT AND DEPENDENT VARIABLES

For the function $y=f(x)$,

\[\begin{array} {l} {x \text{ is the independent variable as it can be any value in the domain}} \\ {y \text{ the dependent variable as its value depends on } x} \\ \nonumber \end{array}\]

Much as when you first encountered the variable x, function notation may be rather unsettling. It seems strange because it is new. You will feel more comfortable with the notation as you use it.

Let’s look at the equation $y=4x−5$. To find the value of y when $x=2$, we know to substitute $x=2$ into the equation and then simplify.

	$.$
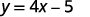Let x=2.	$.$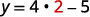
	$.$

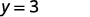The value of the function at $x=2$ is 3.

We do the same thing using function notation, the equation $y=4x−5$ can be written as $f(x)=4x−5$. To find the value when $x=2$, we write:

	$.$
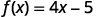Let x=2.	$.$
	$.$

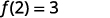The value of the function at $x=2$ is 3.

This process of finding the value of $f(x)$ for a given value of x is called evaluating the function.

Example $\PageIndex{19}$

For the function $f(x)=2x^2+3x−1$, evaluate the function.

$f(3)$
$f(−2)$
$f(a)$

Answer

ⓐ

	$.$
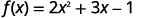
To evaluate $f(3)$, substitute 3 for x.	$.$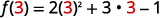
Simplify.	$.$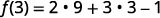
	$.$
	$.$

ⓑ

		$.$
$.$		$.$
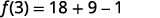
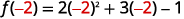
Simplify.		$.$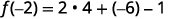
		$.$
		$.$

ⓒ

	$.$
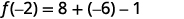
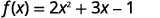
To evaluate f(a),f(a), substitute a for x.	$.$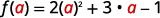
Simplify.	$.$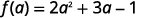

Example $\PageIndex{20}$

For the function $f(x)=3x^2−2x+1$, evaluate the function.

$f(3)$
$f(−1)$
$f(t)$

Example $\PageIndex{21}$

For the function $f(x)=2x^2+4x−3$, evaluate the function.

$f(2)$
$f(−3)$
$f(h)$

In the last example, we found $f(x)$ for a constant value of x. In the next example, we are asked to find $g(x)$ with values of x that are variables. We still follow the same procedure and substitute the variables in for the x.

Example $\PageIndex{22}$

For the function $g(x)=3x−5$, evaluate the function.

$g(h^2)$
$g(x+2)$
$g(x)+g(2)$

Answer

ⓐ

			$.$
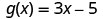
To evaluate $g(h^2)$, substitute $h^2$ for x.			$.$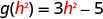
			$.$

ⓑ

	$.$
To evaluate $g(x+2)$, substitute $x+2$ for x.	$.$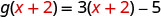
Simplify.	$.$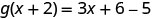
	$.$

ⓒ

		$.$
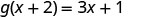
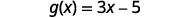
To evaluate $g(x)+g(2)$, first find $g(2)$.		$.$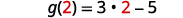
		$.$
$.$		$.$
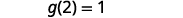
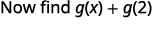
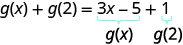
Simplify.		$.$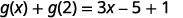
		$.$

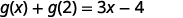
Notice the difference between part ⓑ and ⓒ. We get $g(x+2)=3x+1$ and $g(x)+g(2)=3x−4$. So we see that $g(x+2)\neq g(x)+g(2)$.

Example $\PageIndex{23}$

For the function $g(x)=4x−7$, evaluate the function.

$g(m^2)$
$g(x−3)$
$g(x)−g(3)$

Example $\PageIndex{24}$

For the function $h(x)=2x+1$, evaluate the function.

$h(k^2)$
$h(x+1)$
$h(x)+h(1)$

Many everyday situations can be modeled using functions.

Example $\PageIndex{25}$

The number of unread emails in Sylvia’s account is 75. This number grows by 10 unread emails a day. The function $N(t)=75+10t$ represents the relation between the number of emails, N, and the time, t, measured in days.

Determine the independent and dependent variable.
Find $N(5)$. Explain what this result means.

Answer

ⓐ The number of unread emails is a function of the number of days. The number of unread emails, N, depends on the number of days, t. Therefore, the variable N, is the dependent variable and the variable tt is the independent variable.

ⓑ Find $N(5)$. Explain what this result means.

	$.$
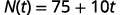
Substitute in t=5.t=5.	$.$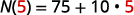
Simplify.	$.$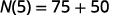
	$.$

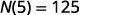
Since 5 is the number of days, $N(5)$, is the number of unread emails after 5 days. After 5 days, there are 125 unread emails in the account.

Example $\PageIndex{26}$

The number of unread emails in Bryan’s account is 100. This number grows by 15 unread emails a day. The function $N(t)=100+15t$ represents the relation between the number of emails, N, and the time, t, measured in days.

Determine the independent and dependent variable.
Find $N(7)]$. Explain what this result means.

Answer: ⓐ t IND; N DEP ⓑ 205; the number of unread emails in Bryan’s account on the seventh day.

Example $\PageIndex{27}$

The number of unread emails in Anthony’s account is 110. This number grows by 25 unread emails a day. The function $N(t)=110+25t$ represents the relation between the number of emails, N, and the time, t, measured in days.

Determine the independent and dependent variable.
Find $N(14)$. Explain what this result means.

Answer: ⓐ t IND; N DEP ⓑ 460; the number of unread emails in Anthony’s account on the fourteenth day

Access this online resource for additional instruction and practice with relations and functions.

Introduction to Functions

Key Concepts

Function Notation: For the function $y=f(x)$
- f is the name of the function
- x is the domain value
- $f(x)$ is the range value y corresponding to the value x
  We read $f(x)$ as f of x or the value of f at x.
Independent and Dependent Variables: For the function $y=f(x)$,
- x is the independent variable as it can be any value in the domain
- y is the dependent variable as its value depends on x

Glossary

domain of a relation: The domain of a relation is all the x-values in the ordered pairs of the relation.

function: A function is a relation that assigns to each element in its domain exactly one element in the range.

mapping: A mapping is sometimes used to show a relation. The arrows show the pairing of the elements of the domain with the elements of the range.

range of a relation: The range of a relation is all the y-values in the ordered pairs of the relation.

relation: A relation is any set of ordered pairs,(x,y).(x,y). All the x-values in the ordered pairs together make up the domain. All the y-values in the ordered pairs together make up the range.

Search

Text Color

Text Size

Margin Size

Font Type

Definition: Relation

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

MAPPING

Example \(\PageIndex{4}\)

Example \(\PageIndex{5}\)

Example \(\PageIndex{6}\)

Example \(\PageIndex{7}\)

Example \(\PageIndex{8}\)

Example \(\PageIndex{9}\)

Definition: Function

Example \(\PageIndex{10}\)

Example \(\PageIndex{11}\)

Example \(\PageIndex{12}\)

Example \(\PageIndex{13}\)

Example \(\PageIndex{14}\)

Example \(\PageIndex{15}\)

Example \(\PageIndex{16}\)

Example \(\PageIndex{17}\)

Example \(\PageIndex{18}\)

Definition: Function Notation

INDEPENDENT AND DEPENDENT VARIABLES

Example \(\PageIndex{19}\)

Example \(\PageIndex{20}\)

Example \(\PageIndex{21}\)

Example \(\PageIndex{22}\)

Example \(\PageIndex{23}\)

Example \(\PageIndex{24}\)

Example \(\PageIndex{25}\)

Example \(\PageIndex{26}\)

Example \(\PageIndex{27}\)

	$.$
Isolate the y term.	$.$
Let’s substitute \(x=2\).	$.$
	$.$
This give us two values for y.	\(y=1\space y=−1\)

	$.$
To evaluate \(f(3)\), substitute 3 for x.	$.$
Simplify.	$.$
	$.$
	$.$

	$.$
To evaluate \(g(x+2)\), substitute \(x+2\) for x.	$.$
Simplify.	$.$
	$.$

		$.$
To evaluate \(g(x)+g(2)\), first find \(g(2)\).		$.$
		$.$
$.$		$.$
Simplify.		$.$
		$.$