3.5E: Exercises

Last updated
Save as PDF

Page ID: 30304

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Verify Solutions to an Inequality in Two Variables

In the following exercises, determine whether each ordered pair is a solution to the given inequality.

1. Determine whether each ordered pair is a solution to the inequality $y>x−1$:

a. $(0,1)$
b. $(−4,−1)$
c. $(4,2)$
d. $(3,0)$
e. $(−2,−3)$

Answer: a. yes b. yes c. no d. no e. no

2. Determine whether each ordered pair is a solution to the inequality $y>x−3$:

a. $(0,0)$
b. $(2,1)$
c. $(−1,−5)$
d. $(−6,−3)$
e. $(1,0)$

3. Determine whether each ordered pair is a solution to the inequality $y<3x+2$:

a. $(0,3)$
b. $(−3,−2)$
c. $(−2,0)$
d. $(0,0)$
e. $(−1,4)$

Answer: a. no b. no c. yes d. yes e. no

4. Determine whether each ordered pair is a solution to the inequality $y<−2x+5$:

a. $(−3,0)(−3,0)
b. \((1,6)$
c. $(−6,−2)$
d. $(0,1)$
e. $(5,−4)$

5. Determine whether each ordered pair is a solution to the inequality $3x−4y>4$:

a. $(5,1)$
b. $(−2,6)$
c. $(3,2)$
d. $(10,−5)$
e. $(0,0)$

Answer: a. yes b. no c. no d. no e. no

6. Determine whether each ordered pair is a solution to the inequality $2x+3y>2$:

a. $(1,1)$
b. $(4,−3)$
c. $(0,0)$
d. $(−8,12)$
e. $(3,0)$

Recognize the Relation Between the Solutions of an Inequality and its Graph

In the following exercises, write the inequality shown by the shaded region.

7. Write the inequality shown by the graph with the boundary line $y=3x−4$.

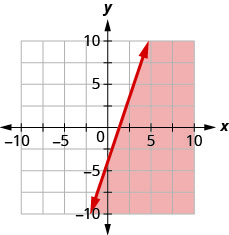
$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, negative 4), (1, negative 1), and (2, 2). The line divides the x y-coordinate plane into two halves. The line and the bottom right half are shaded red to indicate that this is where the solutions of the inequality are.$

Answer: $y\leq 3x−4$

8. Write the inequality shown by the graph with the boundary line $y=2x−4$.

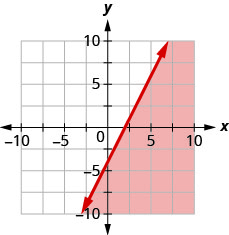
$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, negative 4), (1, negative 2), and (2, 0). The line divides the x y-coordinate plane into two halves. The line and the bottom right half are shaded red to indicate that this is where the solutions of the inequality are.$

9. Write the inequality shown by the graph with the boundary line $y=−\frac{1}{2}x+1$.

$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, 1), (2, 0), and (4, negative 1). The line divides the x y-coordinate plane into two halves. The line and the bottom right half are shaded red to indicate that this is where the solutions of the inequality are.$

Answer: $y\leq −\frac{1}{2}x+1$

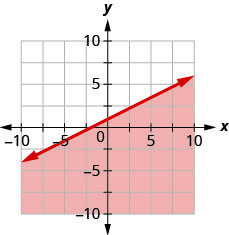
10. Write the inequality shown by the graph with the boundary line $y=-\frac{1}{3}x−2$.

$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, negative 2), (3, negative 3), and (6, negative 4). The line divides the x y-coordinate plane into two halves. The line and the bottom left half are shaded red to indicate that this is where the solutions of the inequality are.$

11. Write the inequality shown by the shaded region in the graph with the boundary line $x+y=5$.

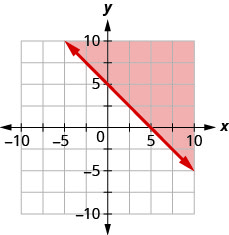
$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, 5), (1, 4), and (5, 0). The line divides the x y-coordinate plane into two halves. The line and the top right half are shaded red to indicate that this is where the solutions of the inequality are.$

Answer: $x+y\geq 5$

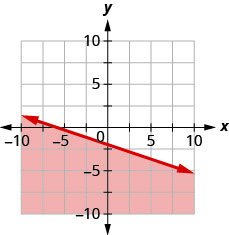
12. Write the inequality shown by the shaded region in the graph with the boundary line $x+y=3$.

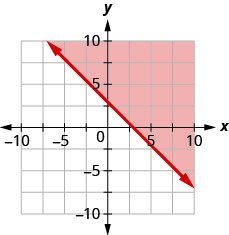
$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, 3), (1, 2), and (3, 0). The line divides the x y-coordinate plane into two halves. The line and the top right half are shaded red to indicate that this is where the solutions of the inequality are.$

13. Write the inequality shown by the shaded region in the graph with the boundary line $3x−y=6$.

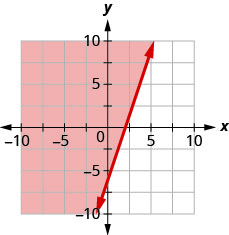
$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, negative 6), (1, negative 3), and (2, 0). The line divides the x y-coordinate plane into two halves. The line and the top left half are shaded red to indicate that this is where the solutions of the inequality are.$

Answer: $3x−y\leq 6$

14. Write the inequality shown by the shaded region in the graph with the boundary line $2x−y=4$.

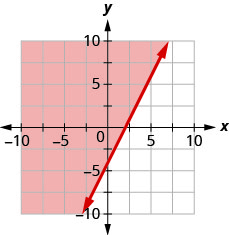
$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, negative 4), (1, negative 2), and (2, 0). The line divides the x y-coordinate plane into two halves. The line and the top left half are shaded red to indicate that this is where the solutions of the inequality are.$

Graph Linear Inequalities in Two Variables

In the following exercises, graph each linear inequality.

15. Graph the linear inequality: $y>\frac{2}{3}x−1$.

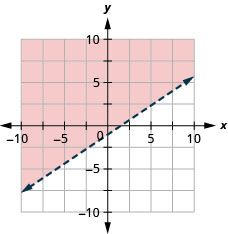
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, negative 1), (3, 1), and (6, 3). The line divides the x y-coordinate plane into two halves. The top left half is shaded red to indicate that this is where the solutions of the inequality are.$

16. Graph the linear inequality: $y<\frac{3}{5}x+2$.

17. Graph the linear inequality: $y\leq −\frac{1}{2}x+4$.

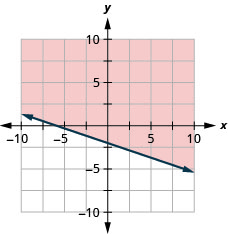
Answer: $This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, 4), (2, 3), and (4, 2). The line divides the x y-coordinate plane into two halves. The line and the top right half are shaded red to indicate that this is where the solutions of the inequality are.$

18. Graph the linear inequality: $y\geq −\frac{1}{3}x−2$.

19. Graph the linear inequality: $x−y\leq 3$.

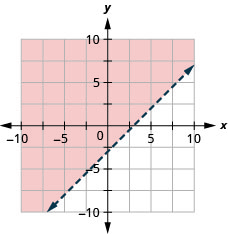
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, negative 3), (1, negative 2), and (3, 0). The line divides the x y-coordinate plane into two halves. The top left half is shaded red to indicate that this is where the solutions of the inequality are.$

20. Graph the linear inequality: $x−y\geq −2$.

21. Graph the linear inequality: $4x+y>−4$.

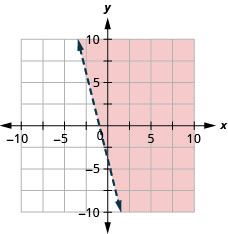
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, negative 4), (negative 1, 0), and (1, negative 8). The line divides the x y-coordinate plane into two halves. The top right half is shaded red to indicate that this is where the solutions of the inequality are.$

22. Graph the linear inequality: $x+5y<−5$.

23. Graph the linear inequality: $3x+2y\geq −6$.

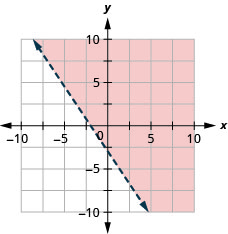
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, negative 3), (3, negative 5), and (negative 2, 0). The line divides the x y-coordinate plane into two halves. The top right half is shaded red to indicate that this is where the solutions of the inequality are.$

24. Graph the linear inequality: $4x+2y\geq −8$.

25. Graph the linear inequality: $y>4x$.

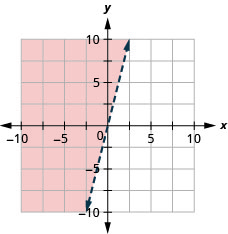
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, 0), (negative 1, negative 4), and (1, 4). The line divides the x y-coordinate plane into two halves. The top left half is shaded red to indicate that this is where the solutions of the inequality are.$

26. Graph the linear inequality: $y\leq −3x$.

27. Graph the linear inequality: $y<−10$.

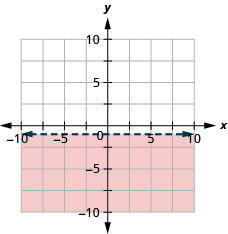
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, 0), (negative 1, 3), and (1, negative 3). The line divides the x y-coordinate plane into two halves. The bottom left half is shaded red to indicate that this is where the solutions of the inequality are.$

28. Graph the linear inequality: $y\geq 2$.

29. Graph the linear inequality: $x\leq 5$.

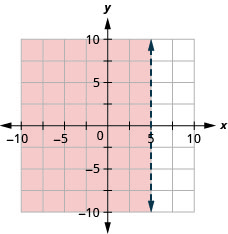
Answer: $This figure has the graph of a straight vertical dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A vertical dashed line is drawn through the points (5, negative 1), (5, 0), and (5, 1). The line divides the x y-coordinate plane into two halves. The left half is shaded red to indicate that this is where the solutions of the inequality are.$

30. Graph the linear inequality: $x\geq 0$.

31. Graph the linear inequality: $x−y<4$.

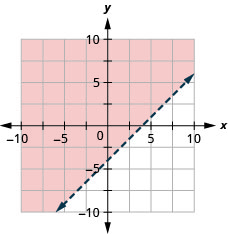
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, negative 4), (1, negative 3), and (4, 0). The line divides the x y-coordinate plane into two halves. The top left half is shaded red to indicate that this is where the solutions of the inequality are.$

32. Graph the linear inequality: $x−y<−3$.

33. Graph the linear inequality: $y\geq \frac{3}{2}x$.

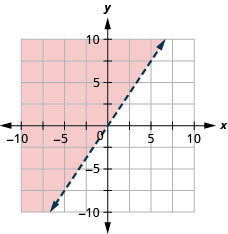
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, 0), (2, 3), and (negative 2, negative 3). The line divides the x y-coordinate plane into two halves. The top left half is shaded red to indicate that this is where the solutions of the inequality are.$

34. Graph the linear inequality: $y\leq \frac{5}{4}x$.

35. Graph the linear inequality: $y>−2x+1$.

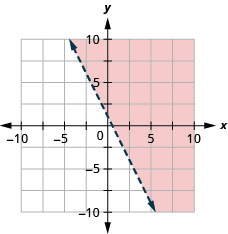
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, 1), (1, negative 1), and (2, negative 3). The line divides the x y-coordinate plane into two halves. The top right half is shaded red to indicate that this is where the solutions of the inequality are.$

36. Graph the linear inequality: $y<−3x−4$.

37. Graph the linear inequality: $2x+y\geq −4$.

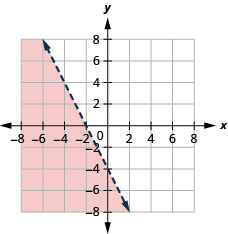
Answer: $This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, negative 4), (1, negative 6), and (negative 2, 0). The line divides the x y-coordinate plane into two halves. The line and the bottom left half are shaded red to indicate that this is where the solutions of the inequality are.$

38. Graph the linear inequality: $x+2y\leq −2$.

39. Graph the linear inequality: $2x−5y>10$.

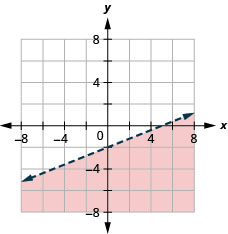
Answer: $This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, negative 2), (5, 0), and (negative 5, negative 4). The line divides the x y-coordinate plane into two halves. The line and the bottom right half are shaded red to indicate that this is where the solutions of the inequality are.$

40. Graph the linear inequality: $4x−3y>12$.

Solve Applications using Linear Inequalities in Two Variables

41. Harrison works two part time jobs. One at a gas station that pays $11 an hour and the other is IT troubleshooting for $16.50$16.50an hour. Between the two jobs, Harrison wants to earn at least $330 a week. How many hours does Harrison need to work at each job to earn at least $330?

a. Let x be the number of hours he works at the gas station and let y be the number of (hours he works troubleshooting. Write an inequality that would model this situation.

b. Graph the inequality.

c. Find three ordered pairs $(x,y)$ that would be solutions to the inequality. Then, explain what that means for Harrison.

Answer

a. $11x+16.5y\geq 330$
b.

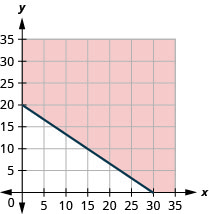
$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from 0 to 35. A line is drawn through the points (0, 20), (15, 10), and (30, 0). The line divides the x y-coordinate plane into two halves. The line and the top right half are shaded red to indicate that this is where the solutions of the inequality are.$

c. Answers will vary.

42. Elena needs to earn at least $450 a week during her summer break to pay for college. She works two jobs. One as a swimming instructor that pays $9 an hour and the other as an intern in a genetics lab for $22.50 per hour. How many hours does Elena need to work at each job to earn at least $450 per week?

a. Let x be the number of hours she works teaching swimming and let y be the number of hours she works as an intern. Write an inequality that would model this situation.

b. Graph the inequality.

c. Find three ordered pairs (x,y)(x,y) that would be solutions to the inequality. Then, explain what that means for Elena.

43. The doctor tells Laura she needs to exercise enough to burn 500 calories each day. She prefers to either run or bike and burns 15 calories per minute while running and 10 calories a minute while biking.

a. If x is the number of minutes that Laura runs and y is the number minutes she bikes, find the inequality that models the situation.

b. Graph the inequality.

c. List three solutions to the inequality. What options do the solutions provide Laura?

Answer

a. $15x+10y\geq 500$
b.

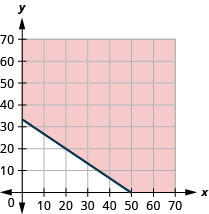
$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from 0 to 60. A line is drawn through the points (0, 50) and (20, 20). The line divides the x y-coordinate plane into two halves. The line and the top right half are shaded red to indicate that this is where the solutions of the inequality are.$

c. Answers will vary.

44. Armando’s workouts consist of kickboxing and swimming. While kickboxing, he burns 10 calories per minute and he burns 7 calories a minute while swimming. He wants to burn 600 calories each day.

a. If x is the number of minutes that Armando will kickbox and y is the number minutes he will swim, find the inequality that will help Armando create a workout for today.

b. Graph the inequality.

c. List three solutions to the inequality. What options do the solutions provide Armando?

Writing Exercises

45. Lester thinks that the solution of any inequality with a >> sign is the region above the line and the solution of any inequality with a << sign is the region below the line. Is Lester correct? Explain why or why not.

Answer: Answers will vary.

46. Explain why, in some graphs of linear inequalities, the boundary line is solid but in other graphs it is dashed.

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$This table has 4 rows and 4 columns. The first row is a header row and it labels each column. The first column header is “I can…”, the second is “Confidently”, the third is “With some help”, and the fourth is “No, I don’t get it”. Under the first column are the phrases “verify solutions to an inequality in two variables.”, “recognize the relation between the solutions of an inequality and its graph”, and “graph linear inequalities”. The other columns are left blank so that the learner may indicate their mastery level for each topic.$

b. On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Search

Text Color

Text Size

Margin Size

Font Type