Chapter 3 Review Exercises

Last updated
Save as PDF

Page ID: 18494

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Chapter Review Exercises

Graph Linear Equations in Two Variables

Plot Points in a Rectangular Coordinate System

In the following exercises, plot each point in a rectangular coordinate system.

1. ⓐ $(−1,−5)$
ⓑ $(−3,4)$
ⓒ $(2,−3)$
ⓓ $(1,\frac{5}{2})$

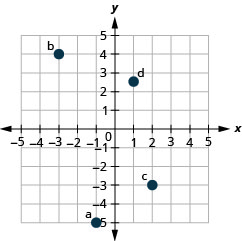
Answer: $This figure shows points plotted on the x y-coordinate plane. The x and y axes run from negative 5 to 5. The point labeled a is 1 units to the left of the origin and 5 units below the origin and is located in quadrant III. The point labeled b is 3 units to the left of the origin and 4 units above the origin and is located in quadrant II. The point labeled c is 2 units to the right of the origin and 3 units below the origin and is located in quadrant IV. The point labeled d is 1 unit to the right of the origin and 2.5 units above the origin and is located in quadrant I.$

2. ⓐ $(−2,0)$
ⓑ $(0,−4)$
ⓒ $(0,5)$
ⓓ $(3,0)$

In the following exercises, determine which ordered pairs are solutions to the given equations.

3. $5x+y=10$;

ⓐ $(5,1)$
ⓑ $(2,0)$
ⓒ $(4,−10)$

Answer: ⓑ, ⓒ

4. $y=6x−2$;

ⓐ $(1,4)$
ⓑ $(13,0)$
ⓒ $(6,−2)$

Graph a Linear Equation by Plotting Points

In the following exercises, graph by plotting points.

5. $y=4x−3$

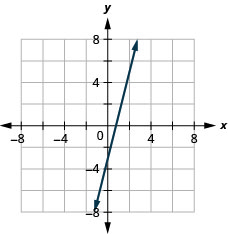
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 1, negative 7), (0, negative 3), (1, negative 1), and (2, 3).$

6. $y=−3x$

7. $y=\frac{1}{2}x+3$

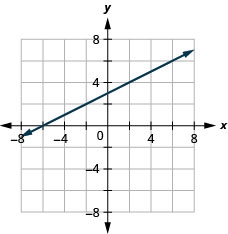
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 6, 0), (0, 3), (2, 4), and (4, 5).$

8. $y=−\frac{4}{5}|x−1$

9. $x−y=6$

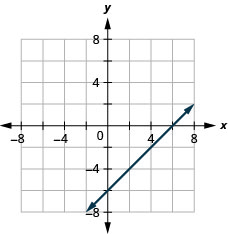
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 1, negative 7), (0, negative 6), (3, negative 3), and (6, 0).$

10. $2x+y=7$

11. $3x−2y=6$

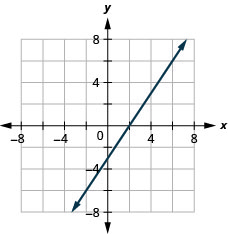
Answer: $This figure shows a straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (negative 2, negative 6), (0, negative 3), (2, 0), and (4, 3).$

Graph Vertical and Horizontal lines

In the following exercises, graph each equation.

12. $y=−2$

13. $x=3$

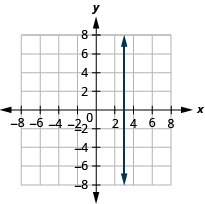
Answer: $This figure shows a vertical straight line graphed on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (3, negative 1), (3, 0), and (3, 1).$

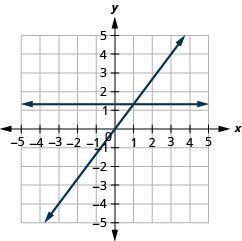
In the following exercises, graph each pair of equations in the same rectangular coordinate system.

14. $y=−2x$ and $y=−2$

15. $y=\frac{4}{3}x$ and $y=\frac{4}{3}$

Answer: $The figure shows the graphs of a straight horizontal line and a straight slanted line on the same x y-coordinate plane. The x and y axes run from negative 5 to 5. The horizontal line goes through the points (0, 4 divided by 3), (1, 4 divided by 3), and (2, 4 divided by 3). The slanted line goes through the points (0, 0), (1, 4 divided by 3), and (2, 8 divided by 3).$

Find x- and y-Intercepts

In the following exercises, find the x- and y-intercepts.

16.
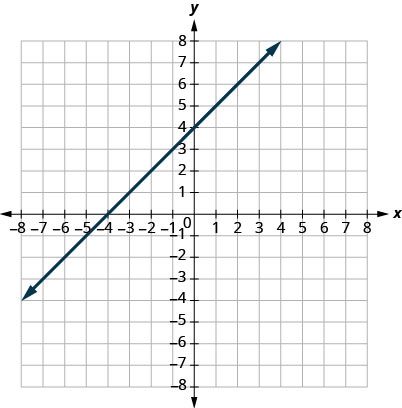
$The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 6, negative 2), (negative 4, 0), (negative 2, 2), (0, 4), (2, 6), and (4, 8).$

17.
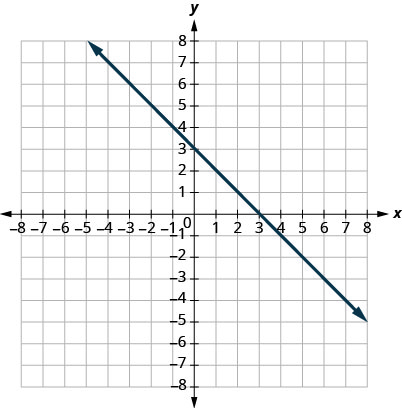
$The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 2, 5), (negative 1, 4), (0, 3), (3, 0), and (6, negative 3).$

Answer: $(0,3)(3,0)$

In the following exercises, find the intercepts of each equation.

18. $x−y=−1$

19. $x+2y=6$

Answer: $(6,0),\space (0,3)$

20. $2x+3y=12$

21. $y=\frac{3}{4}x−12$

Answer: $(16,0),\space (0,−12)$

22. $y=3x$

Graph a Line Using the Intercepts

In the following exercises, graph using the intercepts.

23. $−x+3y=3$

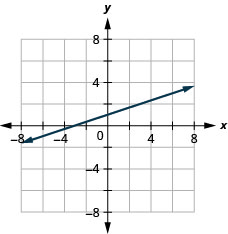
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 3, 0), (0, 1), (3, 2), and (6, 3).$

24. $x−y=4$

25. $2x−y=5$

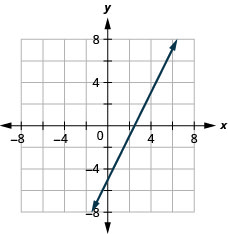
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (0, negative 5), (1, negative 3), (2, negative 1), and (3, 1).$

26. $2x−4y=8$

27. $y=4x$

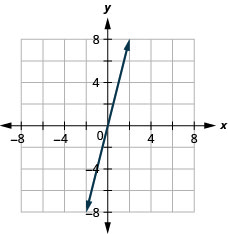
Answer: $The figure shows a straight line graphed on the x y-coordinate plane. The x and y axes run from negative 8 to 8. The line goes through the points (negative 1, 4), (0, 0), and (1, negative 4).$

Slope of a Line

Find the Slope of a Line

In the following exercises, find the slope of each line shown.

28.
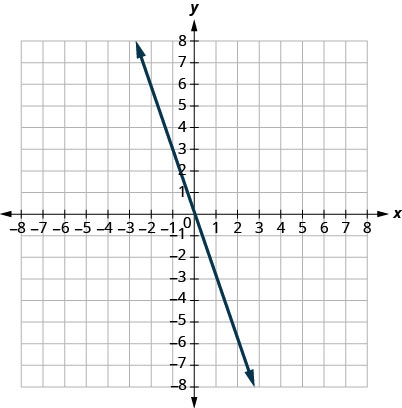
$This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (0, 0) and (1, negative 3).$

29.
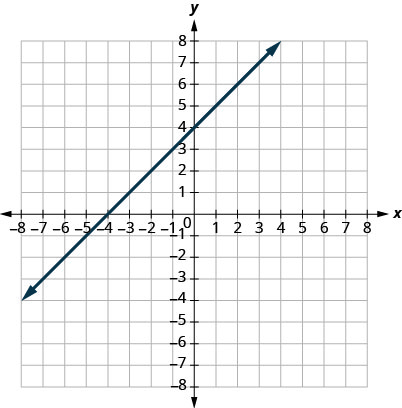
$This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (negative 4, 0) and (0, 4).$

Answer: 1

30.
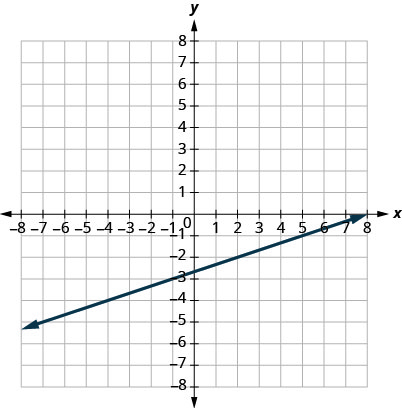
$This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (negative 4, negative 4) and (2, negative 2).$

31.
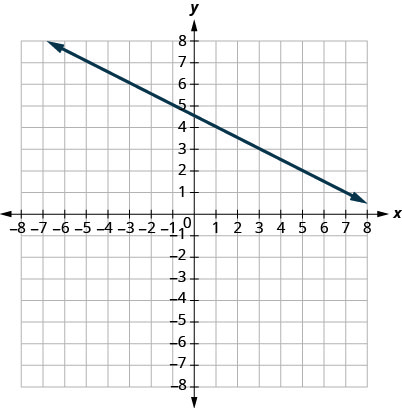
$This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (1, 4) and (5, 2).$

Answer: $−12$

In the following exercises, find the slope of each line.

32. $y=2$

33. $x=5$

Answer: undefined

34. $x=−3$

35. $y=−1$

Answer: 0

Use the Slope Formula to find the Slope of a Line between Two Points

In the following exercises, use the slope formula to find the slope of the line between each pair of points.

36. $(−1,−1),(0,5)$

37. $(3.5),(4,−1)$

Answer: $−6$

38. $(−5,−2),(3,2)$

39. $(2,1),(4,6)$

Answer: $52$

Graph a Line Given a Point and the Slope

In the following exercises, graph each line with the given point and slope.

40. $(2,−2);\space m=52$

41. $(−3,4);\space m=−13$

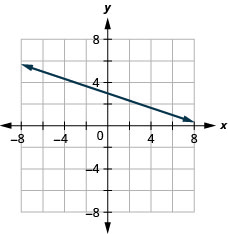
Answer: $This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (negative 3, 4) and (0, 3).$

42. $x$-intercept $−4; m=3$

43. $y$-intercept $1; m=−34$

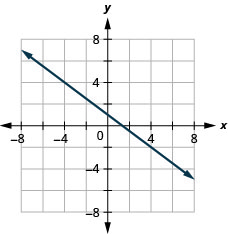
Answer: $This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, 1) and (4, negative 2).$

Graph a Line Using Its Slope and Intercept

In the following exercises, identify the slope and $y$-intercept of each line.

44. $y=−4x+9$

45. $y=53x−6$

Answer: $m=53;\space (0,−6)$

46. $5x+y=10$

47. $4x−5y=8$

Answer: $m=\frac{4}{5};\space (0,−\frac{8}{5})$

In the following exercises, graph the line of each equation using its slope and y-intercept.

48. $y=2x+3$

49. $y=−x−1$

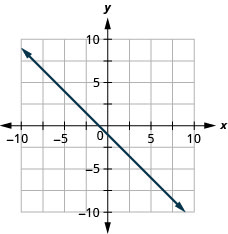
Answer: $This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (0, negative 1) and (1, negative 2).$

50. $y=−25x+3$

51. $4x−3y=12$

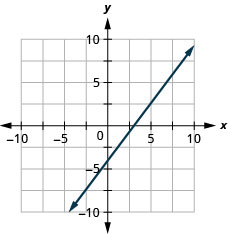
Answer: $This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (0, negative 4) and (3, 0).$

In the following exercises, determine the most convenient method to graph each line.

52. $x=5$

53. $y=−3$

Answer: horizontal line

54. $2x+y=5$

55. $x−y=2$

Answer: intercepts

56. $y=22x+2$

57. $y=34x−1$

Answer: plotting points

Graph and Interpret Applications of Slope-Intercept

58. Katherine is a private chef. The equation $C=6.5m+42$ models the relation between her weekly cost, C, in dollars and the number of meals, m, that she serves.

ⓐ Find Katherine’s cost for a week when she serves no meals.
ⓑ Find the cost for a week when she serves 14 meals.
ⓒ Interpret the slope and C-intercept of the equation.
ⓓ Graph the equation.

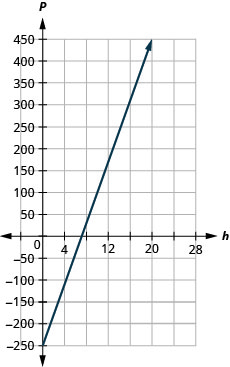
59. Marjorie teaches piano. The equation $P=35h−250$ models the relation between her weekly profit, P, in dollars and the number of student lessons, s, that she teaches.

ⓐ Find Marjorie’s profit for a week when she teaches no student lessons.
ⓑ Find the profit for a week when she teaches 20 student lessons.
ⓒ Interpret the slope and P-intercept of the equation.
ⓓ Graph the equation.

Answer

ⓐ $−$250$
ⓑ $$450$
ⓒ The slope, 35, means that Marjorie’s weekly profit, P, increases by $35 for each additional student lesson she teaches.
The P-intercept means that when the number of lessons is 0, Marjorie loses $250.
ⓓ

$This figure shows the graph of a straight line on the x y-coordinate plane. The x-axis runs from negative 4 to 28. The y-axis runs from negative 250 to 450. The line goes through the points (0, negative 250) and (20, 450).$

Use Slopes to Identify Parallel and Perpendicular Lines

In the following exercises, use slopes and $y$-intercepts to determine if the lines are parallel, perpendicular, or neither.

60. $4x−3y=−1;\quad y=43x−3$

61. $y=5x−1;\quad 10x+2y=0$

Answer: neither

62. $3x−2y=5;\quad 2x+3y=6$

63. $2x−y=8;\quad x−2y=4$

Answer: not parallel

Find the Equation of a Line

Find an Equation of the Line Given the Slope and y-Intercept

In the following exercises, find the equation of a line with given slope and y-intercept. Write the equation in slope–intercept form.

64. Slope $\frac{1}{3}$ and $y$-intercept $(0,−6)$

65. Slope $−5$ and $y$-intercept $(0,−3)$

Answer: $y=−5x−3$

66. Slope $0$ and $y$-intercept $(0,4)$

67. Slope $−2$ and $y$-intercept $(0,0)$

Answer: $y=−2x$

In the following exercises, find the equation of the line shown in each graph. Write the equation in slope–intercept form.

68.
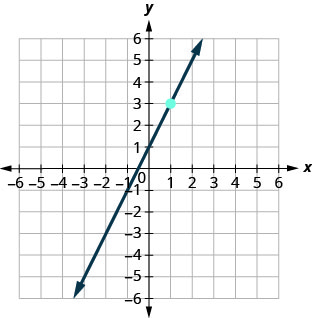
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, 1), (1, 3), and (2, 5).$

69.
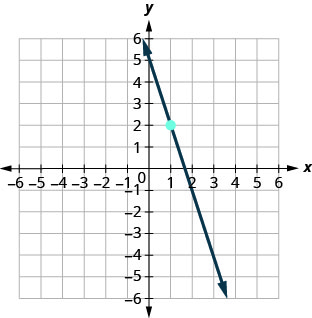
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, 5), (1, 2), and (2, negative 1).$

Answer: $y=−3x+5$

70.
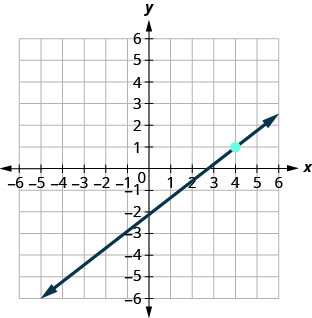
$This figure has a graph of a straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, negative 2), (4, 1), and (8, 4).$

71.
$This figure has a graph of a horizontal straight line on the x y-coordinate plane. The x and y-axes run from negative 10 to 10. The line goes through the points (0, negative 4), (1, negative 4), and (2, negative 4).$

Answer: $y=−4$

Find an Equation of the Line Given the Slope and a Point

In the following exercises, find the equation of a line with given slope and containing the given point. Write the equation in slope–intercept form.

72. $m=−\frac{1}{4}$, point $(−8,3)$

73. $m=\frac{3}{5}$, point $(10,6)$

Answer: $y=\frac{3}{5}x$

74. Horizontal line containing $(−2,7)$

75. $m=−2$, point $(−1,−3)$

Answer: $y=−2x−5$

Find an Equation of the Line Given Two Points

In the following exercises, find the equation of a line containing the given points. Write the equation in slope–intercept form.

76. $(2,10)$ and $(−2,−2)$

77. $(7,1)$ and $(5,0)$

Answer: $y=\frac{1}{2}x−\frac{5}{2}$

78. $(3,8)$ and $(3,−4)$

79. $(5,2)$ and $(−1,2)$

Answer: $y=2$

Find an Equation of a Line Parallel to a Given Line

In the following exercises, find an equation of a line parallel to the given line and contains the given point. Write the equation in slope–intercept form.

80. line $y=−3x+6$, point $(1,−5)$

81. line $2x+5y=−10$, point $(10,4)$

Answer: $y=−\frac{2}{5}x+8$

82. line $x=4$, point $(−2,−1)$

83. line $y=−5$, point $(−4,3)$

Answer: $y=3$

Find an Equation of a Line Perpendicular to a Given Line

In the following exercises, find an equation of a line perpendicular to the given line and contains the given point. Write the equation in slope–intercept form.

84. line $y=−\frac{4}{5}x+2$, point $(8,9)$

85. line $2x−3y=9$, point $(−4,0)$

Answer: $y=−\frac{3}{2}x−6$

86. line $y=3$, point $(−1,−3)$

87. line $x=−5$ point $(2,1)$

Answer: $y=1$

Graph Linear Inequalities in Two Variables

Verify Solutions to an Inequality in Two Variables

In the following exercises, determine whether each ordered pair is a solution to the given inequality.

88. Determine whether each ordered pair is a solution to the inequality $y<x−3$:

ⓐ $(0,1)$ ⓑ $(−2,−4)$ ⓒ $(5,2)$ ⓓ $(3,−1)$
ⓔ $(−1,−5)$

89. Determine whether each ordered pair is a solution to the inequality $x+y>4$:

ⓐ $(6,1)$ ⓑ $(−3,6)$ ⓒ $(3,2)$ ⓓ $(−5,10)$ ⓔ $(0,0)$

Answer: ⓐ yes ⓑ no ⓒ yes ⓓ yes; ⓔ nom

Recognize the Relation Between the Solutions of an Inequality and its Graph

In the following exercises, write the inequality shown by the shaded region.

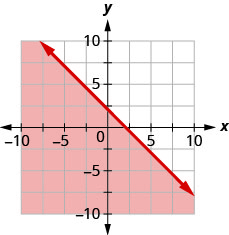
90. Write the inequality shown by the graph with the boundary line $y=−x+2.$

$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, 2), (1, 1), and (2, 0). The line divides the x y-coordinate plane into two halves. The line and the bottom left half are shaded red to indicate that this is where the solutions of the inequality are.$

91. Write the inequality shown by the graph with the boundary line $y=\frac{2}{3}x−3$.

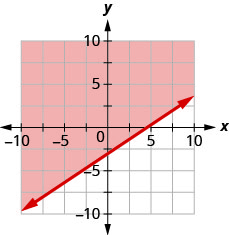
$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, negative 3), (3, negative 1), and (6, 1). The line divides the x y-coordinate plane into two halves. The line and the top left half are shaded red to indicate that this is where the solutions of the inequality are.$

Answer: $y>\frac{2}{3}x−3$

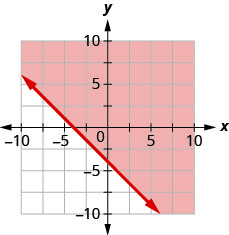
92. Write the inequality shown by the shaded region in the graph with the boundary line $x+y=−4$.

$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, negative 4), (negative 2, negative 2), and (negative 4, 0). The line divides the x y-coordinate plane into two halves. The line and the top right half are shaded red to indicate that this is where the solutions of the inequality are.$

93. Write the inequality shown by the shaded region in the graph with the boundary line $x−2y=6$.

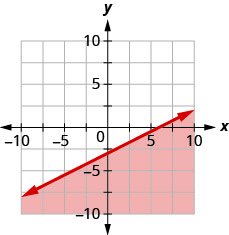
$This figure has the graph of a straight line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A line is drawn through the points (0, negative 3), (2, negative 2), and (6, 0). The line divides the x y-coordinate plane into two halves. The line and the bottom right half are shaded red to indicate that this is where the solutions of the inequality are.$

Answer: $x−2y\geq 6$

Graph Linear Inequalities in Two Variables

In the following exercises, graph each linear inequality.

94. Graph the linear inequality $y>\frac{2}{5}x−4$.

95. Graph the linear inequality $y\leq −\frac{1}{4}x+3$.

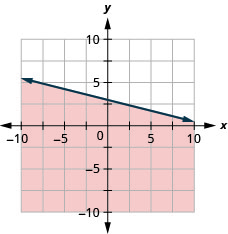
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, 3), (4, 2), and (8, 1). The line divides the x y-coordinate plane into two halves. The bottom left half is shaded red to indicate that this is where the solutions of the inequality are.$

96. Graph the linear inequality $x−y\leq 5$.

97. Graph the linear inequality $3x+2y>10.$

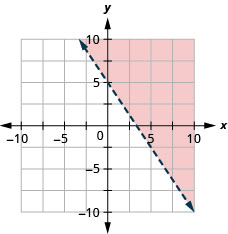
Answer: $This figure has the graph of a straight dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, 5), (2, 2), and (4, negative 1). The line divides the x y-coordinate plane into two halves. The top right half is shaded red to indicate that this is where the solutions of the inequality are.$

98. Graph the linear inequality $y\leq −3x$.

99. Graph the linear inequality $y<6.$

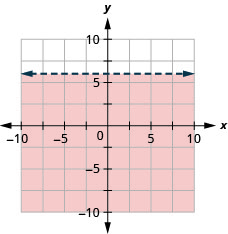
Answer: $This figure has the graph of a straight horizontal dashed line on the x y-coordinate plane. The x and y axes run from negative 10 to 10. A straight dashed line is drawn through the points (0, 6), (1, 6), and (2, 6). The line divides the x y-coordinate plane into two halves. The bottom half is shaded red to indicate that this is where the solutions of the inequality are.$

Solve Applications using Linear Inequalities in Two Variables

100. Shanthie needs to earn at least $500 a week during her summer break to pay for college. She works two jobs. One as a swimming instructor that pays $10 an hour and the other as an intern in a law office for $25 hour. How many hours does Shanthie need to work at each job to earn at least $500 per week?

ⓐ Let x be the number of hours she works teaching swimming and let y be the number of hours she works as an intern. Write an inequality that would model this situation.
ⓑ Graph the inequality.
ⓒ Find three ordered pairs $(x,y)$ that would be solutions to the inequality. Then, explain what that means for Shanthie.

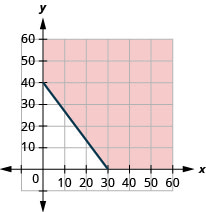
101. Atsushi he needs to exercise enough to burn $600$ calories each day. He prefers to either run or bike and burns $20$ calories per minute while running and $15$ calories a minute while biking.

ⓐ If x is the number of minutes that Atsushi runs and y is the number minutes he bikes, find the inequality that models the situation.
ⓑ Graph the inequality.
ⓒ List three solutions to the inequality. What options do the solutions provide Atsushi?

Answer

ⓐ $20x+15y\geq 60020x+15y\geq 600$
ⓑ

$The figure has a straight line graphed on the x y-coordinate plane. The x-axis runs from 0 to 50. The y-axis runs from 0 to 50. The line goes through the points (0, 40) and (30, 0). The line divides the coordinate plane into two halves. The top right half and the line are colored red to indicate that this is the solution set.$

Relations and Functions

Find the Domain and Range of a Relation

In the following exercises, for each relation, ⓐ find the domain of the relation ⓑ find the range of the relation.

102. ${\{(5,−2),\,(5,−4),\,(7,−6),\,(8,−8),\,(9,−10)}\}$

103. ${\{(−3,7),\,(−2,3),\,(−1,9), \,(0,−3),\,(−1,8)}\}$

Answer: ⓐ $D: {−3, −2, −1, 0}$
ⓑ $R: {7, 3, 9, −3, 8}$

In the following exercise, use the mapping of the relation to ⓐ list the ordered pairs of the relation ⓑ find the domain of the relation ⓒ find the range of the relation.

104. The mapping below shows the average weight of a child according to age.

$This figure shows two table that each have one column. The table on the left has the header “Age (yrs)” and lists the numbers 1, 2, 3, 4, 5, 6, and 7. The table on the right has the header “Weight (pounds)” and lists the numbers 20, 35, 30, 45, 40, 25, and 50. There are arrows starting at numbers in the age table and pointing towards numbers in the weight table. The first arrow goes from 1 to 20. The second arrow goes from 2 to 25. The third arrow goes from 3 to 30. The fourth arrow goes from 4 to 35. The fifth arrow goes from 5 to 40. The sixth arrow goes from 6 to 45. The seventh arrow goes from 7 to 50.$

In the following exercise, use the graph of the relation to ⓐ list the ordered pairs of the relation ⓑ find the domain of the relation ⓒ find the range of the relation.

105.
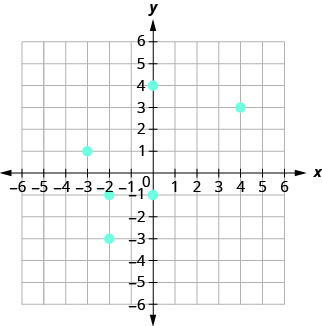
$The figure shows the graph of some points on the x y-coordinate plane. The x and y-axes run from negative 6 to 6. The points (negative 3, 1), (negative 2, negative 1), (negative 2, negative 3), (0, negative 1), (0, 4), and (4, 3).$

Answer: ⓐ $(4, 3), \,(−2, −3), \,(−2, −1), \,(−3, 1), \,(0, −1), \,(0, 4)$
ⓑ $D: {−3, −2, 0, 4}$
ⓒ $R: {−3, −1, 1, 3, 4}$

Determine if a Relation is a Function

In the following exercises, use the set of ordered pairs to ⓐ determine whether the relation is a function ⓑ find the domain of the relation ⓒ find the range of the relation.

106. ${\{(9,−5),\,(4,−3),\,(1,−1),\,(0,0),\,(1,1),\,(4,3),\,(9,5)}\}$

107. ${\{(−3,27),\,(−2,8),\,(−1,1),\,(0,0),\,(1,1),\,(2,8),\,(3,27)}\}$

Answer: ⓐ yes ⓑ ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ ${0, 1, 8, 27}$

In the following exercises, use the mapping to ⓐ determine whether the relation is a function ⓑ find the domain of the function ⓒfind the range of the function.

108.
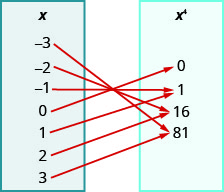
$This figure shows two table that each have one column. The table on the left has the header “x” and lists the numbers negative 3, negative 2, negative 1, 0, 1, 2, and 3. The table on the right has the header “x to the fourth power” and lists the numbers 0, 1, 16, and 81. There are arrows starting at numbers in the x table and pointing towards numbers in the x to the fourth power table. The first arrow goes from negative 3 to 81. The second arrow goes from negative 2 to 16. The third arrow goes from negative 1 to 1. The fourth arrow goes from 0 to 0. The fifth arrow goes from 1 to 1. The sixth arrow goes from 2 to 16. The seventh arrow goes from 3 to 81.$

109.
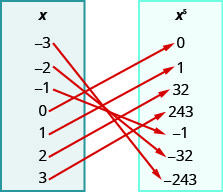
$This figure shows two table that each have one column. The table on the left has the header “x” and lists the numbers negative 3, negative 2, negative 1, 0, 1, 2, and 3. The table on the right has the header “x to the fifth power” and lists the numbers 0, 1, 32, 243, negative 1, negative 32, and negative 243. There are arrows starting at numbers in the x table and pointing towards numbers in the x to the fifth power table. The first arrow goes from negative 3 to negative 243. The second arrow goes from negative 2 to negative 32. The third arrow goes from negative 1 to 1. The fourth arrow goes from 0 to 0. The fifth arrow goes from 1 to 1. The sixth arrow goes from 2 to 32. The seventh arrow goes from 3 to 243.$

Answer: ⓐ ${−3, −2, −1, 0, 1, 2, 3}$
ⓑ ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ ${−243, −32, −1, 0, 1, 32, 243}$

In the following exercises, determine whether each equation is a function.

110. $2x+y=−3$

111. $y=x^2$

Answer: yes

112. $y=3x−5$

113. $y=x^3$

Answer: yes

114. $2x+y2=4$

Find the Value of a Function

In the following exercises, evaluate the function:

ⓐ $f(−2)$ ⓑ $f(3)$ ⓒ $f(a)$.

115. $f(x)=3x−4$

Answer: ⓐ $f(−2)=−10$ ⓑ $f(3)=5$ ⓒ $f(a)=3a−4$

116. $f(x)=−2x+5$

117. $f(x)=x^2−5x+6$

Answer: ⓐ $f(−2)=20$ ⓑ $f(3)=0$ ⓒ $f(a)=a^2−5a+6$

118. $f(x)=3x^2−2x+1$

In the following exercises, evaluate the function.

119. $g(x)=3x2−5x;\space g(2)$

Answer: $2$

120. $F(x)=2x2−3x+1;\space F(−1)$

121. $h(t)=4|t−1|+2;\space h(t)=4$

Answer: $18$

122. $f(x)=x+2x−1;\space f(3)$

Graphs of Functions

Use the Vertical line Test

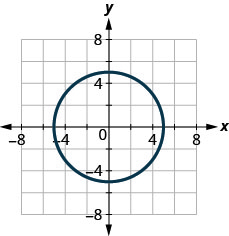
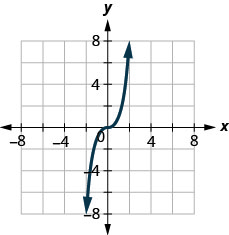
In the following exercises, determine whether each graph is the graph of a function.

123.
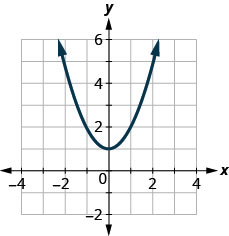
$The figure has a square function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The parabola goes through the points (negative 2, 5), (negative 1, 2), (0, 1), (1, 2), and (2, 5). The lowest point on the graph is (0, 1).$

Answer: yes

124.
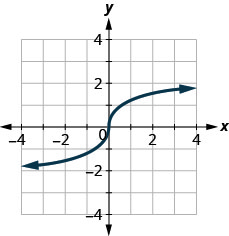
$The figure has an s-shaped function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The curve goes through the points (negative 1, negative 1), (0, 0), and (1, 1).$

125.
$The figure has a circle graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The circle goes through the points (negative 5, 0), (5, 0), (0, negative 5), and (0, 5).$

Answer: no

126.
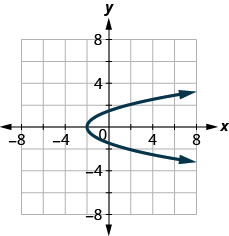
$The figure has a parabola opening to the right graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The parabola goes through the points (negative 2, 0), (negative 1, 1), (negative 1, negative 1), (2, 2), and (2, negative 2). The left-most point on the graph is (negative 2, 0).$

127.
$The figure has a cube function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The curved line goes through the points (negative 1, negative 1), (0, 0), and (1, 1).$

Answer: yes

128.
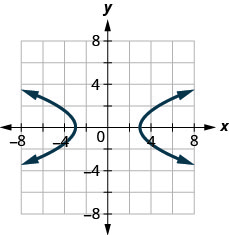
$The figure has two curved lines graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The curved line on the left goes through the points (negative 3, 0), (negative 4, 2), and (negative 4, negative 2). The curved line on the right goes through the points (3, 0), (4, 2), and (4, negative 2).$

129.
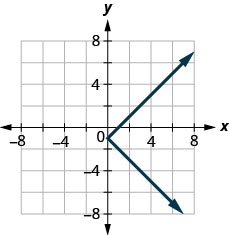
$The figure has a sideways absolute value function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line bends at the point (0, negative 1) and goes to the right. The line goes through the points (1, 0), (1, negative 2), (2, 1), and (2, negative 3).$

Answer: no

Identify Graphs of Basic Functions

In the following exercises, ⓐ graph each function ⓑ state its domain and range. Write the domain and range in interval notation.

130. $f(x)=5x+1$

131. $f(x)=−4x−2$

Answer

ⓐ

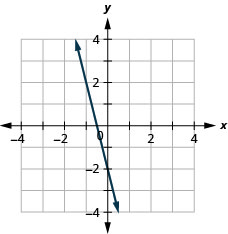
$The figure has a linear function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (negative 2, 6), (negative 1, 2), and (0, negative 2).$

ⓑ $D: (-\inf ,\inf ), R: (-\inf ,\inf )$

132. $f(x)=\frac{2}{3}x−1$

133. $f(x)=−6$

Answer

ⓐ

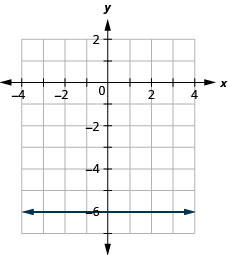
$The figure has a constant function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 8 to 4. The line goes through the points (0, negative 6), (1, negative 6), and (2, negative 6).$

ⓑ $D: (-\inf ,\inf ), R: (-\inf ,\inf )$

134. $f(x)=2x$

135. $f(x)=3x^2$

Answer

ⓐ

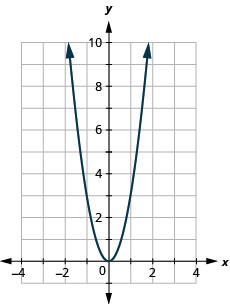
$The figure has a square function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The parabola goes through the points (negative 1, 3), (0, 0), and (1, 3). The lowest point on the graph is (0, 0).$

ⓑ $D: (-\inf ,\inf ), R: (-\inf ,0]$

136. $f(x)=−12x^2$

137. $f(x)=x^2+2$

Answer

ⓐ

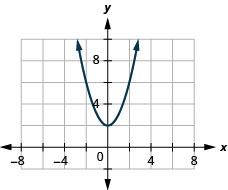
$The figure has a square function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 4 to 8. The parabola goes through the points (negative 2, 6), (negative 1, 3), (0, 2), (1, 3), and (2, 6). The lowest point on the graph is (0, 2).$

ⓑ $D: (-\inf ,\inf ), R: (-\inf ,\inf )$

138. $f(x)=x^3−2$

139. $f(x)=\sqrt{x+2}$

Answer

ⓐ

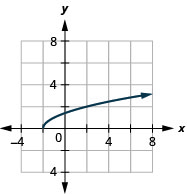
$The figure has a square root function graphed on the x y-coordinate plane. The x-axis runs from negative 4 to 8. The y-axis runs from negative 2 to 10. The half-line starts at the point (negative 2, 0) and goes through the points (negative 1, 1) and (2, 2).$

ⓑ $D: [−2,−2, \inf ), \space R: [0,\inf )$

140. $f(x)=−|x|$

141. $f(x)=|x|+1$

Answer

ⓐ

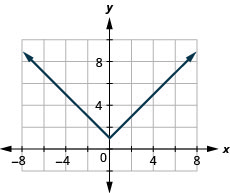
$The figure has an absolute value function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The vertex is at the point (0, 1). The line goes through the points (negative 1, 2) and (1, 2).$

ⓑ $D: (-\inf ,\inf ), \space R: [1,\inf )$

Read Information from a Graph of a Function

In the following exercises, use the graph of the function to find its domain and range. Write the domain and range in interval notation

142.
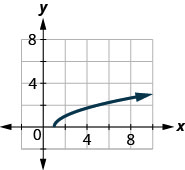
$The figure has a square root function graphed on the x y-coordinate plane. The x-axis runs from 0 to 10. The y-axis runs from 0 to 10. The half-line starts at the point (1, 0) and goes through the points (2, 1) and (5, 2).$

143.
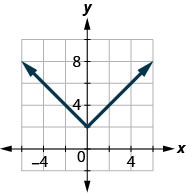
$The figure has an absolute value function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The vertex is at the point (0, 2). The line goes through the points (negative 1, 3) and (1, 3).$

Answer: $D: (-\inf ,\inf ), R: [2,\inf )$

144.
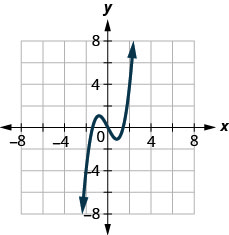
$The figure has a cubic function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The curved line goes through the points (negative 2, negative 4), (0, 0), and (2, 4).$

In the following exercises, use the graph of the function to find the indicated values.

145.
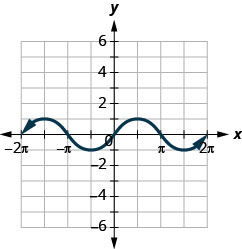
$This figure has a wavy curved line graphed on the x y-coordinate plane. The x-axis runs from negative 2 times pi to 2 times pi. The y-axis runs from negative 6 to 6. The curved line segment goes through the points (negative 2 times pi, 0), (negative 3 divided by 2 times pi, 1), (negative pi, 0), (negative 1 divided by 2 times pi, negative 1), (0, 0), (1 divided by 2 times pi, 1), (pi, 0), (3 divided by 2 times pi, negative 1), and (2 times pi, 0). The points (negative 3 divided by 2 times pi, 1) and (1 divided by 2 times pi, 1) are the highest points on the graph. The points (negative 1 divided by 2 times pi, negative 1) and (3 divided by 2 times pi, negative 1) are the lowest points on the graph. The pattern extends infinitely to the left and right.$

ⓐ Find $f(0)$.
ⓑ Find $f(12\pi )$.
ⓒ Find $f(−32\pi )$.
ⓓ Find the values for $x$ when $f(x)=0$.
ⓔ Find the $x$-intercepts.
ⓕ Find the $y$-intercept(s).
ⓖ Find the domain. Write it in interval notation.
ⓗ Find the range. Write it in interval notation.

Answer: ⓐ $f(x)=0$ ⓑ $f(\pi /2)=1$
ⓒ $f(−3\pi /2)=1$ ⓓ $f(x)=0$ for $x=−2\pi ,−\pi ,0,\pi ,2\pi$
ⓔ $(−2\pi ,0), (−\pi ,0), (0,0), (\pi ,0), (2\pi ,0)$ ⓕ $(0,0)$
ⓖ $[−2\pi ,2\pi ]$ ⓗ $[−1,1]$

146.
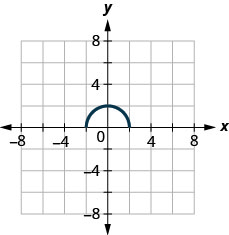
$The figure has a half-circle graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The curved line segment starts at the point (negative 2, 0). The line goes through the point (0, 2) and ends at the point (2, 0). The point (0, 2) is the highest point on the graph.$

ⓐ Find $f(0)$.
ⓑ Find the values for $x$ when $f(x)=0$.
ⓒ Find the $x$-intercepts.
ⓓ Find the $y$-intercept(s).
ⓔ Find the domain. Write it in interval notation.
ⓕ Find the range. Write it in interval notation.

Practice Test

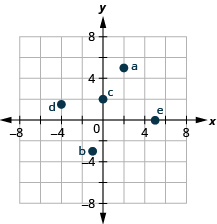
1. Plot each point in a rectangular coordinate system.

Answer: $This figure shows points plotted on the x y-coordinate plane. The x and y axes run from negative 10 to 10. The point labeled a is 2 units to the right of the origin and 5 units above the origin and is located in quadrant I. The point labeled b is 1 unit to the left of the origin and 3 units below the origin and is located in quadrant III. The point labeled c is 2 units above the origin and is located on the y-axis. The point labeled d is 4 units to the left of the origin and 1.5 units above the origin and is located in quadrant II. The point labeled e is 5 units to the right of the origin and is located on the x-axis.$

2. Which of the given ordered pairs are solutions to the equation $3x−y=6$?

3. Find the slope of each line shown.

ⓐ

ⓑ

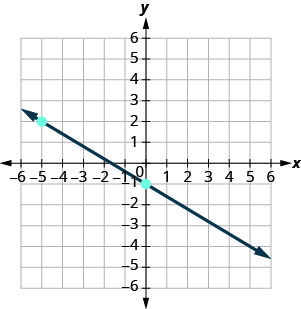
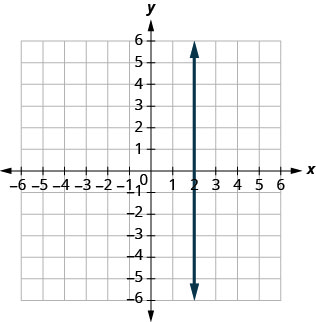
$The figure has a straight vertical line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (2, 0) (2, negative 1), and (2, 1).$

Answer: ⓐ $−\frac{3}{5}$ ⓑ undefined

4. Find the slope of the line between the points $(5,2)$ and $(−1,−4)$.

5. Graph the line with slope $\frac{1}{2}$ containing the point $(−3,−4)$.

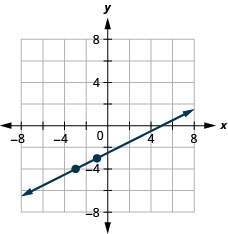
Answer: $The figure has a straight line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (negative 3, negative 4) (negative 1, negative 3), and (1, negative 2).$

6. Find the intercepts of $4x+2y=−8$ and graph.

Graph the line for each of the following equations.

7. $y=\frac{5}{3}x−1$

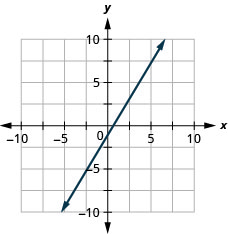
Answer: $The figure has a straight line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (negative 3, negative 6) (0, negative 1), and (3, 4).$

8. $y=−x$

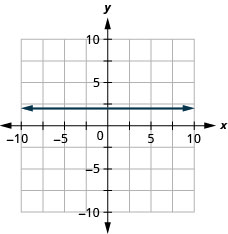
9. $y=2$

Answer: $The figure has a straight horizontal line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (negative 1, 2) (0, 2), and (1, 2).$

Find the equation of each line. Write the equation in slope-intercept form.

10. slope $−\frac{3}{4}$ and $y$-intercept $(0,−2)$

11. $m=2$, point $(−3,−1)$

Answer: $y=2x+5$

12. containing $(10,1)$ and $(6,−1)$

13. perpendicular to the line $y=\frac{5}{4}x+2$, containing the point $(−10,3)$

Answer: $y=−\frac{4}{5}x−5$

14. Write the inequality shown by the graph with the boundary line $y=−x−3$.

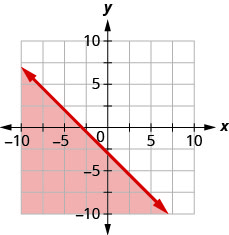
$The figure has a straight line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (negative 3, 0), (0, negative 3), and (1, negative 4). The line divides the coordinate plane into two halves. The bottom left half and the line are colored red to indicate that this is the solution set.$

Graph each linear inequality.

15. $y>\frac{3}{2}x+5$

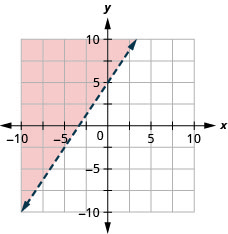
Answer: $The figure has a straight dashed line graphed on the x y-coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The line goes through the points (negative 2, 2), (0, 5), and (2, 8). The line divides the coordinate plane into two halves. The top left half is colored red to indicate that this is the solution set.$

16. $x−y\geq −4$

17. $y\leq −5x$

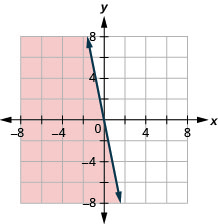
Answer: $The figure has a straight line graphed on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (negative 1, 5), (0, 0), and (1, negative 5). The line divides the coordinate plane into two halves. The bottom left half and the line are colored red to indicate that this is the solution set.$

18. Hiro works two part time jobs in order to earn enough money to meet her obligations of at least $450 a week. Her job at the mall pays $10 an hour and her administrative assistant job on campus pays $15 an hour. How many hours does Hiro need to work at each job to earn at least $450?

ⓐ Let x be the number of hours she works at the mall and let y be the number of hours she works as administrative assistant. Write an inequality that would model this situation.
ⓑ Graph the inequality .
ⓒ Find three ordered pairs $(x,y)$ that would be solutions to the inequality. Then explain what that means for Hiro.

19. Use the set of ordered pairs to ⓐ determine whether the relation is a function, ⓑ find the domain of the relation, and ⓒfind the range of the relation.

${\{(−3,27),(−2,8),(−1,1),(0,0),
(1,1),(2,8),(3,27)}\}$

$f(x)=4x^2−2x−3$

21. For $h(y)=3|y−1|−3$, evaluate $h(−4)$.

Answer: $12$

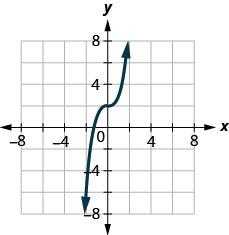
22. Determine whether the graph is the graph of a function. Explain your answer.

$The figure has a cube function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The curved line goes through the points (negative 1, 1), (0, 2), and (1, 3).$

In the following exercises, ⓐ graph each function ⓑ state its domain and range.
Write the domain and range in interval notation.

23. $f(x)=x^2+1$

Answer

ⓐ

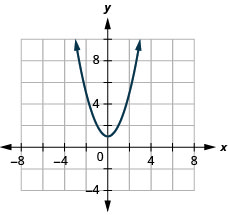
$The figure has a square function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The parabola goes through the points (negative 2, 5), (negative 1, 2), (0, 1), (1, 2), and (2, 5). The lowest point on the graph is (0, 1).$

ⓑ $D: (-\inf ,\inf ), R: [1,\inf )$

24. $f(x)=\sqrt{x+1}$

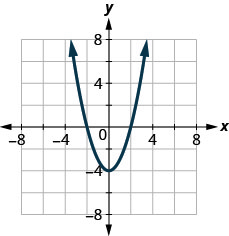
$The figure has a square function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The parabola goes through the points (negative 2, 0), (negative 1, negative 3), (0, negative 4), (1, negative 3), and (2, 0). The lowest point on the graph is (0, negative 4).$

ⓑ Find the $y$-intercepts.
ⓒ Find $f(−1)$.
ⓓ Find $f(1)$.
ⓔ Find the domain. Write it in interval notation.
ⓕ Find the range. Write it in interval notation.

Search

Text Color

Text Size

Margin Size

Font Type