3.7E: Exercises

Last updated
Save as PDF

Page ID: 30306

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Use the Vertical Line Test

In the following exercises, determine whether each graph is the graph of a function.

1. ⓐ

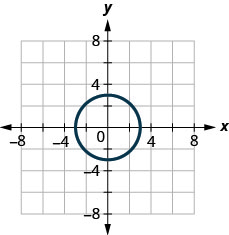
$The figure has a circle graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The circle goes through the points (negative 3, 0), (3, 0), (0, negative 3), and (0, 3).$

ⓑ

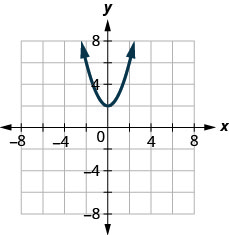
$The figure has a parabola opening up graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 4 to 8. The parabola goes through the points (negative 2, 6), (1, 3), (0, 2), (1, 3), and (2, 6).$

Answer: ⓐ no ⓑ yes

2. ⓐ

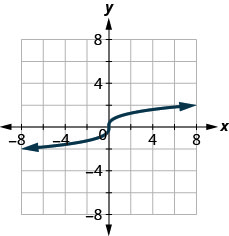
$The figure has an s-shaped curved line graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The s-shaped curved line goes through the points (negative 1, 1), (0, 0), and (1, 1).$

ⓑ

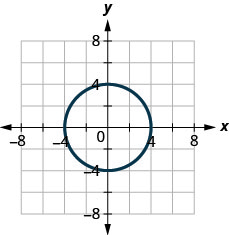
$The figure has a circle graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The circle goes through the points (negative 4, 0), (4, 0), (0, negative 4), and (0, 4).$

3. ⓐ

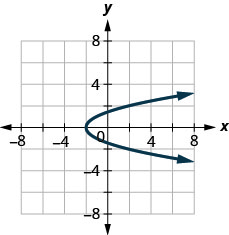
$The figure has a parabola opening right graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The parabola goes through the points (negative 2, 0), (negative 1, 1), (negative 1, negative 1), (negative 2, 2), and (2, 2).$

ⓑ

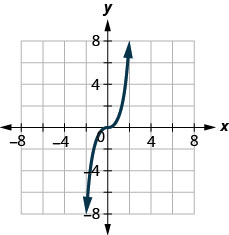
$The figure has a cube function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The curved line goes through the points (negative 1, negative 1), (0, 0), and (1, 1).$

Answer: ⓐ no ⓑ yes

4. ⓐ

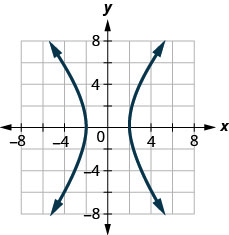
$The figure has two curved lines graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The curved line on the left goes through the points (negative 2, 0), (negative 4, 5), and (negative 4, negative 5). The curved line on the right goes through the points (2, 0), (4, 5), and (4, negative 5).$

ⓑ

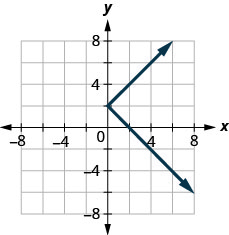
$The figure has a sideways absolute value function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line bends at the point (0, 2) and goes to the right. The line goes through the points (1, 3), (2, 4), (1, 1), and (2, 0).$

Identify Graphs of Basic Functions

In the following exercises, ⓐ graph each function ⓑ state its domain and range. Write the domain and range in interval notation.

5. $f(x)=3x+4$

Answer

ⓐ

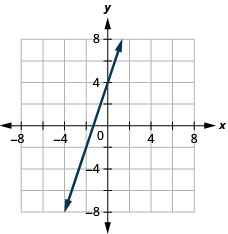
$The figure has a linear function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (negative 2, negative 2), (negative 1, 1), and (0, 4).$

ⓑ $ D:(-\inf ,\inf ),\space R:(-\inf ,\inf ) $

6. $f(x)=2x+5$

7. $f(x)=−x−2$

Answer

ⓐ

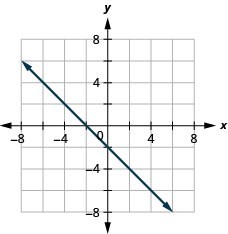
ⓑ $D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

8. $f(x)=−4x−3$

9. $f(x)=−2x+2$

Answer

ⓐ

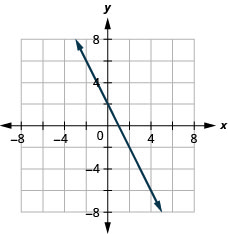
ⓑ $D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

10. $f(x)=−3x+3$

11. $f(x)=\frac{1}{2}x+1$

Answer

ⓐ

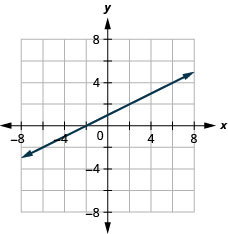
ⓑ $D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

12. $f(x)=\frac{2}{3}x−2$

13. $f(x)=5$

Answer

ⓐ

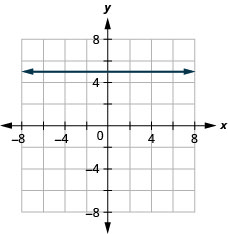
$The figure has a constant function graphed on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (negative 2, 5), (negative 1, 5), and (0, 5).$

ⓑ $D:(-\inf ,\inf ), R:{5}$

14. $f(x)=2$

15. $f(x)=−3$

Answer

ⓐ

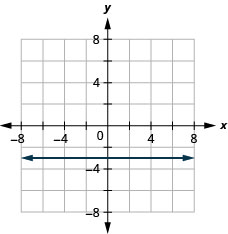
$The figure has a constant function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The line goes through the points (0, negative 3), (1, negative 3), and (2, negative 3).$

ⓑ $D:(-\inf ,\inf ),\space R: {−3}$

16. $f(x)=−1$

17. $f(x)=2x$

Answer

ⓐ

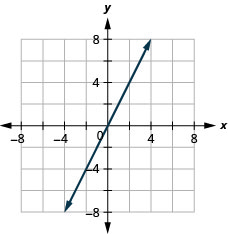
$The figure has a linear function graphed on the x y-coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. The line goes through the points (0, 0), (2, 4), and (negative 2, negative 4).$

ⓑ $D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

18. $f(x)=3x$

19. $f(x)=−2x$

Answer

ⓐ

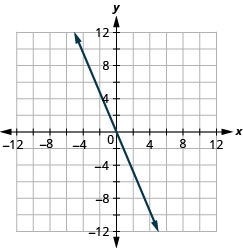
$The figure has a linear function graphed on the x y-coordinate plane. The x-axis runs from negative 12 to 12. The y-axis runs from negative 12 to 12. The line goes through the points (0, 0), (1, negative 2), and (negative 1, 2).$

ⓑ $D:(-\inf ,\inf ), R:(-\inf ,\inf )$

20. $f(x)=−3x$

21. $f(x)=3x^2$

Answer

ⓐ

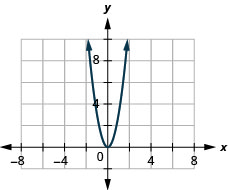
$The figure has a square function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The parabola goes through the points (negative 1, 3), (0, 0), and (1, 3). The lowest point on the graph is (0, 0).$

ⓑ $D:(-\inf ,\inf ),\space R:[0,\inf )$

22. $f(x)=2x^2$

23. $f(x)=−3x^2$

Answer

ⓐ

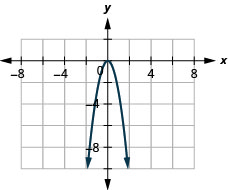
$The figure has a square function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 10 to 2. The parabola goes through the points (negative 1, negative 3), (0, 0), and (1, negative 3). The highest point on the graph is (0, 0).$

ⓑ $ D: (-\inf ,\inf ),\space R:(-\inf ,0]$

24. $f(x)=−2x^2$

25. $f(x)=12x^2$

Answer

ⓐ

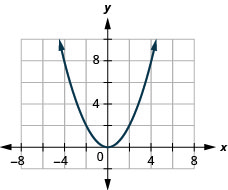
$The figure has a square function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The parabola goes through the points (negative 4, 8), (negative 2, 2), (0, 0), (2, 2), and (4, 8). The lowest point on the graph is (0, 0).$

ⓑ $D: (-\inf ,\inf ),\space R:[-\inf ,0)$

26. $f(x)=\frac{1}{3}x^2$

27. $f(x)=x^2−1$

Answer

ⓐ

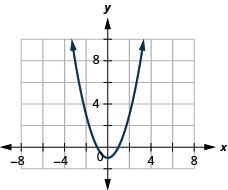
$The figure has a square function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The parabola goes through the points (negative 2, 3), (negative 1, 0), (0, negative 1), (1, 0), and (2, 3). The lowest point on the graph is (0, negative 1).$

ⓑ $D: (-\inf ,\inf ),\space R:[−1, \inf )$

28. $f(x)=x^2+1$

29. $f(x)=−2x^3$

Answer

ⓐ

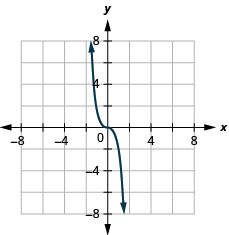
ⓑ $D:(-\inf ,\inf ),\space R:(-\inf ,\inf )$

30. $f(x)=2x^3$

31. $f(x)=x^3+2$

Answer

ⓐ

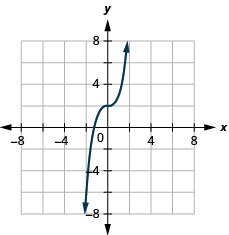
ⓑ $D:(-\inf ,\inf ), R:(-\inf ,\inf )$

32. $f(x)=x^3−2$

33. $f(x)=2\sqrt{x}$

Answer

ⓐ

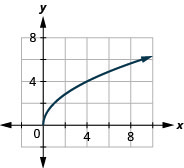
$The figure has a square root function graphed on the x y-coordinate plane. The x-axis runs from 0 to 10. The y-axis runs from 0 to 10. The half-line starts at the point (0, 0) and goes through the points (1, 2) and (4, 4).$

ⓑ $D:[0,\inf ), R:[0,\inf )$

34. $f(x)=−2\sqrt{x}$

35. $f(x)=\sqrt{x-1}$

Answer

ⓐ

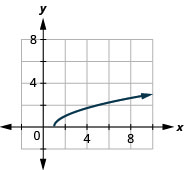
$The figure has a square root function graphed on the x y-coordinate plane. The x-axis runs from 0 to 10. The y-axis runs from 0 to 10. The half-line starts at the point (1, 0) and goes through the points (2, 1) and (5, 2).$

ⓑ $D:[1,\inf ), R:[0,\inf )$

36. $f(x)=\sqrt{x+1}$

37. $f(x)=3|x|$

Answer

ⓐ

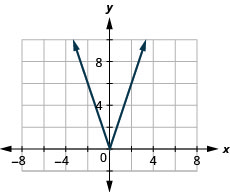
$The figure has an absolute value function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The vertex is at the point (0, 0). The line goes through the points (negative 1, 3) and (1, 3).$

ⓑ $D:[ −1,−1, \inf ), R:[−\inf ,\inf )$

38. $f(x)=−2|x|$

39. $f(x)=|x|+1$

Answer

ⓐ

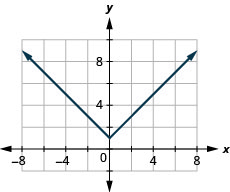
$The figure has an absolute value function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The vertex is at the point (0, 1). The line goes through the points (negative 1, 2) and (1, 2).$

ⓑ $D:(-\inf ,\inf ), R:[1,\inf )$

40. $f(x)=|x|−1$

Read Information from a Graph of a Function

In the following exercises, use the graph of the function to find its domain and range. Write the domain and range in interval notation.

41.
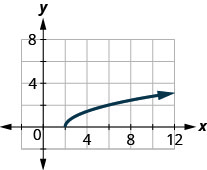
$The figure has a square root function graphed on the x y-coordinate plane. The x-axis runs from negative 2 to 8. The y-axis runs from negative 2 to 8. The half-line starts at the point (2, 0) and goes through the points (3, 1) and (6, 2).$

Answer: $D: [2,\inf ),\space R: [0,\inf )$

42.
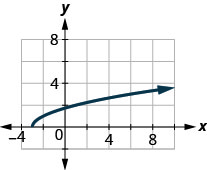
$The figure has a square root function graphed on the x y-coordinate plane. The x-axis runs from negative 2 to 8. The y-axis runs from negative 2 to 10. The half-line starts at the point (negative 3, 0) and goes through the points (negative 2, 1) and (1, 2).$

43.
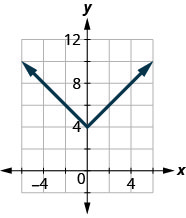
$The figure has an absolute value function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from 0 to 12. The vertex is at the point (0, 4). The line goes through the points (negative 2, 6) and (2, 6).$

Answer: $D: (-\inf ,\inf ),\space R: [4,\inf )$

44.
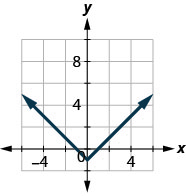
$The figure has an absolute value function graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 4 to 8. The vertex is at the point (0, negative 1). The line goes through the points (negative 1, 0) and (1, 0).$

45.
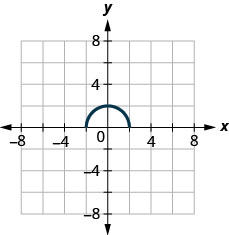
$The figure has a half-circle graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The curved line segment starts at the point (negative 2, 0). The line goes through the point (0, 2) and ends at the point (2, 0).$

Answer: $D: [−2,2],\space R: [0, 2]$

46.
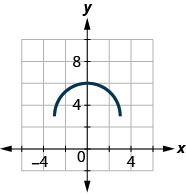
$The figure has a half-circle graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 2 to 10. The curved line segment starts at the point (negative 3, 3). The line goes through the point (0, 6) and ends at the point (3, 3).$

In the following exercises, use the graph of the function to find the indicated values.

47.
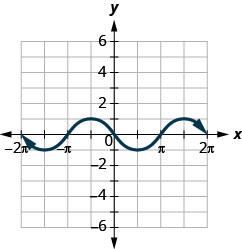
$This figure has a wavy curved line graphed on the x y-coordinate plane. The x-axis runs from negative 2 times pi to 2 times pi. The y-axis runs from negative 6 to 6. The curved line segment goes through the points (negative 2 times pi, 0), (negative 3 divided by 2 times pi, negative 1), (negative pi, 0), (negative 1 divided by 2 times pi, 1), (0, 0), (1 divided by 2 times pi, negative 1), (pi, 0), (3 divided by 2 times pi, 1), and (2 times pi, 0). The points (negative 3 divided by 2 times pi, negative 1) and (1 divided by 2 times pi, negative 1) are the lowest points on the graph. The points (negative 1 divided by 2 times pi, 1) and (3 divided by 2 times pi, 1) are the highest points on the graph. The pattern extends infinitely to the left and right.$

ⓐ Find: $f(0)$.
ⓑ Find: $f(12\pi)$.
ⓒ Find: $f(−32\pi)$.
ⓓ Find the values for $x$ when $f(x)=0$.
ⓔ Find the $x$-intercepts.
ⓕ Find the $y$-intercepts.
ⓖ Find the domain. Write it in interval notation.
ⓗ Find the range. Write it in interval notation.

Answer: ⓐ $f(0)=0$ ⓑ $(\pi/2)=−1$
ⓒ $f(−3\pi/2)=−1$ ⓓ $f(x)=0$ for $x=−2\pi,-\pi,0,\pi,2\pi$
ⓔ $(−2\pi,0),(−\pi,0),$ $(0,0),(\pi,0),(2\pi,0)$ $(f)(0,0)$
ⓖ $[−2\pi,2\pi]$ ⓗ $[−1,1]$

48.
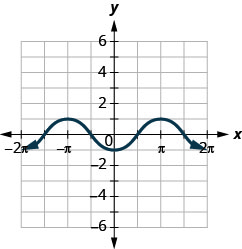
$Int_Alg_Section03_07_Exercise_48.jpeg$

ⓐ Find: $f(0)$.
ⓑ Find: $f(\pi)$.
ⓒ Find: $f(−\pi)$.
ⓓ Find the values for $x$ when $f(x)=0$.
ⓔ Find the $x$-intercepts.
ⓕ Find the $y$-intercepts.
ⓖ Find the domain. Write it in interval notation.
ⓗ Find the range. Write it in interval notation

49.
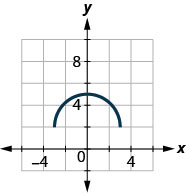
$The figure has the top half of a circle graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 4 to 8. The curved line segment starts at the point (negative 3, 2). The line goes through the point (0, 5) and ends at the point (3, 2). The point (0, 5) is the highest point on the graph. The points (negative 3, 2) and (3, 2) are the lowest points on the graph.$

ⓐ Find: $f(0)$.
ⓑ Find: $f(−3)$.
ⓒ Find: $f(3)$.
ⓓ Find the values for $x$ when $f(x)=0$.
ⓔ Find the $x$-intercepts.
ⓕ Find the $y$-intercepts.
ⓖ Find the domain. Write it in interval notation.
ⓗ Find the range. Write it in interval notation.

50.
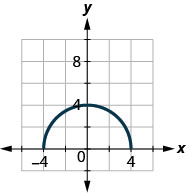
$The figure has the top half of a circle graphed on the x y-coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 4 to 8. The curved line segment starts at the point (negative 4, 0). The line goes through the point (0, 4) and ends at the point (4, 0). The point (0, 4) is the highest point on the graph. The points (negative 4, 0) and (4, 0) are the lowest points on the graph.$

ⓐ Find: $f(0)$.
ⓑ Find the values for $x$ when $f(x)=0$.
ⓒ Find the $x$-intercepts.
ⓓ Find the $y$-intercepts.
ⓔ Find the domain. Write it in interval notation.
ⓕ Find the range. Write it in interval notation

Writing Exercises

51. Explain in your own words how to find the domain from a graph.

52. Explain in your own words how to find the range from a graph.

53. Explain in your own words how to use the vertical line test.

54. Draw a sketch of the square and cube functions. What are the similarities and differences in the graphs?

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

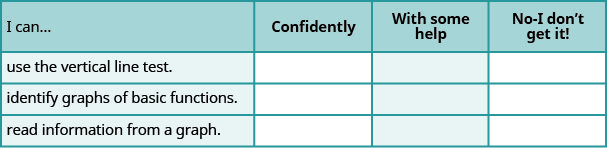
$The figure shows a table with four rows and four columns. The first row is a header row and it labels each column. The first column header is “I can…”, the second is "confidently", the third is “with some help”, “no minus I don’t get it!”. Under the first column are the phrases “use the vertical line test”, “identify graphs of basic functions”, and “read information from a graph”. Under the second, third, fourth columns are blank spaces where the learner can check what level of mastery they have achieved$

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

Search

Text Color

Text Size

Margin Size

Font Type