6.5: General Strategy for Factoring Polynomial Expressions
- Page ID
- 5156
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Recognize and use the appropriate method to factor a polynomial completely
Recognize and Use the Appropriate Method to Factor a Polynomial Completely
You have now become acquainted with all the methods of factoring that you will need in this course. The following chart summarizes all the factoring methods we have covered, and outlines a strategy you should use when factoring polynomials.
- Is there a greatest common factor?
Factor it out. - Is the polynomial a binomial, trinomial, or are there more than three terms?
If it is a binomial:- Is it a sum?
Of squares? Sums of squares do not factor.
Of cubes? Use the sum of cubes pattern. - Is it a difference?
Of squares? Factor as the product of conjugates.
Of cubes? Use the difference of cubes pattern.
- Is it of the form \(x^2+bx+c\)? Undo FOIL.
- Is it of the form \(ax^2+bx+c\)?
If a and c are squares, check if it fits the trinomial square pattern.
Use the trial and error or “\(ac\)” method.
- Use the grouping method.
- Is it a sum?
- Check.
Is it factored completely?
Do the factors multiply back to the original polynomial?
Remember, a polynomial is completely factored if, other than monomials, its factors are prime!
Factor completely: \(7x^3−21x^2−70x\).
Solution
\(\begin{array} {ll} {7x^3−21x^2−70x} & \\ \text{Is there a GCF? Yes, }7x. & \\ \text{Factor out the GCF.} &7x(x^2−3x−10) \\ \text{In the parentheses, is it a binomial, trinomial,} & \\ \text{or are there more terms?} & \\ \text{Trinomial with leading coefficient 1.} & \\ \text{“Undo” FOIL.} &7x(x\hspace{8mm})(x\hspace{8mm}) \\ &7x(x+2)(x−5) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Neither binomial can be factored.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ & \\ & \\ \hspace{15mm}7x(x+2)(x−5) & \\ \hspace{10mm}7x(x^2−5x+2x−10) & \\ \hspace{15mm}7x(x^2−3x−10) & \\ \hspace{13mm}7x^3−21x^2−70x\checkmark & \end{array} \)
Factor completely: \(8y^3+16y^2−24y\).
- Answer
-
\(8y(y−1)(y+3)\)
Factor completely: \(5y^3−15y^2−270y\).
- Answer
-
\(5y(y−9)(y+6)\)
Be careful when you are asked to factor a binomial as there are several options!
Factor completely: \(24y^2−150\)
Solution
\(\begin{array} {ll} &24y^2−150 \\ \text{Is there a GCF? Yes, }6. & \\ \text{Factor out the GCF.} &6(4y^2−25) \\ \text{In the parentheses, is it a binomial, trinomial} & \\ \text{or are there more than three terms? Binomial.} & \\ \text{Is it a sum? No.} & \\ \text{Is it a difference? Of squares or cubes? Yes, squares.} &6((2y)^2−(5)^2) \\ \text{Write as a product of conjugates.} &6(2y−5)(2y+5) \\ & \\ & \\ \hspace{5mm}\text{Is the expression factored completely?} & \\ \hspace{5mm}\text{Neither binomial can be factored.} & \\ \text{Check:} & \\ & \\ & \\ \hspace{5mm}\text{Multiply.} & \\ & \\ \hspace{15mm}6(2y−5)(2y+5) & \\ & \\ \hspace{18mm}6(4y^2−25) & \\ \hspace{18mm}24y^2−150\checkmark \end{array}\)
Factor completely: \(16x^3−36x\).
- Answer
-
\(4x(2x−3)(2x+3)\)
Factor completely: \(27y^2−48\).
- Answer
-
\(3(3y−4)(3y+4)\)
The next example can be factored using several methods. Recognizing the trinomial squares pattern will make your work easier.
Factor completely: \(4a^2−12ab+9b^2\).
Solution
\(\begin{array} {ll} &4a^2−12ab+9b^2 \\ \text{Is there a GCF? No.} & \\ \text{Is it a binomial, trinomial, or are there more terms?} & \\ \text{Trinomial with }a\neq 1.\text{ But the first term is a perfect square.} \\ \text{Is the last term a perfect square? Yes.} &(2a)^2−12ab+(3b)^2 \\ \text{Does it fit the pattern, }a^2−2ab+b^2?\text{ Yes.} &(2a)^2 −12ab+ (3b)^2 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(2a)(3b)}{\,}^{\swarrow}\\ \text{Write it as a square.} &(2a−3b)^2 \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \quad\text{The binomial cannot be factored.} & \\ \text{Check your answer.} \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{30mm}(2a−3b)^2 \\ \hspace{20mm} (2a)^2−2·2a·3b+(3b)^2 \\ \hspace{24mm}4a^2−12ab+9b^2\checkmark & \end{array} \)
Factor completely: \(4x^2+20xy+25y^2\).
- Answer
-
\((2x+5y)^2\)
Factor completely: \(9x^2−24xy+16y^2\).
- Answer
-
\((3x−4y)^2\)
Remember, sums of squares do not factor, but sums of cubes do!
Factor completely \(12x^3y^2+75xy^2\).
Solution
\(\begin{array} {ll} &12x^3y^2+75xy^2 \\ \text{Is there a GCF? Yes, }3xy^2. & \\ \text{Factor out the GCF.} &3xy^2(4x^2+25) \\ \text{In the parentheses, is it a binomial, trinomial, or are} & \\ \text{there more than three terms? Binomial.} & \\ & \\ \text{Is it a sum? Of squares? Yes.} &\text{Sums of squares are prime.} \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \text{Check:} & \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{15mm}3xy^2(4x^2+25) & \\ \hspace{14mm}12x^3y^2+75xy^2\checkmark \end{array} \)
Factor completely: \(50x^3y+72xy\).
- Answer
-
\(2xy(25x^2+36)\)
Factor completely: \(27xy^3+48xy\).
- Answer
-
\(3xy(9y^2+16)\)
When using the sum or difference of cubes pattern, being careful with the signs.
Factor completely: \(24x^3+81y^3\).
Solution
| Is there a GCF? Yes, 3. |  |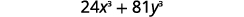
| Factor it out. |  |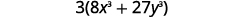
| In the parentheses, is it a binomial, trinomial, of are there more than three terms? Binomial. |
|
| Is it a sum or difference? Sum. | |
| Of squares or cubes? Sum of cubes. |  |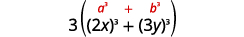
| Write it using the sum of cubes pattern. |  |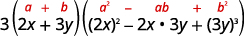
| Is the expression factored completely? Yes. |  |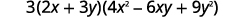
| Check by multiplying. |
Factor completely: \(250m^3+432n^3\).
- Answer
-
\(2(5m+6n)(25m^2−30mn+36n^2)\)
Factor completely: \(2p^3+54q^3\).
- Answer
-
\(2(p+3q)(p^2−3pq+9q^2)\)
Factor completely: \(3x^5y−48xy\).
Solution
\(\begin{array} {ll} &3x^5y−48xy \\ \text{Is there a GCF? Factor out }3xy &3xy(x^4−16) \\ \begin{array} {l} \text{Is the binomial a sum or difference? Of squares or cubes?} \\ \text{Write it as a difference of squares.} \end{array} &3xy\left((x^2)^2−(4)2\right) \\ \text{Factor it as a product of conjugates} &3xy(x^2−4)(x^2+4) \\ \text{The first binomial is again a difference of squares.} &3xy\left((x)^2−(2)^2\right)(x^2+4) \\ \text{Factor it as a product of conjugates.} &3xy(x−2)(x+2)(x^2+4) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ 3xy(x−2)(x+2)(x^2+4) & \\ 3xy(x^2−4)(x^2+4) & \\ 3xy(x^4−16) & \\ 3x^5y−48xy\checkmark & \end{array}\)
Factor completely: \(4a^5b−64ab\).
- Answer
-
\(4ab(a^2+4)(a−2)(a+2)\)
Factor completely: \(7xy^5−7xy\).
- Answer
-
\(7xy(y^2+1)(y−1)(y+1)\)
Factor completely: \(4x^2+8bx−4ax−8ab\).
Solution
\(\begin{array} {ll} &4x^2+8bx−4ax−8ab \\ \text{Is there a GCF? Factor out the GCF, }4. &4(x^2+2bx−ax−2ab) \\ \text{There are four terms. Use grouping.} &4[x(x+2b)−a(x+2b)]4(x+2b)(x−a) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4(x+2b)(x−a) & \\ \hspace{20mm} 4(x^2−ax+2bx−2ab) & \\ \hspace{20mm}4x^2+8bx−4ax−8ab\checkmark \end{array}\)
Factor completely: \(6x^2−12xc+6bx−12bc\).
- Answer
-
\(6(x+b)(x−2c)\)
Factor completely: \(16x^2+24xy−4x−6y\).
- Answer
-
\(2(4x−1)(2x+3y)\)
Taking out the complete GCF in the first step will always make your work easier.
Factor completely: \(40x^2y+44xy−24y\).
Solution
\(\begin{array} {ll} &40x^2y+44xy−24y \\ \text{Is there a GCF? Factor out the GCF, }4y. &4y(10x^2+11x−6) \\ \text{Factor the trinomial with }a\neq 1. &4y(10x^2+11x−6) \\ &4y(5x−2)(2x+3) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4y(5x−2)(2x+3) & \\ \hspace{24mm}4y(10x^2+11x−6) & \\ \hspace{22mm}40x^2y+44xy−24y\checkmark \end{array}\)
Factor completely: \(4p^2q−16pq+12q\).
- Answer
-
\(4q(p−3)(p−1)\)
Factor completely: \(6pq^2−9pq−6p\).
- Answer
-
\(3p(2q+1)(q−2)\)
When we have factored a polynomial with four terms, most often we separated it into two groups of two terms. Remember that we can also separate it into a trinomial and then one term.
Factor completely: \(9x^2−12xy+4y^2−49\).
Solution
\(\begin{array} {ll} &9x^2−12xy+4y^2−49 \\ \text{Is there a GCF? No.} & \\ \begin{array} {l} \text{With more than 3 terms, use grouping. Last 2 terms} \\ \text{have no GCF. Try grouping first 3 terms.} \end{array} &9x^2−12xy+4y^2−49 \\ \begin{array} {l} \text{Factor the trinomial with }a\neq 1. \text{ But the first term is a} \\ \text{perfect square.} \end{array} & \\ \text{Is the last term of the trinomial a perfect square? Yes.} &(3x)^2−12xy+(2y)^2−49 \\ \text{Does the trinomial fit the pattern, }a^2−2ab+b^2? \text{ Yes.} &(3x)^2 −12xy+ (2y)^2−49 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(3x)(2y))}{\,}^{\swarrow} \\ \text{Write the trinomial as a square.} &(3x−2y)^2−49 \\ \begin{array} {ll} \text{Is this binomial a sum or difference? Of squares or} \\ \text{cubes? Write it as a difference of squares.} \end{array} &(3x−2y)^2−72 \\ \text{Write it as a product of conjugates.} &((3x−2y)−7)((3x−2y)+7) \\ &(3x−2y−7)(3x−2y+7) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{23mm}(3x−2y−7)(3x−2y+7) & \\ \hspace{10mm}9x^2−6xy−21x−6xy+4y^2+14y+21x−14y−49 \qquad & \\ \hspace{25mm}9x^2−12xy+4y^2−49\checkmark & \end{array}\)
Factor completely: \(4x^2−12xy+9y^2−25\).
- Answer
-
\((2x−3y−5)(2x−3y+5)\)
Factor completely: \(16x^2−24xy+9y^2−64\).
- Answer
-
\((4x−3y−8)(4x−3y+8)\)
Key Concepts
- How to use a general strategy for factoring polynomials.
- Is there a greatest common factor?
Factor it out. - Is the polynomial a binomial, trinomial, or are there more than three terms?
If it is a binomial:
Is it a sum?
Of squares? Sums of squares do not factor.
Of cubes? Use the sum of cubes pattern.
Is it a difference?
Of squares? Factor as the product of conjugates.
Of cubes? Use the difference of cubes pattern.
If it is a trinomial:
Is it of the form \(x^2+bx+c\)? Undo FOIL.
Is it of the form \(ax^2+bx+c\)?
If a and c are squares, check if it fits the trinomial square pattern.
Use the trial and error or “\(ac\)” method.
If it has more than three terms:
Use the grouping method. - Check.
Is it factored completely?
Do the factors multiply back to the original polynomial?
- Is there a greatest common factor?