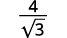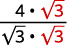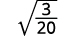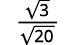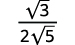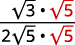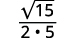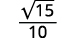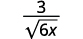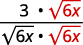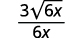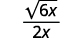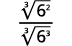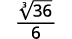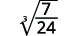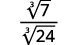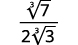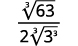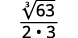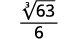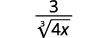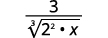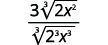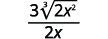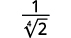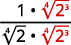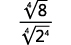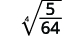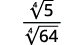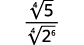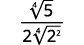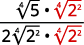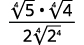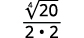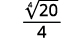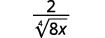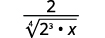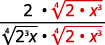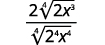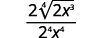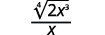8.6: Divide Radical Expressions
- Page ID
- 5171
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Divide radical expressions
- Rationalize a one term denominator
- Rationalize a two term denominator
Before you get started, take this readiness quiz.
- Simplify: \(\dfrac{30}{48}\).
If you missed this problem, review Example 1.24. - Simplify: \(x^{2}⋅x^{4}\).
If you missed this problem, review Example 5.12. - Multiply: \((7+3x)(7−3x)\).
If you missed this problem, review Example 5.32.
Divide Radical Expressions
We have used the Quotient Property of Radical Expressions to simplify roots of fractions. We will need to use this property ‘in reverse’ to simplify a fraction with radicals. We give the Quotient Property of Radical Expressions again for easy reference. Remember, we assume all variables are greater than or equal to zero so that no absolute value bars re needed.
Definition \(\PageIndex{1}\): Quotient Property of Radical Expressions
If \(\sqrt[n]{a}\) and \(\sqrt[n]{b}\) are real numbers, \(b≠0\), and for any integer \(n≥2\) then,
\(\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} \quad \text { and } \quad \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\)
We will use the Quotient Property of Radical Expressions when the fraction we start with is the quotient of two radicals, and neither radicand is a perfect power of the index. When we write the fraction in a single radical, we may find common factors in the numerator and denominator.
Simplify:
- \(\dfrac{\sqrt{72 x^{3}}}{\sqrt{162 x}}\)
- \(\dfrac{\sqrt[3]{32 x^{2}}}{\sqrt[3]{4 x^{5}}}\)
Solution:
a.
\(\dfrac{\sqrt{72 x^{3}}}{\sqrt{162 x}}\)
Rewrite using the quotient property,
\(\sqrt{\dfrac{72 x^{3}}{162 x}}\)
Remove common factors.
\(\sqrt{\dfrac{\cancel{18} \cdot 4 \cdot x^{2} \cdot \cancel{x}}{\cancel{18} \cdot 9 \cdot \cancel{x}}}\)
Simplify.
\(\sqrt{\dfrac{4 x^{2}}{9}}\)
Simplify the radical.
\(\dfrac{2 x}{3}\)
b.
\(\dfrac{\sqrt[3]{32 x^{2}}}{\sqrt[3]{4 x^{5}}}\)
Rewrite using the quotient property, \(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\).
\(\sqrt[3]{\dfrac{32 x^{2}}{4 x^{5}}}\)
Simplify the fraction under the radical.
\(\sqrt[3]{\dfrac{8}{x^{3}}}\)
Simplify the radical.
\(\dfrac{2}{x}\)
Simplify:
- \(\dfrac{\sqrt{50 s^{3}}}{\sqrt{128 s}}\)
- \(\dfrac{\sqrt[3]{56 a}}{\sqrt[3]{7 a^{4}}}\)
- Answer
-
- \(\dfrac{5s}{8}\)
- \(\dfrac{2}{a}\)
Simplify:
- \(\dfrac{\sqrt{75 q^{5}}}{\sqrt{108 q}}\)
- \(\dfrac{\sqrt[3]{72 b^{2}}}{\sqrt[3]{9 b^{5}}}\)
- Answer
-
- \(\dfrac{5 q^{2}}{6}\)
- \(\dfrac{2}{b}\)
Simplify:
- \(\dfrac{\sqrt{147 a b^{8}}}{\sqrt{3 a^{3} b^{4}}}\)
- \(\dfrac{\sqrt[3]{-250 m n^{-2}}}{\sqrt[3]{2 m^{-2} n^{4}}}\)
Solution:
a.
\(\dfrac{\sqrt{147 a b^{8}}}{\sqrt{3 a^{3} b^{4}}}\)
Rewrite using the quotient property.
\(\sqrt{\dfrac{147 a b^{8}}{3 a^{3} b^{4}}}\)
Remove common factors in the fraction.
\(\sqrt{\dfrac{49 b^{4}}{a^{2}}}\)
Simplify the radical.
\(\dfrac{7 b^{2}}{a}\)
b.
\(\dfrac{\sqrt[3]{-250 m n^{-2}}}{\sqrt[3]{2 m^{-2} n^{4}}}\)
Rewrite using the quotient property.
\(\sqrt[3]{\dfrac{-250 m n^{-2}}{2 m^{-2} n^{4}}}\)
Simplify the fraction under the radical.
\(\sqrt[3]{\dfrac{-125 m^{3}}{n^{6}}}\)
Simplify the radical.
\(-\dfrac{5 m}{n^{2}}\)
Simplify:
- \(\dfrac{\sqrt{162 x^{10} y^{2}}}{\sqrt{2 x^{6} y^{6}}}\)
- \(\dfrac{\sqrt[3]{-128 x^{2} y^{-1}}}{\sqrt[3]{2 x^{-1} y^{2}}}\)
- Answer
-
- \(\dfrac{9 x^{2}}{y^{2}}\)
- \(\dfrac{-4 x}{y}\)
Simplify:
- \(\dfrac{\sqrt{300 m^{3} n^{7}}}{\sqrt{3 m^{5} n}}\)
- \(\dfrac{\sqrt[3]{-81 p q^{-1}}}{\sqrt[3]{3 p^{-2} q^{5}}}\)
- Answer
-
- \(\dfrac{10 n^{3}}{m}\)
- \(\dfrac{-3 p}{q^{2}}\)
Simplify: \(\dfrac{\sqrt{54 x^{5} y^{3}}}{\sqrt{3 x^{2} y}}\)
Solution:
\(\dfrac{\sqrt{54 x^{5} y^{3}}}{\sqrt{3 x^{2} y}}\)
Rewrite using the quotient property.
\(\sqrt{\dfrac{54 x^{5} y^{3}}{3 x^{2} y}}\)
Remove common factors in the fraction.
\(\sqrt{18 x^{3} y^{2}}\)
Rewrite the radicand as a product using the largest perfect square factor.
\(\sqrt{9 x^{2} y^{2} \cdot 2 x}\)
Rewrite the radical as the product of two radicals.
\(\sqrt{9 x^{2} y^{2}} \cdot \sqrt{2 x}\)
Simplify.
\(3 x y \sqrt{2 x}\)
Simplify: \(\dfrac{\sqrt{64 x^{4} y^{5}}}{\sqrt{2 x y^{3}}}\)
- Answer
-
\(4 x y \sqrt{2 x}\)
Simplify: \(\dfrac{\sqrt{96 a^{5} b^{4}}}{\sqrt{2 a^{3} b}}\)
- Answer
-
\(4 a b \sqrt{3 b}\)
Rationalize a One Term Denominator
Before the calculator became a tool of everyday life, approximating the value of a fraction with a radical in the denominator was a very cumbersome process!
For this reason, a process called rationalizing the denominator was developed. A fraction with a radical in the denominator is converted to an equivalent fraction whose denominator is an integer. Square roots of numbers that are not perfect squares are irrational numbers. When we rationalize the denominator, we write an equivalent fraction with a rational number in the denominator. This process is still used today, and is useful in other areas of mathematics, too.
Definition \(\PageIndex{2}\): Rationalizing the Denominator
Rationalizing the denominator is the process of converting a fraction with a radical in the denominator to an equivalent fraction whose denominator is an integer.
Even though we have calculators available nearly everywhere, a fraction with a radical in the denominator still must be rationalized. It is not considered simplified if the denominator contains a radical.
Similarly, a radical expression is not considered simplified if the radicand contains a fraction.
Simplified Radical Expressions
A radical expression is considered simplified if there are
- no factors in the radicand have perfect powers of the index
- no fractions in the radicand
- no radicals in the denominator of a fraction
To rationalize a denominator with a square root, we use the property that \((\sqrt{a})^{2}=a\). If we square an irrational square root, we get a rational number.
We will use this property to rationalize the denominator in the next example.
Simplify:
- \(\dfrac{4}{\sqrt{3}}\)
- \(\sqrt{\dfrac{3}{20}}\)
- \(\dfrac{3}{\sqrt{6 x}}\)
Solution:
To rationalize a denominator with one term, we can multiply a square root by itself. To keep the fraction equivalent, we multiply both the numerator and denominator by the same factor.
a.
|
|
|
| Multiply both the numerator and denominator by \(\sqrt{3}\). |
|
| Simplify. |
|
b. We always simplify the radical in the denominator first, before we rationalize it. This way the numbers stay smaller and easier to work with.
|
|
|
| The fraction is not a perfect square, so rewrite using the Quotient Property. |
|
| Simplify the denominator. |
|
| Multiply the numerator and denominator by \(\sqrt{5}\). |
|
| Simplify. |
|
| Simplify. |
|
c.
|
|
|
| Multiply the numerator and denominator by \(\sqrt{6x}\). |
|
| Simplify. |
|
| Simplify. |
|
Simplify:
- \(\dfrac{5}{\sqrt{3}}\)
- \(\sqrt{\dfrac{3}{32}}\)
- \(\dfrac{2}{\sqrt{2 x}}\)
- Answer
-
- \(\dfrac{5 \sqrt{3}}{3}\)
- \(\dfrac{\sqrt{6}}{8}\)
- \(\dfrac{\sqrt{2 x}}{x}\)
Simplify:
- \(\dfrac{6}{\sqrt{5}}\)
- \(\sqrt{\dfrac{7}{18}}\)
- \(\dfrac{5}{\sqrt{5 x}}\)
- Answer
-
- \(\dfrac{6 \sqrt{5}}{5}\)
- \(\dfrac{\sqrt{14}}{6}\)
- \(\dfrac{\sqrt{5 x}}{x}\)
When we rationalized a square root, we multiplied the numerator and denominator by a square root that would give us a perfect square under the radical in the denominator. When we took the square root, the denominator no longer had a radical.
We will follow a similar process to rationalize higher roots. To rationalize a denominator with a higher index radical, we multiply the numerator and denominator by a radical that would give us a radicand that is a perfect power of the index. When we simplify the new radical, the denominator will no longer have a radical.
For example,
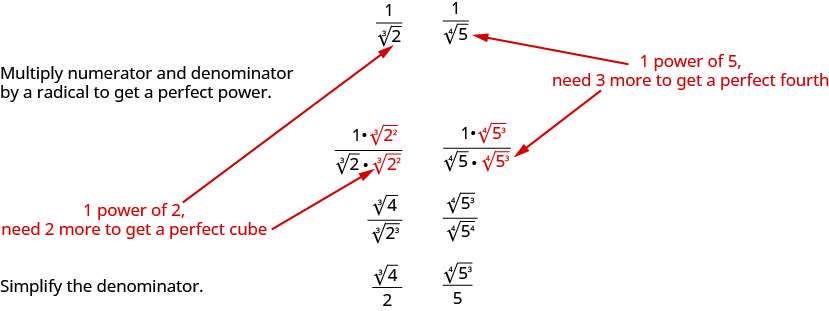
We will use this technique in the next examples.
Simplify:
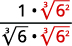
- \(\dfrac{1}{\sqrt[3]{6}}\)
- \(\sqrt[3]{\dfrac{7}{24}}\)
- \(\dfrac{3}{\sqrt[3]{4 x}}\)
Solution:
To rationalize a denominator with a cube root, we can multiply by a cube root that will give us a perfect cube in the radicand in the denominator. To keep the fraction equivalent, we multiply both the numerator and denominator by the same factor.
a.
|
|
|
| The radical in the denominator has one factor of \(6\). Multiply both the numerator and denominator by \(\sqrt[3]{6^{2}}\), which gives us \(2\) more factors of \(6\). |
|
| Multiply. Notice the radicand in the denominator has \(3\) powers of \(6\). |
|
| Simplify the cube root in the denominator. |
|
b. We always simplify the radical in the denominator first, before we rationalize it. This way the numbers stay smaller and easier to work with.
|
|
|
| The fraction is not a perfect cube, so rewrite using the Quotient Property. |
|
| Simplify the denominator. |
|
| Multiply the numerator and denominator by \(\sqrt[3]{3^{2}}\). This will give us \(3\) factors of \(3\). |
|
| Simplify. |
|
| Remember, \(\sqrt[3]{3^{3}}=3\). |
|
| Simplify. |
|
c.
|
|
|
| Rewrite the radicand to show the factors. |
|
| Multiple the numerator and denominator by \(\sqrt[3]{2 \cdot x^{2}}\). This will get us \(3\) factors of \(2\) and \(3\) factors of \(x\). |
|
| Simplify. |
|
| Simplify the radical in the denominator. |
|
Simplify:
- \(\dfrac{1}{\sqrt[3]{7}}\)
- \(\sqrt[3]{\dfrac{5}{12}}\)
- \(\dfrac{5}{\sqrt[3]{9 y}}\)
- Answer
-
- \(\dfrac{\sqrt[3]{49}}{7}\)
- \(\dfrac{\sqrt[3]{90}}{6}\)
- \(\dfrac{5 \sqrt[3]{3 y^{2}}}{3 y}\)
Simplify:
- \(\dfrac{1}{\sqrt[3]{2}}\)
- \(\sqrt[3]{\dfrac{3}{20}}\)
- \(\dfrac{2}{\sqrt[3]{25 n}}\)
- Answer
-
- \(\dfrac{\sqrt[3]{4}}{2}\)
- \(\dfrac{\sqrt[3]{150}}{10}\)
- \(\dfrac{2 \sqrt[3]{5 n^{2}}}{5 n}\)
Simplify:
- \(\dfrac{1}{\sqrt[4]{2}}\)
- \(\sqrt[4]{\dfrac{5}{64}}\)
- \(\dfrac{2}{\sqrt[4]{8 x}}\)
Solution:
To rationalize a denominator with a fourth root, we can multiply by a fourth root that will give us a perfect fourth power in the radicand in the denominator. To keep the fraction equivalent, we multiply both the numerator and denominator by the same factor.
a.
|
|
|
| The radical in the denominator has one factor of \(2\). Multiply both the numerator and denominator by \(\sqrt[4]{2^{3}}\), which gives us \(3\) more factors of \(2\). |
|
| Multiply. Notice the radicand in the denominator has \(4\) powers of \(2\). |
|
| Simplify the fourth root in the denominator. |
|
b. We always simplify the radical in the denominator first, before we rationalize it. This way the numbers stay smaller and easier to work with.
|
|
|
| The fraction is not a perfect fourth power, so rewrite using the Quotient Property. |
|
| Rewrite the radicand in the denominator to show the factors. |
|
| Simplify the denominator. |
|
| Multiply the numerator and denominator by \(\sqrt[4]{2^{2}}\). This will give us \(4\) factors of \(2\). |
|
| Simplify. |
|
| Remember, \(\sqrt[4]{2^{4}}=2\). |
|
| Simplify. |
|
c.
|
|
|
| Rewrite the radicand to show the factors. |
|
| Multiply the numerator and denominator by \(\sqrt[4]{2 \cdot x^{3}}\). This will get us \(4\) factors of \(2\) and \(4\) factors of \(x\). |
|
| Simplify. |
|
| Simplify the radical in the denominator. |
|
| Simplify the fraction. |
|
Simplify:
- \(\dfrac{1}{\sqrt[4]{3}}\)
- \(\sqrt[4]{\dfrac{3}{64}}\)
- \(\dfrac{3}{\sqrt[4]{125 x}}\)
- Answer
-
- \(\dfrac{\sqrt[4]{27}}{3}\)
- \(\dfrac{\sqrt[4]{12}}{4}\)
- \(\dfrac{3 \sqrt[4]{5 x^{3}}}{5 x}\)
Simplify:
- \(\dfrac{1}{\sqrt[4]{5}}\)
- \(\sqrt[4]{\dfrac{7}{128}}\)
- \(\dfrac{4}{\sqrt[4]{4 x}}\)
- Answer
-
- \(\dfrac{\sqrt[4]{125}}{5}\)
- \(\dfrac{\sqrt[4]{224}}{8}\)
- \(\dfrac{\sqrt[4]{64 x^{3}}}{x}\)
Rationalize a Two Term Denominator
When the denominator of a fraction is a sum or difference with square roots, we use the Product of Conjugates Pattern to rationalize the denominator.
\(\begin{array}{c c}{(a-b)(a+b)} & {(2-\sqrt{5})(2+\sqrt{5})} \\ {a^{2}-b^{2}} &{ 2^{2}-(\sqrt{5})^{2}} \\ {}&{4-5} \\ {}&{-1}\end{array}\)
When we multiple a binomial that includes a square root by its conjugate, the product has no square roots.
Simplify: \(\dfrac{5}{2-\sqrt{3}}\)
Solution:
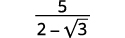 |
|
| Multiply the numerator and denominator by the conjugate of the denominator. |  |
| Multiply the conjugates in the denominator. | 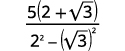 |
| Simplify the denominator. | 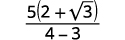 |
| Simplify the denominator. | 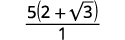 |
| Simplify. | 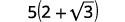 |
Simplify: \(\dfrac{3}{1-\sqrt{5}}\).
- Answer
-
\(-\dfrac{3(1+\sqrt{5})}{4}\)
Simplify: \(\dfrac{2}{4-\sqrt{6}}\).
- Answer
-
\(\dfrac{4+\sqrt{6}}{5}\)
Notice we did not distribute the \(5\) in the answer of the last example. By leaving the result factored we can see if there are any factors that may be common to both the numerator and denominator.
Simplify: \(\dfrac{\sqrt{3}}{\sqrt{u}-\sqrt{6}}\).
Solution:
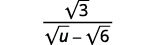 |
|
| Multiply the numerator and denominator by the conjugate of the denominator. | 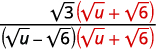 |
| Multiply the conjugates in the denominator. | 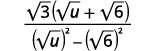 |
| Simplify the denominator. | 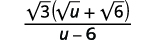 |
Simplify: \(\dfrac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).
- Answer
-
\(\dfrac{\sqrt{5}(\sqrt{x}-\sqrt{2})}{x-2}\)
Simplify: \(\dfrac{\sqrt{10}}{\sqrt{y}-\sqrt{3}}\)
- Answer
-
\(\dfrac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y-3}\)
Be careful of the signs when multiplying. The numerator and denominator look very similar when you multiply by the conjugate.
Simplify: \(\dfrac{\sqrt{x}+\sqrt{7}}{\sqrt{x}-\sqrt{7}}\).
Solution:
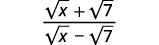 |
|
| Multiply the numerator and denominator by the conjugate of the denominator. |  |
| Multiply the conjugates in the denominator. | 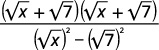 |
| Simplify the denominator. | 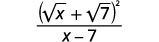 |
We do not square the numerator. Leaving it in factored form, we can see there are no common factors to remove from the numerator and denominator.
Simplify: \(\dfrac{\sqrt{p}+\sqrt{2}}{\sqrt{p}-\sqrt{2}}\).
- Answer
-
\(\dfrac{(\sqrt{p}+\sqrt{2})^{2}}{p-2}\)
Simplify: \(\dfrac{\sqrt{q}-\sqrt{10}}{\sqrt{q}+\sqrt{10}}\)
- Answer
-
\(\dfrac{(\sqrt{q}-\sqrt{10})^{2}}{q-10}\)
Key Concepts
- Quotient Property of Radical Expressions
- If \(\sqrt[n]{a}\) and \(\sqrt[n]{b}\) are real numbers, \(b≠0\), and for any integer \(n≥2\) then, \(\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\) and \(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\)
- Simplified Radical Expressions
- A radical expression is considered simplified if there are:
- no factors in the radicand that have perfect powers of the index
- no fractions in the radicand
- no radicals in the denominator of a fraction
- A radical expression is considered simplified if there are:
Glossary
- rationalizing the denominator
- Rationalizing the denominator is the process of converting a fraction with a radical in the denominator to an equivalent fraction whose denominator is an integer.