8.8E: Exercises

Last updated
Save as PDF

Page ID: 30332

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Exercise $\PageIndex{17}$ Evaluate a Radical Function

In the following exercises, evaluate each function.

$f(x)=\sqrt{4 x-4}$, find
1. $f(5)$
2. $f(0)$
$f(x)=\sqrt{6 x-5}$, find
1. $f(5)$
2. $f(-1)$
$g(x)=\sqrt{6 x+1}$, find
1. $g(4)$
2. $g(8)$
$g(x)=\sqrt{3 x+1}$, find
1. $g(8)$
2. $g(5)$
$F(x)=\sqrt{3-2 x}$, find
1. $F(1)$
2. $F(-11)$
$F(x)=\sqrt{8-4 x}$, find
1. $F(1)$
2. $F(-2)$
$G(x)=\sqrt{5 x-1}$, find
1. $G(5)$
2. $G(2)$
$G(x)=\sqrt{4 x+1}$, find
1. $G(11)$
2. $G(2)$
$g(x)=\sqrt[3]{2 x-4}$, find
1. $g(6)$
2. $g(-2)$
$g(x)=\sqrt[3]{7 x-1}$, find
1. $g(4)$
2. $g(-1)$
$h(x)=\sqrt[3]{x^{2}-4}$, find
1. $h(-2)$
2. $h(6)$
$h(x)=\sqrt[3]{x^{2}+4}$, find
1. $h(-2)$
2. $h(6)$
For the function $f(x)=\sqrt[4]{2 x^{3}}$, find
1. $f(0)$
2. $f(2)$
For the function $f(x)=\sqrt[4]{3 x^{3}}$, find
1. $f(0)$
2. $f(3)$
For the function $g(x)=\sqrt[4]{4-4 x}$, find
1. $g(1)$
2. $g(-3)$
For the function $g(x)=\sqrt[4]{8-4 x}$, find
1. $g(-6)$
2. $g(2)$

Answer

$f(5)=4$
no value at $x=0$

$g(4)=5$
$g(8)=7$

$F(1)=1$
$F(-11)=5$

$G(5)=2 \sqrt{6}$
$G(2)=3$

$g(6)=2$
$g(-2)=-2$

11.

$h(-2)=0$
$h(6)=2 \sqrt[3]{4}$

13.

$f(0)=0$
$f(2)=2$

15.

$g(1)=0$
$g(-3)=2$

Exercise $\PageIndex{18}$ Find the Domain of a Radical Function

In the following exercises, find the domain of the function and write the domain in interval notation.

$f(x)=\sqrt{3 x-1}$
$f(x)=\sqrt{4 x-2}$
$g(x)=\sqrt{2-3 x}$
$g(x)=\sqrt{8-x}$
$h(x)=\sqrt{\frac{5}{x-2}}$
$h(x)=\sqrt{\frac{6}{x+3}}$
$f(x)=\sqrt{\frac{x+3}{x-2}}$
$f(x)=\sqrt{\frac{x-1}{x+4}}$
$g(x)=\sqrt[3]{8 x-1}$
$g(x)=\sqrt[3]{6 x+5}$
$f(x)=\sqrt[3]{4 x^{2}-16}$
$f(x)=\sqrt[3]{6 x^{2}-25}$
$F(x)=\sqrt[4]{8 x+3}$
$F(x)=\sqrt[4]{10-7 x}$
$G(x)=\sqrt[5]{2 x-1}$
$G(x)=\sqrt[5]{6 x-3}$

Answer

1. $\left[\frac{1}{3}, \infty\right)$

3. $\left(-\infty, \frac{2}{3}\right]$

5. $(2, \infty)$

7. $(-\infty,-3] \cup(2, \infty)$

9. $(-\infty, \infty)$

11. $(-\infty, \infty)$

13. $\left[-\frac{3}{8}, \infty\right)$

15. $(-\infty, \infty)$

Exercise $\PageIndex{19}$ graph radical functions

In the following exercises,

find the domain of the function
graph the function
use the graph to determine the range
1. $f(x)=\sqrt{x+1}$
2. $f(x)=\sqrt{x-1}$
3. $g(x)=\sqrt{x+4}$
4. $g(x)=\sqrt{x-4}$
5. $f(x)=\sqrt{x}+2$
6. $f(x)=\sqrt{x}-2$
7. $g(x)=2 \sqrt{x}$
8. $g(x)=3 \sqrt{x}$
9. $f(x)=\sqrt{3-x}$
10. $f(x)=\sqrt{4-x}$
11. $g(x)=-\sqrt{x}$
12. $g(x)=-\sqrt{x}+1$
13. $f(x)=\sqrt[3]{x+1}$
14. $f(x)=\sqrt[3]{x-1}$
15. $g(x)=\sqrt[3]{x+2}$
16. $g(x)=\sqrt[3]{x-2}$
17. $f(x)=\sqrt[3]{x}+3$
18. $f(x)=\sqrt[3]{x}-3$
19. $g(x)=\sqrt[3]{x}$
20. $g(x)=-\sqrt[3]{x}$
21. $f(x)=2 \sqrt[3]{x}$
22. $f(x)=-2 \sqrt[3]{x}$

Answer

domain: $[-1, \infty)$
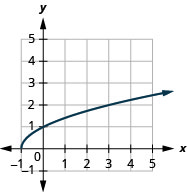
$The figure shows a square root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 1 to 7. The y-axis runs from negative 2 to 10. The function has a starting point at (negative 1, 0) and goes through the points (0, 1) and (3, 2).$
Figure 8.7.8
$[0, \infty)$

domain: $[-4, \infty)$
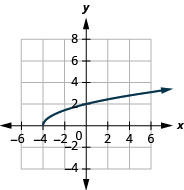
$The figure shows a square root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 4 to 4. The y-axis runs from negative 2 to 6. The function has a starting point at (negative 4, 0) and goes through the points (negative 3, 1) and (0, 2).$
Figure 8.7.9
$[0, \infty)$

domain: $[0, \infty)$
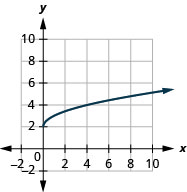
$The figure shows a square root function graph on the x y-coordinate plane. The x-axis of the plane runs from 0 to 8. The y-axis runs from 0 to 8. The function has a starting point at (0, 2) and goes through the points (1, 3) and (4, 4).$
Figure 8.7.10
$[2, \infty)$

domain: $[0, \infty)$
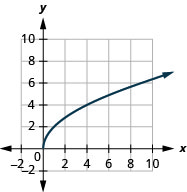
$The figure shows a square root function graph on the x y-coordinate plane. The x-axis of the plane runs from 0 to 8. The y-axis runs from 0 to 8. The function has a starting point at (0, 0) and goes through the points (1, 2) and (4, 4).$
Figure 8.7.11
$[0, \infty)$

domain: $(-\infty, 3]$
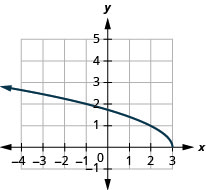
$The figure shows a square root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 6 to 4. The y-axis runs from 0 to 8. The function has a starting point at (3, 0) and goes through the points (2, 1), (negative 1, 2), and (negative 6, 3).$
Figure 8.7.12
$[0, \infty)$

11.

domain: $[0, \infty)$
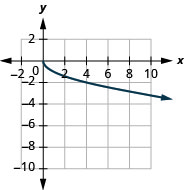
$The figure shows a square root function graph on the x y-coordinate plane. The x-axis of the plane runs from 0 to 8. The y-axis runs from negative 8 to 0. The function has a starting point at (0, 0) and goes through the points (1, negative 1) and (4, negative 2).$
Figure 8.7.13
$(-\infty, 0]$

13.

domain: $(-\infty, \infty)$
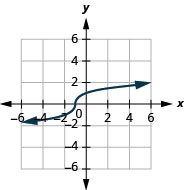
$The figure shows a cube root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 4 to 4. The y-axis runs from negative 4 to 4. The function has a center point at (negative 1, 0) and goes through the points (negative 2, negative 1) and (0, 1).$
Figure 8.7.14
$(-\infty, \infty)$

15.

domain: $(-\infty, \infty)$
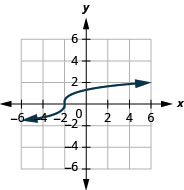
$The figure shows a cube root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 4 to 4. The y-axis runs from negative 4 to 4. The function has a center point at (negative 4, 0) and goes through the points (negative 3, negative 1) and (negative 1, 1).$
Figure 8.7.15
$(-\infty, \infty)$

17.

domain: $(-\infty, \infty)$
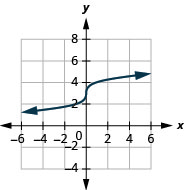
$The figure shows a cube root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 4 to 4. The y-axis runs from negative 2 to 6. The function has a center point at (0, 3) and goes through the points (negative 1, 2) and (1, 4).$
Figure 8.7.16
$(-\infty, \infty)$

19.

domain: $(-\infty, \infty)$
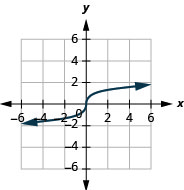
$The figure shows a cube root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 4 to 4. The y-axis runs from negative 4 to 4. The function has a center point at (0, 0) and goes through the points (1, 1) and (negative 1, negative 1).$
Figure 8.7.17
$(-\infty, \infty)$

21.

domain: $(-\infty, \infty)$
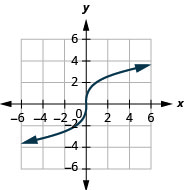
$The figure shows a cube root function graph on the x y-coordinate plane. The x-axis of the plane runs from negative 4 to 4. The y-axis runs from negative 4 to 4. The function has a center point at (0, 0) and goes through the points (1, 2) and (negative 1, negative 2).$
Figure 8.7.18
$(-\infty, \infty)$

Exercise $\PageIndex{20}$ writing exercises

Explain how to find the domain of a fourth root function.
Explain how to find the domain of a fifth root function.
Explain why $y=\sqrt[3]{x}$ is a function.
Explain why the process of finding the domain of a radical function with an even index is different from the process when the index is odd.

Answer

1. Answers may vary

3. Answers may vary

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

The table has 4 columns and 4 rows. The first row is a header row with the headers â€œI canâ€¦â€, â€œConfidentlyâ€, â€œWith some help.â€, and â€œNo â€“ I donâ€™t get it!â€. The first column contains the phrases â€œevaluate a radical functionâ€, â€œfind the domain of a radical functionâ€, and â€œgraph a radical functionâ€. The other columns are left blank so the learner can indicate their level of understanding. — Figure 8.7.19

b. What does this checklist tell you about your mastery of this section? What steps will you take to improve?

Search

Text Color

Text Size

Margin Size

Font Type

Exercise \(\PageIndex{17}\) Evaluate a Radical Function

Exercise \(\PageIndex{18}\) Find the Domain of a Radical Function

Exercise \(\PageIndex{19}\) graph radical functions

Exercise \(\PageIndex{20}\) writing exercises