Skip to main content
Mathematics LibreTexts

10.4E: Exercises

  1. Last updated
  2. Save as PDF
  • Page ID
    30229

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Section 10.3 Exercises

    Practice Makes Perfect

    Exercise \(\PageIndex{21}\) Convert Between Exponential and Logarithmic Form

    In the following exercises, convert from exponential to logarithmic form.

    1. \(4^{2}=16\)
    2. \(2^{5}=32\)
    3. \(3^{3}=27\)
    4. \(5^{3}=125\)
    5. \(10^{3}=1000\)
    6. \(10^{-2}=\frac{1}{100}\)
    7. \(x^{\frac{1}{2}}=\sqrt{3}\)
    8. \(x^{\frac{1}{3}}=\sqrt[3]{6}\)
    9. \(32^{x}=\sqrt[4]{32}\)
    10. \(17^{x}=\sqrt[5]{17}\)
    11. \(\left(\frac{1}{4}\right)^{2}=\frac{1}{16}\)
    12. \(\left(\frac{1}{3}\right)^{4}=\frac{1}{81}\)
    13. \(3^{-2}=\frac{1}{9}\)
    14. \(4^{-3}=\frac{1}{64}\)
    15. \(e^{x}=6\)
    16. \(e^{3}=x\)
    Answer

    2. \(\log _{2} 32=5\)

    4. \(\log _{5} 125=3\)

    6. \(\log \frac{1}{100}=-2\)

    8. \(\log _{x} \sqrt[3]{6}=\frac{1}{3}\)

    10. \(\log _{17} \sqrt[5]{17}=x\)

    12. \(\log _{\frac{1}{3}} \frac{1}{81}=4\)

    14. \(\log _{4} \frac{1}{64}=-3\)

    16. \(\ln x=3\)

    Exercise \(\PageIndex{22}\) Convert Between Exponential and Logarithmic Form

    In the following exercises, convert each logarithmic equation to exponential form.

    1. \(3=\log _{4} 64\)
    2. \(6=\log _{2} 64\)
    3. \(4=\log _{x} 81\)
    4. \(5=\log _{x} 32\)
    5. \(0=\log _{12} 1\)
    6. \(0=\log _{7} 1\)
    7. \(1=\log _{3} 3\)
    8. \(1=\log _{9} 9\)
    9. \(-4=\log _{10} \frac{1}{10,000}\)
    10. \(3=\log _{10} 1,000\)
    11. \(5=\log _{e} x\)
    12. \(x=\log _{e} 43\)
    Answer

    2. \(64=2^{6}\)

    4. \(32=x^{5}\)

    6. \(1=7^{0}\)

    8. \(9=9^{1}\)

    10. \(1,000=10^{3}\)

    12. \(43=e^{x}\)

    Exercise \(\PageIndex{23}\) Evaluate Logarithmic Functions

    In the following exercises, find the value of \(x\) in each logarithmic equation.

    1. \(\log _{x} 49=2\)
    2. \(\log _{x} 121=2\)
    3. \(\log _{x} 27=3\)
    4. \(\log _{x} 64=3\)
    5. \(\log _{3} x=4\)
    6. \(\log _{5} x=3\)
    7. \(\log _{2} x=-6\)
    8. \(\log _{3} x=-5\)
    9. \(\log _{\frac{1}{4}} \frac{1}{16}=x\)
    10. \(\log _{\frac{1}{3}} \frac{1}{9}=x\)
    11. \(\log _{\frac{1}{4}} 64=x\)
    12. \(\log _{\frac{1}{9}} 81=x\)
    Answer

    2. \(x=11\)

    4. \(x=4\)

    6. \(x=125\)

    8. \(x=\frac{1}{243}\)

    10. \(x=2\)

    12. \(x=-2\)

    Exercise \(\PageIndex{24}\) Evaluate Logarithmic Functions

    In the following exercises, find the exact value of each logarithm without using a calculator.

    1. \(\log _{7} 49\)
    2. \(\log _{6} 36\)
    3. \(\log _{4} 1\)
    4. \(\log _{5} 1\)
    5. \(\log _{16} 4\)
    6. \(\log _{27} 3\)
    7. \(\log _{\frac{1}{2}} 2\)
    8. \(\log _{\frac{1}{2}} 4\)
    9. \(\log _{2} \frac{1}{16}\)
    10. \(\log _{3} \frac{1}{27}\)
    11. \(\log _{4} \frac{1}{16}\)
    12. \(\log _{9} \frac{1}{81}\)
    Answer

    2. \(2\)

    4. \(0\)

    6. \(\frac{1}{3}\)

    8. \(-2\)

    10. \(-3\)

    12. \(-2\)

    Exercise \(\PageIndex{25}\) Graph Logarithmic Functions

    In the following exercises, graph each logarithmic function.

    1. \(y=\log _{2} x\)
    2. \(y=\log _{4} x\)
    3. \(y=\log _{6} x\)
    4. \(y=\log _{7} x\)
    5. \(y=\log _{1.5} x\)
    6. \(y=\log _{2.5} x\)
    7. \(y=\log _{\frac{1}{3}} x\)
    8. \(y=\log _{\frac{1}{5}} x\)
    9. \(y=\log _{0.4} x\)
    10. \(y=\log _{0.6} x\)
    Answer

    2.

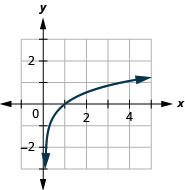
    This figure shows the logarithmic curve going through the points (1 over 4, negative 1), (1, 0), and (4, 1).
    Figure 10.3.19

    4.

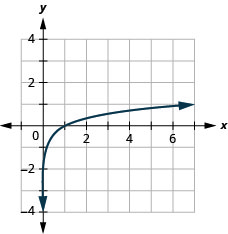
    This figure shows that the logarithmic curve going through the points (1 over 7, negative 1), (1, 0), and (7, 1).
    Figure 10.3.20

    6.

    This figure shows the logarithmic curve going through the points (2 over 5, negative 1), (1, 0), and (2.5, 1).
    Figure 10.3.21

    8.

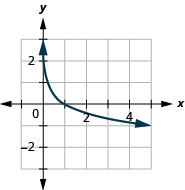
    This figure shows the logarithmic curve going through the points (1 over 5, 1), (1, 0), and (5, negative 1).
    Figure 10.3.22

    10.

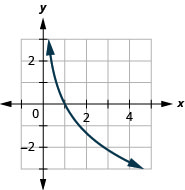
    This figure shows the logarithmic curve going through the points (3 over 5, 1), (1, 0), and (5 over 3, negative 1).
    Figure 10.3.23
    Exercise \(\PageIndex{26}\) Solve Logarithmic Equations

    In the following exercises, solve each logarithmic equation.

    1. \(\log _{a} 16=2\)
    2. \(\log _{a} 81=2\)
    3. \(\log _{a} 8=3\)
    4. \(\log _{a} 27=3\)
    5. \(\log _{a} 32=2\)
    6. \(\log _{a} 24=3\)
    7. \(\ln x=5\)
    8. \(\ln x=4\)
    9. \(\log _{2}(5 x+1)=4\)
    10. \(\log _{2}(6 x+2)=5\)
    11. \(\log _{3}(4 x-3)=2\)
    12. \(\log _{3}(5 x-4)=4\)
    13. \(\log _{4}(5 x+6)=3\)
    14. \(\log _{4}(3 x-2)=2\)
    15. \(\ln e^{4 x}=8\)
    16. \(\ln e^{2 x}=6\)
    17. \(\log x^{2}=2\)
    18. \(\log \left(x^{2}-25\right)=2\)
    19. \(\log _{2}\left(x^{2}-4\right)=5\)
    20. \(\log _{3}\left(x^{2}+2\right)=3\)
    Answer

    2. \(a=9\)

    4. \(a=3\)

    6. \(a=\sqrt[3]{24}\)

    8. \(x=e^{4}\)

    10. \(x=5\)

    12. \(x=17\)

    14. \(x=6\)

    16. \(x=3\)

    18. \(x=-5 \sqrt{5}, x=5 \sqrt{5}\)

    20. \(x=-5, x=5\)

    Exercise \(\PageIndex{27}\) Use Logarithmic Models in Applications

    In the following exercises, use a logarithmic model to solve.

    1. What is the decibel level of normal conversation with intensity \(10^{−6}\) watts per square inch?
    2. What is the decibel level of a whisper with intensity \(10^{−10}\) watts per square inch?
    3. What is the decibel level of the noise from a motorcycle with intensity \(10^{−2}\) watts per square inch?
    4. What is the decibel level of the sound of a garbage disposal with intensity \(10^{−2}\) watts per square inch?
    5. In 2014, Chile experienced an intense earthquake with a magnitude of \(8.2\) on the Richter scale. In 2010, Haiti also experienced an intense earthquake which measured \(7.0\) on the Richter scale. Compare the intensities of the two earthquakes.
    6. The Los Angeles area experiences many earthquakes. In 1994, the Northridge earthquake measured magnitude of \(6.7\) on the Richter scale. In 2014, Los Angeles also experienced an earthquake which measured \(5.1\) on the Richter scale. Compare the intensities of the two earthquakes.
    Answer

    2. A whisper has a decibel level of \(20\) dB.

    4. The sound of a garbage disposal has a decibel level of \(100\) dB.

    6. The intensity of the 1994 Northridge earthquake in the Los Angeles area was about \(40\) times the intensity of the 2014 earthquake.

    Exercise \(\PageIndex{28}\) Writing Exercises
    1. Explain how to change an equation from logarithmic form to exponential form.
    2. Explain the difference between common logarithms and natural logarithms.
    3. Explain why \(\log _{a} a^{x}=x\).
    4. Explain how to find the \(\log _{7} 32\) on your calculator.
    Answer

    2. Answers may vary

    4. Answers may vary

    Self Check

    a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

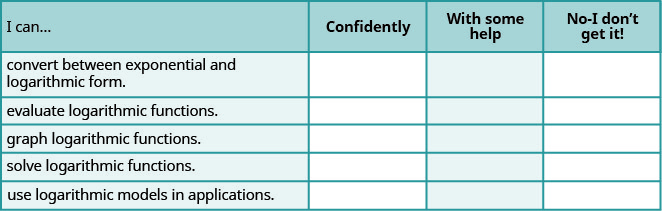
    This table has four rows and five columns. The first row, which serves as a header, reads I can…, Confidently, With some help, and No—I don’t get it. The first column below the header row reads Convert between exponential and logarithmic form, evaluate logarithmic functions, graph logarithmic functions, solve logarithmic equations, and use logarithmic models in applications. The rest of the cells are blank.
    Figure 10.3.24

    b. After reviewing this checklist, what will you do to become confident for all objectives?

    This page titled 10.4E: Exercises is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform.