Skip to main content
Mathematics LibreTexts

11.6E: Exercises

  1. Last updated
  2. Save as PDF
  • Page ID
    30576

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Practice Makes Perfect

    Exercise \(\PageIndex{17}\) Solve a System of Nonlinear Equations Using Graphing

    In the following exercises, solve the system of equations by using graphing.

    1. \(\left\{\begin{array}{l}{y=2 x+2} \\ {y=-x^{2}+2}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{y=6 x-4} \\ {y=2 x^{2}}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x+y=2} \\ {x=y^{2}}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x-y=-2} \\ {x=y^{2}}\end{array}\right.\)
    5. \(\left\{\begin{array}{l}{y=\frac{3}{2} x+3} \\ {y=-x^{2}+2}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{y=x-1} \\ {y=x^{2}+1}\end{array}\right.\)
    7. \(\left\{\begin{array}{l}{x=-2} \\ {x^{2}+y^{2}=4}\end{array}\right.\)
    8. \(\left\{\begin{array}{l}{y=-4} \\ {x^{2}+y^{2}=16}\end{array}\right.\)
    9. \(\left\{\begin{array}{l}{x=2} \\ {(x+2)^{2}+(y+3)^{2}=16}\end{array}\right.\)
    10. \(\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y-4)^{2}=25}\end{array}\right.\)
    11. \(\left\{\begin{array}{l}{y=-2 x+4} \\ {y=\sqrt{x}+1}\end{array}\right.\)
    12. \(\left\{\begin{array}{l}{y=-\frac{1}{2} x+2} \\ {y=\sqrt{x}-2}\end{array}\right.\)
    Answer

    2.

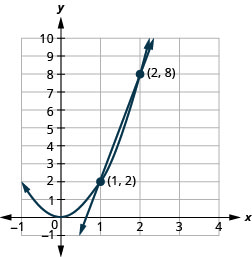
    This graph shows the equations of a system, y is equal to 6 x minus 4 which is a line and y is equal to 2 x squared which is a parabola, on the x y-coordinate plane. The vertex of the parabola is (0, 0) and the parabola opens upward. The line has a slope of 6. The line and parabola intersect at the points (1, 2) and (2, 8), which are labeled. The solutions are (1, 2) and (2, 8).
    Figure 11.5.61

    4.

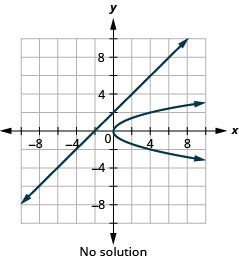
    This graph shows the equations of a system, x minus y is equal to negative 2 which is a line and x is equal to y squared which is a rightward-opening parabola, on the x y-coordinate plane. The vertex of the parabola is (0, 0) and it passes through the points (1, 1) and (1, negative 1). The line has a slope of 1 and a y-intercept at 2. The line and parabola do not intersect, so the system has no solution.
    Figure 11.5.62

    6.

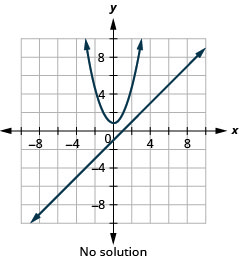
    This graph shows the equations of a system, y is x minus 1 which is a line and y is equal to x squared plus 1 which is an upward-opening parabola, on the x y-coordinate plane. The vertex of the parabola is (0, 1) and it passes through the points (negative 1, 2) and (1, 2). The line has a slope of 1 and a y-intercept at negative 1. The line and parabola do not intersect, so the system has no solution.
    Figure 11.5.63

    8.

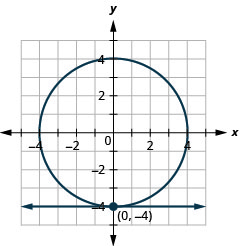
    This graph shows the equations of a system, x is equal to negative 2 which is a line and x squared plus y squared is equal to 16 which is a circle, on the x y-coordinate plane. The line is horizontal. The center of the circle is (0, 0) and the radius of the circle is 4. The line and circle intersect at (negative 2, 0), so the solution of the system is (negative 2, 0).
    Figure 11.5.64

    10.

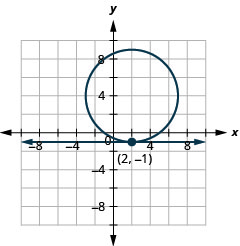
    This graph shows the equations of a system, x is equal to 2 which is a line and the quantity x minus 2 end quantity squared plus the quantity y minus 4 end quantity squared is equal to 25 which is a circle, on the x y-coordinate plane. The line is horizontal. The center of the circle is (2, 4) and the radius of the circle is 5. The line and circle intersect at (2, negative 1), so the solution of the system is (2, negative 1).
    Figure 11.5.65

    12.

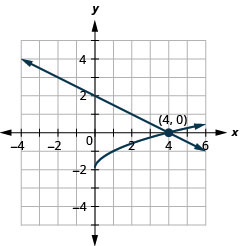
    This graph shows the equations of a system, y is equal to negative one-half x plus 2 which is a line and the y is equal to the square root of x minus 2, on the x y-coordinate plane. The curve for y is equal to the square root of x minus 2 The curve for y is equal to the square root of x plus 1 where x is greater than or equal to 0 and y is greater than or equal to negative 2. The line and square root curve intersect at (4, 0), so the solution is (4, 0).
    Figure 11.5.66
    Exercise \(\PageIndex{18}\) Solve a System of Nonlinear Equations Using Substitution

    In the following exercises, solve the system of equations by using substitution.

    1. \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {y=\frac{1}{2} x-1}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x+3}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=x+3}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {x=2}\end{array}\right.\)
    5. \(\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=4}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
    7. \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
    8. \(\left\{\begin{array}{l}{2 y^{2}-x=0} \\ {y=x+1}\end{array}\right.\)
    9. \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=x+3}\end{array}\right.\)
    10. \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
    11. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {x-y=1}\end{array}\right.\)
    12. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x+y=10}\end{array}\right.\)
    Answer

    2. \((-1,0),(0,3)\)

    4. \((2,0)\)

    6. \((12,-5),(12,5)\)

    8. No solution

    10. \((0,-4),(1,-3)\)

    12. \((3,4),(5,0)\)

    Exercise \(\PageIndex{19}\) Solve a System of Nonlinear Equations Using Elimination

    In the following exercises, solve the system of equations by using elimination.

    1. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y=8}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y=4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}+2 y=1}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=2}\end{array}\right.\)
    5. \(\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=3}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {y^{2}-x=2}\end{array}\right.\)
    7. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {2 x^{2}-3 y^{2}=5}\end{array}\right.\)
    8. \(\left\{\begin{array}{l}{x^{2}+y^{2}=20} \\ {x^{2}-y^{2}=-12}\end{array}\right.\)
    9. \(\left\{\begin{array}{l}{x^{2}+y^{2}=13} \\ {x^{2}-y^{2}=5}\end{array}\right.\)
    10. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
    11. \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
    12. \(\left\{\begin{array}{l}{x^{2}-y^{2}=3} \\ {2 x^{2}+y^{2}=6}\end{array}\right.\)
    13. \(\left\{\begin{array}{l}{4 x^{2}-y^{2}=4} \\ {4 x^{2}+y^{2}=4}\end{array}\right.\)
    14. \(\left\{\begin{array}{l}{x^{2}-y^{2}=-5} \\ {3 x^{2}+2 y^{2}=30}\end{array}\right.\)
    15. \(\left\{\begin{array}{l}{x^{2}-y^{2}=1} \\ {x^{2}-2 y=4}\end{array}\right.\)
    16. \(\left\{\begin{array}{l}{2 x^{2}+y^{2}=11} \\ {x^{2}+3 y^{2}=28}\end{array}\right.\)
    Answer

    2. \((0,-4),(-\sqrt{7}, 3),(\sqrt{7}, 3)\)

    4. \((0,-2),(-\sqrt{3}, 1),(\sqrt{3}, 1)\)

    6. \((-2,0),(1,-\sqrt{3}),(1, \sqrt{3})\)

    8. \((-2,-4),(-2,4),(2,-4),(2,4)\)

    10. \((-4,0),(4,0)\)

    12. \((-\sqrt{3}, 0),(\sqrt{3}, 0)\)

    14. \((-2,-3),(-2,3),(2,-3),(2,3)\)

    16. \((-1,-3),(-1,3),(1,-3),(1,3)\)

    Exercise \(\PageIndex{20}\) Use a System of Nonlinear Equations to Solve Applications

    In the following exercises, solve the problem using a system of equations.

    1. The sum of two numbers is \(−6\) and the product is \(8\). Find the numbers.
    2. The sum of two numbers is \(11\) and the product is \(−42\). Find the numbers.
    3. The sum of the squares of two numbers is \(65\). The difference of the number is \(3\). Find the numbers.
    4. The sum of the squares of two numbers is \(113\). The difference of the number is \(1\). Find the numbers.
    5. The difference of the squares of two numbers is \(15\). The difference of twice the square of the first number and the square of the second number is \(30\). Find the numbers.
    6. The difference of the squares of two numbers is \(20\). The difference of the square of the first number and twice the square of the second number is \(4\). Find the numbers.
    7. The perimeter of a rectangle is \(32\) inches and its area is \(63\) square inches. Find the length and width of the rectangle.
    8. The perimeter of a rectangle is \(52\) cm and its area is \(165\) \(\mathrm{cm}^{2}\). Find the length and width of the rectangle.
    9. Dion purchased a new microwave. The diagonal of the door measures \(17\) inches. The door also has an area of \(120\) square inches. What are the length and width of the microwave door?
    10. Jules purchased a microwave for his kitchen. The diagonal of the front of the microwave measures \(26\) inches. The front also has an area of \(240\) square inches. What are the length and width of the microwave?
    11. Roman found a widescreen TV on sale, but isn’t sure if it will fit his entertainment center. The TV is \(60\)”. The size of a TV is measured on the diagonal of the screen and a widescreen has a length that is larger than the width. The screen also has an area of \(1728\) square inches. His entertainment center has an insert for the TV with a length of \(50\) inches and width of \(40\) inches. What are the length and width of the TV screen and will it fit Roman’s entertainment center?
    12. Donnette found a widescreen TV at a garage sale, but isn’t sure if it will fit her entertainment center. The TV is \(50\)”. The size of a TV is measured on the diagonal of the screen and a widescreen has a length that is larger than the width. The screen also has an area of \(1200\) square inches. Her entertainment center has an insert for the TV with a length of \(38\) inches and width of \(27\) inches. What are the length and width of the TV screen and will it fit Donnette’s entertainment center?
    Answer

    2. \(-3\) and \(14\)

    4. \(-7\) and \(-8\) or \(8\) and \(7\)

    6. \(-6\) and \(-4\) or \(-6\) and \(4\) or \(6\) and \(-4\) or \(6\) and \(4\)

    8. If the length is \(11\) cm, the width is \(15\) cm. If the length is \(15\) cm, the width is \(11\) cm.

    10. If the length is \(10\) inches, the width is \(24\) inches. If the length is \(24\) inches, the width is \(10\) inches.

    12. The length is \(40\) inches and the width is \(30\) inches. The TV will not fit Donnette’s entertainment center.

    Exercise \(\PageIndex{21}\) Writing Exercises
    1. In your own words, explain the advantages and disadvantages of solving a system of equations by graphing.
    2. Explain in your own words how to solve a system of equations using substitution.
    3. Explain in your own words how to solve a system of equations using elimination.
    4. A circle and a parabola can intersect in ways that would result in \(0, 1, 2, 3,\) or \(4\) solutions. Draw a sketch of each of the possibilities.
    Answer

    2. Answers may vary

    4. Answers may vary

    Self Check

    a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

    This table has four columns and five rows. The first row is a header and it labels each column, “I can…”, “Confidently,” “With some help,” and “No-I don’t get it!” In row 2, the I can was solve a system of nonlinear equations using graphing. In row 3, the I can solve a system of nonlinear equations using substitution. In row 4, the I can was solve a system of a nonlinear equations using the elimination. In row 5, the I can was use a system of nonlinear equations to solve applications.
    Figure 11.5.67

    b. After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

    This page titled 11.6E: Exercises is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform.