12.3: Arithmetic Sequences
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Determine if a sequence is arithmetic
- Find the general term (nth term) of an arithmetic sequence
- Find the sum of the first n terms of an arithmetic sequence
Before you get started, take this readiness quiz.
- Evaluate 4n−1 for the integers 1,2,3, and 4.
If you missed this problem, review Example 1.6. - Solve the system of equations: {x+y=73x+4y=23.
If you missed this problem, review Example 4.9. - If f(n)=n2(3n+5), find f(1)+f(20).
If you missed this problem, review Example 3.49.
Determine if a Sequence is Arithmetic
The last section introduced sequences and now we will look at two specific types of sequences that each have special properties. In this section we will look at arithmetic sequences and in the next section, geometric sequences.
An arithmetic sequence is a sequence where the difference between consecutive terms is constant. The difference between consecutive terms in an arithmetic sequence, a_{n}-a_{n-1}, is d, the common difference, for n greater than or equal to two.
An arithmetic sequence is a sequence where the difference between consecutive terms is always the same.
The difference between consecutive terms, a_{n}-a_{n-1}, is d, the common difference, for n greater than or equal to two.
Determine if each sequence is arithmetic. If so, indicate the common difference.
- 5,9,13,17,21,25,…
- 4,9,12,17,20,25,…
- 10,3,−4,−11,−18,−25,…
Solution:
To determine if the sequence is arithmetic, we find the difference of the consecutive terms shown.
a. 5,9,13,1721,25,… Find the difference of the consecutive terms.9−513−917−1321−1725−2144444
The sequence is arithmetic. The common difference is d=4.
b. 4,9,12,1720,25,… Find the difference of the consecutive terms.9−412−917−1220−1725−2023535
The sequence is not arithmetic as all the differences between the consecutive terms are not the same. There is no common difference.
c. 10,3,−4,−11−18,−25,… Find the difference of the consecutive terms.3−10−4−3−11−(−4)−18−(−11)−25−(−18)−7−7−7−7−7
Answer:
The sequence is arithmetic. The common difference is d=−7.
Determine if each sequence is arithmetic. If so, indicate the common difference.
- 9,20,31,42,53,64,…
- 12,6,0,−6,−12,−18,…
- 7,1,10,4,13,7,…
- Answer
-
- The sequence is arithmetic with common difference d=11.
- The sequence is arithmetic with common difference d=−6.
- The sequence is not arithmetic as all the differences between the consecutive terms are not the same.
Determine if each sequence is arithmetic. If so, indicate the common difference.
- −4,4,2,10,8,16,…
- −3,−1,1,3,5,7,…
- 7,2,−3,−8,−13,−18,…
- Answer
-
- The sequence is not arithmetic as all the differences between the consecutive terms are not the same.
- The sequence is arithmetic with common difference d=2.
- The sequence is arithmetic with common difference d=−5.
If we know the first term, a1, and the common difference, d, we can list a finite number of terms of the sequence.
Write the first five terms of the sequence where the first term is 5 and the common difference is d=−6.
Solution:
We start with the first term and add the common difference. Then we add the common difference to that result to get the next term, and so on.
a1a2a3a4a555+(−6)−1+(−6)−7+(−6)−13+(−6)−1−7−13−19
Answer:
The sequence is 5,−1,−7,−13,−19,…
Write the first five terms of the sequence where the first term is 7 and the common difference is d=−4.
- Answer
-
7,3,−1,−5,−9,…
Write the first five terms of the sequence where the first term is 11 and the common difference is d=−8.
- Answer
-
11,3,−5,−13,−21,…
Find the General Term (nth Term) of an Arithmetic Sequence
Just as we found a formula for the general term of a sequence, we can also find a formula for the general term of an arithmetic sequence.
Let’s write the first few terms of a sequence where the first term is a1 and the common difference is d. We will then look for a pattern.
As we look for a pattern we see that each term starts with a1.
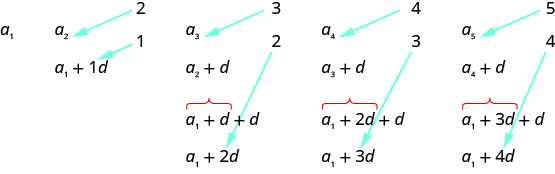
The first term adds 0d to the a1, the second term adds 1d, the third term adds 2d, the fourth term adds 3d, and the fifth term adds 4d. The number of ds that were added to a1 is one less than the number of the term. This leads us to the following
an=a1+(n−1)d
The general term of an arithmetic sequence with first term a1 and the common difference d is
an=a1+(n−1)d
We will use this formula in the next example to find the 15th term of a sequence.
Find the fifteenth term of a sequence where the first term is 3 and the common difference is 6.
Solution:
To find the fifteenth term, a15, use the formula with a1=3andd=6.an=a1+(n−1)dSubstitute in the values.a15=3+(15−1)6Simplify.a15=3+(14)6a15=87
Find the twenty-seventh term of a sequence where the first term is 7 and the common difference is 9.
- Answer
-
241
Find the eighteenth term of a sequence where the first term is 13 and the common difference is −7.
- Answer
-
−106
Sometimes we do not know the first term and we must use other given information to find it before we find the requested term.
Find the twelfth term of a sequence where the seventh term is 10 and the common difference is −2. Give the formula for the general term.
Solution:
To first find the first term, a1, use the formula with a7=10,n=7, and d=−2. Substitute in the values. Simplify.
an=a1+(n−1)d
10=a1+(7−1)(−2)
10=a1+(6)(−2)
10=a1−12
a1=22
Find the twelfth term, a12,using the formula with a1=22, n=12, and d=−2. Substitute in the values. Simplify.
an=a1+(n−1)d
a12=22+(12−1)(−2)
a12=22+(11)(−2)
a12=0
The twelfth term of the sequence is 0,a12=0
To find the general term, substitute the values into the formula.
an=a1+(n−1)d
an=22+(n−1)(−2)
an=22−2n+2
Answer:
The general term is an=−2n+24
Find the eleventh term of a sequence where the ninth term is 8 and the common difference is −3. Give the formula for the general term.
- Answer
-
a11=2. The general term is an=−3n+35
Find the nineteenth term of a sequence where the fifth term is 1 and the common difference is −4.Give the formula for the general term.
- Answer
-
a19=−55. The general term is an=−4n+21
Sometimes the information given leads us to two equations in two unknowns. We then use our methods for solving systems of equations to find the values needed.
Find the first term and common difference of a sequence where the fifth term is 19 and the eleventh term is 37. Give the formula for the general term.
Solution:
Since we know two terms, we can make a system of equations using the formula for the general term.
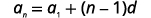 |
|
| We know the value of a5 and a11, so we will use n=5 and n=11. | 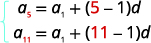 |
Substitute in the values, a5=19 and a11=37. |
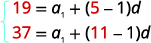 |
| Simplify. | 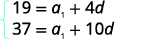 |
| Prepare to eliminate the a1 term by multiplying the top equation by −1. Add the equations. |
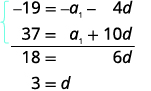 |
| Substituting d=3 back into the first equation. | 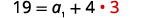 |
| Solve for a1. | 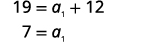 |
| Use the formula with a1=7 and d=3. | 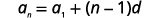 |
| Substitute in the values. | 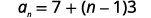 |
| Simplify. | 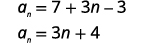 |
| The first term is a1=7. The common difference is d=3. |
|
| The general term of the sequence is an=3n+4. |
Answer:
The general term of the sequence is an=3n+4.
Find the first term and common difference of a sequence where the fourth term is 17 and the thirteenth term is 53. Give the formula for the general term.
- Answer
-
a1=5,d=4. The general term is an=4n+1.
Find the first term and common difference of a sequence where the third term is 2 and the twelfth term is −25. Give the formula for the general term.
- Answer
-
a1=8,d=−3. The general term is an=−3n+11.
Find the Sum of the First n Terms of an Arithmetic Sequence
As with the general sequences, it is often useful to find the sum of an arithmetic sequence. The sum, Sn, of the first n terms of any arithmetic sequence is written as Sn=a1+a2+a3+…+an. To find the sum by merely adding all the terms can be tedious. So we can also develop a formula to find the sum of a sequence using the first and last term of the sequence.
We can develop this new formula by first writing the sum by starting with the first term, a1, and keep adding a d to get the next term as:
Sn=a1+(a1+d)+(a1+2d)+…+an.
We can also reverse the order of the terms and write the sum by starting with an and keep subtracting d to get the next term as
Sn=an+(an−d)+(an−2d)+…+a1.
If we add these two expressions for the sum of the first n terms of an arithmetic sequence, we can derive a formula for the sum of the first n terms of any arithmetic series.
Sn=a1+(a1+d)+(a1+2d)+…+an+Sn=an+(an−d)+(an−2d)+…+a12Sn=(a1+an)+(a1+an)+(a1+an)+⋯+(a1+an)
Because there are n sums of (a1+an) on the right side of the equation, we rewrite the right side as n(a1+an).
2Sn=n(a1+an)
We divide by two to solve for Sn.
Sn=n2(a1+an)
This give us a general formula for the sum of the first n terms of an arithmetic sequence.
The sum, Sn, of the first n terms of an arithmetic sequence is
Sn=n2(a1+an)
where a1 is the first term and an is the nth term.
We apply this formula in the next example where the first few terms of the sequence are given.
Find the sum of the first 30 terms of the arithmetic sequence: 8,13,18,23,28,…
Solution:
To find the sum, we will use the formula Sn=n2(a1+an). We know a1=8,d=5 and n=30, but we need to find an in order to use the sum formula.
Find an where a1=8,d=5 and n=30. Simplify.
an=a1+(n−1)da30=8+(30−1)5a30=8+(29)5a30=153
Knowing a1=8,n=30, and a30=153, use the sum formula. Substitute in the values. Simplify. Simplify.
Sn=n2(a1+an)S30=302(8+153)S30=15(161)S30=2,415
Find the sum of the first 30 terms of the arithmetic sequence: 5,9,13,17,21,…
- Answer
-
1,890
Find the sum of the first 30 terms of the arithmetic sequence: 7,10,13,16,19,…
- Answer
-
1,515
In the next example, we are given the general term for the sequence and are asked to find the sum of the first 50 terms.
Find the sum of the first 50 terms of the arithmetic sequence whose general term is an=3n−4.
Solution:
To find the sum, we will use the formula Sn=n2(a1+an). We know n=50, but we need to find a1 and an in order to use the sum formula.
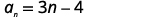 |
|
| Find a1, by substituting n=1. | 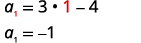 |
| Find an by substituting n=50. | 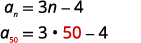 |
| Simplify. | 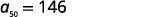 |
| Knowing n=50,a1=−1, and a50=146 use the sum formula. | 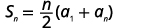 |
| Substitute in the values. | 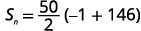 |
| Simplify. | 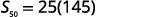 |
| Simplify. | 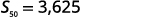 |
Find the sum of the first 50 terms of the arithmetic sequence whose general term is an=2n−5.
- Answer
-
2,300
Find the sum of the first 50 terms of the arithmetic sequence whose general term is an=4n+3.
- Answer
-
5,250
In the next example we are given the sum in summation notation. To add all the terms would be tedious, so we extract the information needed to use the formula to find the sum of the first n terms.
Find the sum: ∑25i=1(4i+7).
Solution:
To find the sum, we will use the formula Sn=n2(a1+an). We know n=25, but we need to find a1 and an in order to use the sum formula.
| Expand the summation notation. |
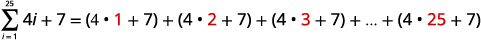
|
| Simplify. |
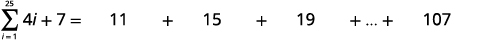
|
| Identify a1. |  |
| Identify a25. |

|
| Knowing n=25,a1=11, and a25=107 use the sum formula. |  |
| Substitute in the values. |  |
| Simplify. |  |
| Simplify. |  |
Find the sum: ∑30i=1(6i−4).
- Answer
-
2,670
Find the sum: ∑35i=1(5i−3).
- Answer
-
3,045
Access these online resources for additional instruction and practice with arithmetic sequences
Key Concepts
- General Term (nth term) of an Arithmetic Sequence
The general term of an arithmetic sequence with first term a1 and the common difference d isan=a1+(n−1)d
- Sum of the First n Terms of an Arithmetic Sequence
The sum, Sn, of the first \n terms of an arithmetic sequence, where a1 is the first term and an is the nth term isSn=n2(a1+an)
Glossary
- arithmetic sequence
- An arithmetic sequence is a sequence where the difference between consecutive terms is constant.
- common difference
- The difference between consecutive terms in an arithmetic sequence, an−an−1, is d, the common difference, for n greater than or equal to two.


