2.3: Parallel and perpendicular lines
- Page ID
- 45035
In this section, we discuss parallel and perpendicular lines. The relationship between parallel lines and between perpendicular lines is unique, where the slope will be most interesting to us in this section.
The Slope of Parallel and Perpendicular Lines
Find the slope of each line and compare. What is interesting about the slopes?
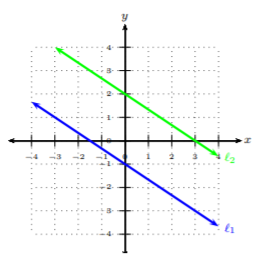
Solution
Looking at \(ℓ_1\), we can start at \((−3, 1)\) and reach the next point at \((0, −1)\). We see that we will move down two units and run to the right \(3\) units. Hence, \(ℓ_1\)’s slope is \(−\frac{2}{3}\). Now let’s look at \(ℓ_2\) and obtain its slope. We will start at \((0, 2)\) and reach the next point at \((3, 0)\). We see that we will move down two units and run to the right \(3\) units. Hence, \(ℓ_2\)’s slope is \(−\frac{2}{3}\). The slopes of \(ℓ_1\) and \(ℓ_2\) are \(−\frac{2}{3}\); they have the same exact slope but different \(y\)-intercepts.
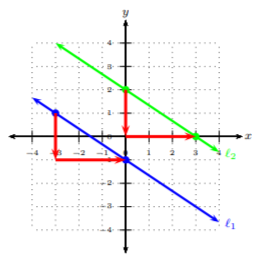
Let \(m_1\) and \(m_2\) be slopes for lines \(ℓ_1\) and \(ℓ_2\), respectively. Lines \(ℓ_1\) and \(ℓ_2\) are parallel to each other if they have the same slope, but different \(y\)-intercepts, i.e., \(m_1 = m_2\).
Find the slope of each line and compare. What is interesting about the slopes?
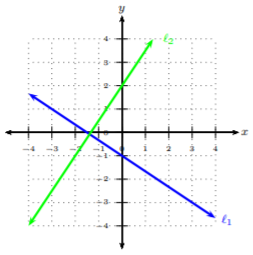
Solution
Looking at \(ℓ_1\), we can start at \((−3, 1)\) and reach the next point at \((0, −1)\). We see that we will move down two units and run to the right \(3\) units. Hence, \(ℓ_1\)’s slope is \(−\frac{2}{3}\). Now let’s look at \(ℓ_2\) and obtain its slope. We will start at \((−2, −1)\) and reach the next point at \((0, 2)\). We see that we will move up three units and run to the right \(2\) units. Hence, \(ℓ_2\)’s slope is \(\frac{3}{2}\). The slopes of \(ℓ_1\) and \(ℓ_2\) are negative reciprocals, i.e., if one has slope \(m\), then a line perpendicular to it will have slope \(−\frac{1}{m}\). Also, note that if two lines are perpendicular, they create a right angle at the intersection.
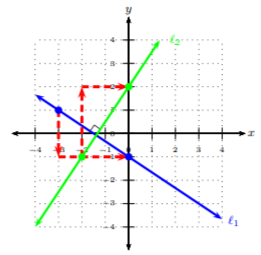
Let \(m_1\) and \(m_2\) be slopes for lines \(ℓ_1\) and \(ℓ_2\), respectively. Lines \(ℓ_1\) and \(ℓ_2\) are perpendicular to each other if they have negative reciprocal slopes, i.e., \(ℓ_1\) has slope \(m_1\) and \(ℓ_2\) has slope \(m_2 = −\frac{1}{m_1}\).
Find the slope of a line parallel to \(5y − 2x = 7\).
Solution
We need to rewrite the equation in slope-intercept form. Then we can identify the slope and the slope for a line parallel to it.
\[\begin{array}{rl}5y-2x=7&\text{Isolate the variable term }5y \\ 5y-2x+\color{blue}{2x}\color{black}{}=7+\color{blue}{2x}\color{black}{}&\text{Simplify} \\ 5y=2x+7&\text{Multiply by the reciprocal of }5 \\ \color{blue}{\frac{1}{5}}\color{black}{}\cdot 5y=\color{blue}{\frac{1}{5}}\color{black}{}\cdot 2x+7\cdot\color{blue}{\frac{1}{5}}\color{black}{}&\text{Simplify} \\ y=\frac{2}{5}x+\frac{7}{5}\end{array}\nonumber\]
We see the slope of the given line is \(\frac{2}{5}\). By the definition, a line parallel will have the same slope \(\frac{2}{5}\).
Find the slope of a line perpendicular to \(3x − 4y = 2\).
Solution
We need to rewrite the equation in slope-intercept form. Then we can identify the slope and the slope for a line perpendicular to it.
\[\begin{array}{rl}3x-4y=2&\text{Isolate the variable term }-4y \\ 3x-4y+\color{blue}{(-3x)}\color{black}{}=2+\color{blue}{(-3x)}\color{black}{}&\text{Simplify} \\ -4y=-3x+2&\text{Multiply by the reciprocal of }-4 \\ \color{blue}{-\frac{1}{4}}\color{black}{}\cdot -4y=\color{blue}{-\frac{1}{4}}\color{black}{}\cdot -3x+2\cdot\color{blue}{-\frac{1}{4}}\color{black}{}&\text{Simplify} \\ y=\frac{3}{4}x-\frac{1}{2}\end{array}\nonumber\]
We see the slope of the given line is \(\frac{3}{4}\). By the definition, a line perpendicular will have a negative reciprocal slope \(-\frac{4}{3}\).
Obtain Equations for Parallel and Perpendicular Lines
Once we have obtained the slope for a line perpendicular or parallel, it is possible to find the complete equation of the second line if we are given a point on the second line.
Find the equation of a line passing through \((4, −5)\) and parallel to \(2x − 3y = 6\).
Solution
First, we can rewrite the given line in slope-intercept form to obtain the slope for a line parallel to it: \[\begin{array}{rl}2x-3y=6&\text{Isolate the variable term }-3y \\ 2x-3y+\color{blue}{(-2x)}\color{black}{}=6+\color{blue}{(-2x)}\color{black}{}&\text{Simplify} \\ -3y=-2x+6&\text{Multiply by the reciprocal of }-3 \\ \color{blue}{-\frac{1}{3}}\color{black}{}\cdot -3y=\color{blue}{-\frac{1}{3}}\color{black}{}\cdot -2x+6\cdot\color{blue}{-\frac{1}{3}}\color{black}{}&\text{Simplify} \\ y=\frac{2}{3}x-2\end{array}\nonumber\]
We see the slope of the given line is \(\frac{2}{3}\). By the definition, a line parallel will have the same slope \(\frac{2}{3}\). Next, we can use the point-slope formula to obtain the equation of the line passing through \((4, −5)\) with slope \(\frac{2}{3}\): \[\begin{array}{rl}y-y_1=m(x-x_1)&\text{Substitute in the point and slope} \\ y-(-5)=\frac{2}{3}(x-4)&\text{Simplify signs} \\ y+5=\frac{2}{3}(x-4)&\text{A line parallel to }2x-3y=6\text{ in point-slope form}\end{array}\nonumber\]
Find the equation of the line, in slope-intercept form, passing through \((6, −9)\) and perpendicular to \(y = −\frac{3}{5}x + 4\).
Solution
Since the given line is in slope-intercept form, we can easily observe the slope and the slope for a line perpendicular. We see the slope of the given line is \(−\frac{3}{5}\). By the definition, a line perpendicular will have a negative reciprocal slope \(\frac{5}{3}\). Next, we can use the point-slope formula to obtain the equation, in slope-intercept form, of the line passing through \((6, −9)\) with slope \(\frac{5}{3}\): \[\begin{array}{rl} y-y_1=m(x-x_1)&\text{Substitute in the point and slope} \\ y-(-9)=\frac{5}{3}(x-6)&\text{Simplify signs} \\ y+9=\frac{5}{3}(x-6)&\text{Distribute} \\ y+9=\frac{5}{3}x-10&\text{Isolate the variable term }y \\ y+9+\color{blue}{(-9)}\color{black}{}=\frac{5}{3}x-10+\color{blue}{(-9)}\color{black}{}&\text{Simplify} \\ y=\frac{5}{3}x-19&\text{A line perpendicular to }y=-\frac{3}{5}x+4\text{ in slope-intercept form}\end{array}\nonumber\]
Lines with zero slopes and undefined slopes may seem like opposites because a horizontal line has slope zero and a vertical line has slope that is undefined. Since a horizontal line is perpendicular to a vertical line, we can say, by definition, the slopes are negative reciprocals, i.e., \(m_1 = 0\) would imply \(m_2 = −\frac{1}{0}\), which is undefined.
Find the equation of the line passing through \((3, 4)\) and perpendicular to \(x = −2\).
Solution
Since \(x = −2\) is a vertical line, then this line has slope that is undefined. Hence, a line perpendicular to it will have slope zero, i.e., \(m = 0\). Next, we can use the point-slope formula to obtain the equation, in slope-intercept form, of the line passing through \((3, 4)\) with slope \(m = 0\): \[\begin{array}{rl}y-y_1=m(x-x_1)&\text{Substitute in the point and slope} \\ y-4=0(x-3)&\text{Distribute} \\ y-4=0&\text{Isolate the variable term }y \\ y-4+\color{blue}{4}\color{black}{}=0+\color{blue}{4}\color{black}{}&\text{Simplify} \\ y=4&\text{A line perpendicular to }x=-2\end{array}\nonumber\]
Now, since we are aware that a line perpendicular to a vertical line is a horizontal line and we were given a point \((3, 4)\), we could have easily jumped to the equation, \(y = 4\).
Parallel and Perpendicular Lines Homework
Given the line, find the slope of a line parallel.
\(y = 2x + 4\)
\(y = 4x − 5\)
\(x − y = 4\)
\(7x + y = −2\)
\(y = − \frac{2}{3} x + 5\)
\(y = − \frac{10}{3} x − 5\)
\(6x − 5y = 20\)
\(3x + 4y = −8\)
Given the line, find the slope of a line perpendicular.
\(x=3\)
\(y = −\frac{1}{3} x\)
\(x − 3y = −6\)
\(x + 2y = 8\)
\(y = − \frac{1}{2} x − 1\)
\(y = \frac{4}{5} x\)
\(3x − y = −3\)
\(8x − 3y = −9\)
Find the equation of the line, in point-slope form, passing through the point and given the line to be parallel or perpendicular.
\((2, 5)\); parallel to \(x = 0\)
\((5, 2)\); parallel to \(y = \frac{7}{5} x + 4\)
\((3, 4)\); parallel to \(y = \frac{9}{2} x − 5\)
\((1, −1)\); parallel to \(y = − \frac{3}{4} x + 3\)
\((2, 3)\); parallel to \(y = \frac{7}{5}x + 4\)
\((−1, 3)\); parallel to \(y = −3x − 1\)
\((4, 2)\); parallel to \(x = 0\)
\((1, 4)\); parallel to \(y = \frac{7}{5} x + 2\)
\((1, −5)\); perpendicular to \(−x + y = 1\)
\((1, −2)\); perpendicular to \(−x + 2y = 2\)
\((5, 2)\); perpendicular to \(5x + y = −3\)
\((1, 3)\); perpendicular to \(−x + y = 1\)
\((4, 2)\); perpendicular to \(−4x + y = 0\)
\((−3, −5)\); perpendicular to \(3x + 7y = 0\)
\((2, −2)\); perpendicular to \(3y − x = 0\)
\((−2, 5)\); perpendicular to \(y − 2x = 0\)
Find the equation of the line, in slope-intercept form, passing through the point and given the line to be parallel or perpendicular.
\((4, −3)\); parallel to \(y = −2x\)
\((−5, 2)\); parallel to \(y = \frac{3}{5} x\)
\((−3, 1)\); parallel to \(y = − \frac{4}{3} x − 1\)
\((−4, 0)\); parallel to \(y = − \frac{5}{4} x + 4\)
\((−4, −1)\); parallel to \(y = − \frac{1}{2}x + 1\)
\((2, 3)\); parallel to \(y = \frac{5}{2} x − 1\)
\((−2, −1)\); parallel to \(y = − \frac{1}{2} x − 2\)
\((−5, −4)\); parallel to \(y = \frac{3}{5} x − 2\)
\((4, 3)\); perpendicular to \(x + y = −1\)
\((−3, −5)\); perpendicular to \(x + 2y = −4\)
\((5, 2)\); perpendicular to \(x = 0\)
\((5, −1)\); perpendicular to \(−5x + 2y = 10\)
\((−2, 5)\); perpendicular to \(−x + y = −2\)
\((2, −3)\); perpendicular to \(−2x + 5y = −10\)
\((4, −3)\); perpendicular to \(−x + 2y = −6\)
\((−4, 1)\); perpendicular to \(4x + 3y = −9\)