3.3: Absolute Value Inequalities
- Page ID
- 45040
When an inequality contains absolute value, we need to rewrite the inequality without the absolute value in order to solve the inequality. Let’s consider \(|x| < 2\). Recall, absolute value is defined as the distance from zero. The idea behind solving \(|x| < 2\) is to find all numbers that have a distance from zero that is less than \(2\). Let’s take a look at this graphically.
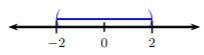
This graph should remind us of tripartite (and) compound inequalities and it is! Now let’s consider \(|x| > 2\). The idea behind solving \(|x| > 2\) is to find all numbers that have a distance from zero that is more than \(2\). Let’s take a look at this graphically.
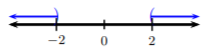
This graph should remind us of or compound inequalities and it is! Absolute inequalities will remind us of the concepts from compound inequalities.
Given below are the cases for absolute value for inequalities in one variable, where \(a\) is a real number.
Case 1. If \(|x| < a\), then \(−a < x < a\).
Case 2. If \(|x| > a\), then \(x < −a\) or \(x > a\). Similar cases for \(≤\) and \(≥\), respectively.
The phrase “absolute value” comes from German mathematician Karl Weierstrass in 1876, though he used the absolute value symbol for complex numbers. The first known use of the symbol for integers comes from a 1939 edition of a college algebra textbook.
Solve the absolute value inequality. Graph the solution and write the solution in interval notation.
\[|4x-5|\geq 6\nonumber\]
Solution
We begin the solution by rewriting the absolute value inequality using the cases in the definition.
\[\begin{array}{rl} |4x-5|\geq 6&\text{Case 2. Rewrite as two inequalities using or} \\ 4x-5\geq 6\quad\text{or}\quad 4x-5\leq -6 &\text{Solve each inequality} \\ 4x\geq 11\quad\text{or}\quad 4x\leq -1&\text{Divide by the coefficient of }x \\ x\geq\frac{11}{4}\quad\text{or}\quad x\leq -\frac{1}{4}&\text{Solution in inequality notation}\end{array}\nonumber\]
Let’s graph each of these inequalities to determine the union of the two sets.
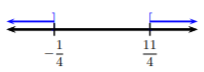
Looking for the union of these two sets, we see the solution is all the numbers to the left of \(−\frac{1}{4}\) (inclusive), or to the right of \(\frac{11}{4}\) (inclusive), or in both. Hence, in interval notation, the solution is \[\left(-\infty ,-\frac{1}{4}\right]\cup\left[\frac{11}{4},\infty\right)\nonumber\]
Isolate the Absolute Value
Recall. In the previous chapter, when solving absolute value equations, we were required to isolate the absolute value term before applying the definition. In this section, we will do the same method because methods never change, only problems.
Solve the absolute value inequality. Graph the solution and write the solution in interval notation.
\[-4-3|x|\leq -16\nonumber\]
Solution
We begin the solution by rewriting the absolute value inequality where the absolute value term is isolated on the left side. Then we can apply the cases in the definition.
\[\begin{array}{rl}-4-3|x|\leq -16&\text{Isolate the absolute value term} \\ -3|x|\leq -12&\text{Divide both sides by }-3 \\ |x|\color{blue}{\geq}\color{black}{}4&\text{Case 2. Rewrite as two inequalities using or} \\ x\geq 4\quad\text{or}\quad x\leq -4&\text{Solution in inequality notation}\end{array}\nonumber\]
Let’s graph each of these inequalities to determine the union of the two sets.

Looking for the union of these two sets, we see the solution is all the numbers to the left of \(−4\) (inclusive), or to the right of \(4\) (inclusive), or in both. Hence, in interval notation, the solution is \[(-\infty , -4)\cup [4,\infty )\nonumber\]
Solve the absolute value inequality. Graph the solution and write the solution in interval notation.
\[9-2|4x+1|>3\nonumber\]
Solution
We begin the solution by rewriting the absolute value inequality where the absolute value term is isolated on the left side. Then we can apply the cases in the definition.
\[\begin{array}{rl}9-2|4x+1|>3&\text{Isolate the absolute value term} \\ -2|4x+1|>-6&\text{Divide both sides by }-2 \\ |4x+1|\color{blue}{<}\color{black}{}3&\text{Case 1. Rewrite as a tripartite inequality} \\ -3<4x+1<3&\text{Solve, start by subtracting 1 from all three parts} \\ -4<4x<2&\text{Divide by the coefficient of }x \\ -1<x<\frac{1}{2}&\text{Solution in inequality notation}\end{array}\nonumber\]
Let’s graph this inequality to determine the intersection of the two sets.
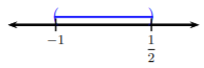
We can see the intersection is all the numbers in between \(−1\) and \(\frac{1}{2}\). Hence, in interval notation, the solution is \(\left(-1,\frac{1}{2}\right)\).
Special Cases with Absolute Value Inequalities
There are special cases with the absolute value inequalities when obtaining a solution. We recall that after evaluating the absolute value of an expression, the result is positive. Hence, if we were to isolate the absolute value on the left side of the inequality, then that result is always positive, i.e., \(|x|\geq 0\), no matter the case.
Solve the absolute value inequality. Graph the solution and write the solution in interval notation.
\[12+4|6x-1|<4\nonumber\]
Solution
We begin the solution by rewriting the absolute value inequality where the absolute value term is isolated on the left side. Then we can apply the cases in the definition.
\[\begin{array}{rl}12+4|6x-1|<4&\text{Isolate the absolute value term} \\ 4|6x-1|<-8&\text{Divide by the coefficient }4 \\ |6x-1|<-2&\text{STOP The absolute value is always non-negative}\end{array}\nonumber\]
By definition of absolute value, \(|6x − 1| ≥ 0\). Hence, \(|6x − 1|\) could never be less than zero, let alone less than \(−2\). Thus, this inequality has no solution or \(∅\). To graph a \(∅\) solution, we leave a number line empty:
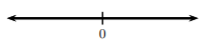
Let’s say, in Example \(\PageIndex{4}\) we didn’t recognize that \(|6x − 1|\) was less than a negative number and we solved as usual. After applying Case 1. in the definition, we would obtain a false statement. In Example \(\PageIndex{4}\), we would have obtained \[2 < 6x − 1 < −2,\nonumber\] but \(2\) isn’t less than \(−2 (2\cancel{<} −2)\). Hence, a false statement. At this point, we would see that the inequality \(|6x − 1| < −2\) has no solution.
Solve the absolute value inequality. Graph the solution and write the solution in interval notation.
\[5-6|x+7|\leq 17\nonumber\]
Solution
We begin the solution by rewriting the absolute value inequality where the absolute value term is isolated on the left side. Then we can apply the cases in the definition.
\[\begin{array}{rl} 5-6|x+7|\leq 17&\text{Isolate the absolute value term} \\ -6|x+7|\leq 12&\text{Divide by the coefficient }-6 \\ |x+7|\color{blue}{\geq}\color{black}{}-2&\text{STOP The absolute value is always non-negative}\end{array}\nonumber\]
By definition of absolute value, \(|x + 7| ≥ 0\). Hence, \(|x + 7|\) is always greater than \(−2\). Thus, this inequality has every real number as a solution and the solution is all real numbers or \((−∞, ∞)\). To graph a \((−∞, ∞)\) solution, we draw a line including the entire number line:
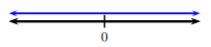
Let’s say, in Example \(\PageIndex{5}\) we didn’t recognize that \(|x + 7|\) was always greater than a negative number and we solved as usual. After applying Case 2. in the definition, we would obtain the same result. In Example \(\PageIndex{5}\), we would have obtained \[x+7\geq -2\quad\text{or}\quad x+7\leq 2,\nonumber\] which results in, after solving, \[x\geq -9\quad\text{or}\quad x\leq -5\nonumber\]
Graphing each inequality, we get
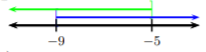
Hence, the solution is \((-\infty ,\infty )\).
Absolute Value Inequalities Homework
Solve the absolute value inequalities. Graph the solution and write the solution in interval notation.
\(|x| < 3\)
\(|2x| < 6\)
\(|x − 2| < 6\)
\(|x − 7| < 3\)
\(|3x − 2| < 9\)
\(1 + 2|x − 1| ≤ 9\)
\(6 − |2x − 5| ≥ 3\)
\(|3x| > 5\)
\(|x − 3| ≥ 3\)
\(|3x − 5| > 3\)
\(4 + 3|x − 1| ≥ 10\)
\(3 − 2|x − 5| ≤ −15\)
\(−2 − 3|4 − 2x| ≥ −8\)
\(4 − 5| − 2x − 7| < −1\)
\(3 − 2|4x − 5| ≥ 1\)
\(−5 − 2|3x − 6| < −8\)
\(4 − 4| − 2x + 6| > −4\)
\(| − 10 + x| ≥ 8\)
\(|x| ≤ 8\)
\(|x + 3| < 4\)
\(|x − 8| < 12\)
\(|x + 3| ≤ 4\)
\(|2x + 5| < 9\)
\(10 − 3|x − 2| ≥ 4\)
\(|x| > 5\)
\(|x − 4| > 5\)
\(|2x − 4| > 6\)
\(3 − |2 − x| < 1\)
\(3 − 2|3x − 1| ≥ −7\)
\(4 − 6| − 6 − 3x| ≤ −5\)
\(−3 − 2|4x − 5| ≥ 1\)
\(−2 + 3|5 − x| ≤ 4\)
\(−2 − 3| − 3x − 5 ≥ −5\)
\(6 − 3|1 − 4x| < −3\)
\(−3 − 4| − 2x − 5| ≥ −7\)


