4.6: Systems of two linear inequalities in two variables
- Page ID
- 45049
In a previous section, we discussed linear inequalities in two variables, where we have the boundary line, dashed or solid, and shading either above or below the \(y\)-intercept, depending on the inequality symbol. For example, let’s recall \(y > x + 4\) and its graph.
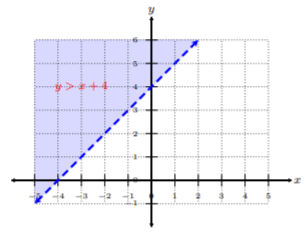
Well, let’s use this same idea for finding the solution to a system of two linear inequalities in two variables. The process is similar, except for the fact that the solution, in this case, is the region with overlap shading. We can present the solution as a shaded region.
A system of two linear inequalities in two variables is a system of the form \[\left\{\begin{array}{ll}ax+by &<c \\ dx+ey &f\end{array}\right.\nonumber\] where \(a,\: b,\: c,\: d,\: e,\) and \(f\) are coefficients, \(x\) and \(y\) are variables, and the form is the same for any combination of \(>,\: ≤,\: ≥\). This system is represented in standard form.
Verifying Solutions
Determine whether the ordered-pairs are a solution to the system: \[\left\{\begin{array}{l}x+4y\geq 10 \\ 3x-2y <12 \end{array}\right.\nonumber\]
- \((-2,4)\)
- \((3,1)\)
Solution
We substitute the ordered pairs into the inequalities and determine if the results are true for both inequalities.
- Let's substitute \((-2,4)\) into the inequalities and determine if the ordered-pair is a solution to both inequalities.
\[\begin{array}{rl} x+4y\stackrel{?}{\geq} 10&\text{Substitute }x=-2\text{ and }y=4 \\ -2+4\color{blue}{(4)}\color{black}{}\stackrel{?}{\geq}10&\text{Simplify} \\ 14\geq 10&\checkmark\text{ True}\end{array}\nonumber\]
\[\begin{array}{rl}3x-2y\stackrel{?}{<}12 &\text{Substitute }x=-2\text{ and }y=4 \\ 3\color{blue}{(-2)}\color{black}{}-2\color{blue}{(4)}\color{black}{}\stackrel{?}{<}&\text{Simplify} \\ -14<12&\checkmark\text{ True}\end{array}\nonumber\]
Hence, \((-2,4)\) is a solution to the system. - Let’s substitute \((3, 1)\) into the inequality and determine if the ordered-pair is a solution to both inequalities.
\[\begin{array}{rl}x+4y\stackrel{?}{\geq}10&\text{Substitute }x=3\text{ and }y=1 \\ 3+4\color{blue}{(1)}\color{black}{}\stackrel{?}{\geq}10&\text{Simplify} \\ 7\cancel{\geq}10& X\text{ False}\end{array}\nonumber\] Hence, \((3, 1)\) is not a solution to the system since \((3, 1)\) is not a solution to the first inequality \(x + 4y ≥ 10\).
Solving a System of Two Linear Inequalities in Two Variables by Graphing
In this section, we solve a system of of two linear inequalities in two variables by graphing. As we can see in the steps given, the process is similar to when we graphed linear inequalities in two variables.
We have to ask, “What is a solution to a system of two linear inequalities in two variables?” Recall, in previous sections of this chapter, we said the solution to a consistent system that is independent was a point of intersection. The intersection point still plays a role with these systems, but we are not looking for one point. We need all points in a shaded common area that make both inequalities in the system true. The intersection point is the corner for this common shaded region.
Given a system of two linear inequalities in two variables, \[\left\{\begin{array}{ll} ax+by &<c \\ dx+ey &<f\end{array}\right. ,\nonumber\] we use the steps below to graph the system, where the same process is applied for any combination of \(>,\: ≤,\: ≥\).
Step 1. Rewrite the inequalities in slope-intercept form, i.e., \(y = mx + b\).
Step 2. Graph the boundary lines according to the two cases:
Case 1. If the inequality is \(<\) or \(>\), then the boundary line is dashed.
Case 2. If the inequality is \(≥\) or \(≤\), then the boundary line is solid.
Step 3. Shade the appropriate regions for each linear inequality.
Step 4. The solution is the region where the shading overlaps.
Step 5. Verify the solution by taking a test point where the shading overlaps that is not on the boundary lines. Ask: Does this ordered pair make both inequalities true?
Solve the system by graphing: \[\left\{\begin{array}{l}3x-2y\leq 6 \\ y>-\frac{1}{4}x+5\end{array}\right.\nonumber\]
Solution
Let’s follow the steps given above to graph the system of linear inequalities in two variables.
Step 1. Rewrite the inequalities in slope-intercept form, i.e., \(y = mx + b\). \[\begin{aligned} 3x-2y&\leq 6 \\ -2y&\leq -3x+6 \\ y&\leq \frac{3}{2}x-3\end{aligned}\] The second inequality is already in slope-intercept form, i.e., \(y > −\frac{1}{4}x + 5\).
Step 2. Graph the boundary lines according to the two cases. Since we have \(≥\) and \(>\), then we have both cases where we have a solid line with \(≥\) and a dashed line with \(>\).
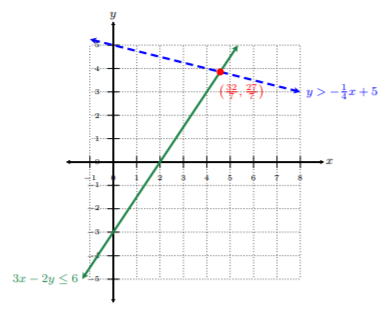
Step 3. Shade the appropriate regions for each linear inequality.
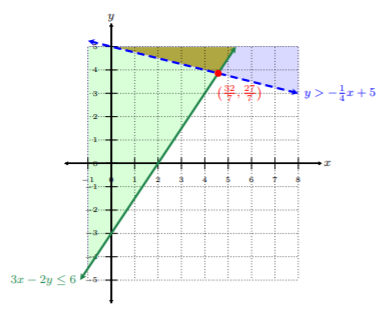
Step 4. The solution is the region where the shading overlaps.
The region where the shading overlaps is the darkened region in the figure above (or olive green). Notice the point of intersection at \(\left(\frac{32}{7},\frac{27}{7}\right)\). The point of intersection is still critical in finding the solution to these types of systems.
Step 5. Verify the solution by taking a test point where the shading overlaps that is not on the boundary lines. Let’s pick the test point \(\color{blue}{(4, 5)}\) as it is a great choice! \[\begin{aligned}3x-2y&\stackrel{?}{\leq}6 \\ 3\color{blue}{(4)}\color{black}{}-2\color{blue}{(5)}\color{black}{}&\stackrel{?}{\leq}6 \\ 2&\leq 6\quad\checkmark\text{True}\end{aligned}\]
\[\begin{aligned} y&\stackrel{?}{>}-\frac{1}{4}x+5 \\ \color{blue}{5}\color{black}{}&\stackrel{?}{>}-\frac{1}{4}\color{blue}{(4)}\color{black}{}+5 \\ 5&>4\quad\checkmark\text{ True}\end{aligned}\] Hence, \((4,5)\) makes both inequalities true.
Thus, the darkened region (or olive green) is the solution.
Systems of Two Linear Inequalities in Two Variables Homework
Determine whether the given ordered pairs are solutions to the given system.
\(\begin{array}{l} y<\frac{1}{4}x+2 \\ y\geq -4x+1 \\ (6,2),\: (-4,2),\: (9,1) \end{array}\)
\(\begin{array}{l} y\leq x+1 \\ y>-\frac{1}{4}x-2 \\ (-5,1),\: (10,1),\: (4,-2) \end{array}\)
\(\begin{array}{l} y<2x-1 \\ y\geq -x-2 \\ (2,-1),\: (-1,-1),\: (-5,-2) \end{array}\)
Solve each system by graphing.
\(\begin{array}{l} y>\frac{1}{4}x-1 \\ y<-\frac{1}{2}x+1 \end{array}\)
\(\begin{array}{l} y<2x+1 \\ y>-\frac{1}{2}x+2 \end{array}\)
\(\begin{array}{l} y<4x-2 \\ y>-2x-1 \end{array}\)
\(\begin{array}{l} y>\frac{1}{2}x-2 \\ y<-\frac{1}{4}x+2 \end{array}\)
\(\begin{array}{l} x\leq 6 \\ y<4 \end{array}\)
\(\begin{array}{l} x>-2 \\ y>4 \end{array}\)
\(\begin{array}{l} x\leq 3 \\ y>-2x+5 \end{array}\)
\(\begin{array}{l} x\leq 2 \\ y>-4x+5 \end{array}\)
\(\begin{array}{l} y<2x+2 \\ y>-4x-1 \end{array}\)
\(\begin{array}{l} y>2x-2 \\ y<-x+2 \end{array}\)
\(\begin{array}{l} 2x+y\geq 6 \\ 2x+5y\leq 10 \end{array}\)
\(\begin{array}{l} -2x-y\geq 6 \\ -2x-3y\leq 6 \end{array}\)
\(\begin{array}{l} -2x+y\geq -6 \\ -2x+5y\leq -10 \end{array}\)
\(\begin{array}{l} 2x-y\leq -4 \\ -x+5y\geq -5 \end{array}\)


