4.5: Systems of three linear equations in three variables
- Page ID
- 45048
Solving systems of linear equations in three variables is very similar to the methods in which we solve linear systems in two variables. With linear systems in two variables, we reduced the system down to one linear equation in one variable (by substitution or addition). With linear systems in three variables, we apply the same method except we reduce the system down from three linear equations in three variables to two linear equations in two variables first, then to one linear equation in one variable.
A system of three linear equations in three variables is given in the form \[\left\{\begin{array}{ll}ax+by+cz&=d \\ ex+fy+gz&=h \\ ix+jy+kz&=\ell \end{array}\right.\nonumber\] where \(a,\: b,\: c,\: d,\: e,\: f,\: g,\: h,\: i,\: j,\: k\) and \(\ell\) are coefficients and \(x,\: y,\) and \(z\) are variables. This system is represented in standard form.
Verifying Solutions
As we did is the previous section for verifying solutions with two linear equations in two variables, we can verify whether an ordered triple is a solution to the system of linear equations in three variables.
Determine whether \((5, −3, −4)\) is a solution to the system: \[\left\{\begin{array}{l}x+y+z=-2 \\ x+2y-3z=12 \\ 2x-2y+z=-9\end{array}\right.\nonumber\]
Solution
To verify whether \((5, −3, −4)\) is the solution to the system, we plug-n-chug \((5, −3, −4)\) into each equation and determine whether we obtain a true statement. If we obtain true statements for all equations in the system, then \((5, −3, −4)\) will be the solution to the system.
\[\begin{array}{rl}x+y+z=-2 &\text{Plug-n-chug }x=5,\: y=-3\text{ and }z=-4 \\ \color{blue}{5}\color{black}{}+(\color{blue}{-3}\color{black}{})+(\color{blue}{-4}\color{black}{})\stackrel{?}{=}-2&\text{Simplify} \\ 5-3-4\stackrel{?}{=}-2&\text{Subtract} \\ -2=-2&\checkmark\text{ True}\end{array}\nonumber\]
Let’s do the same for the second equation:
\[\begin{array}{rl}x+2y-3z=12&\text{Plug-n-chug }x=5,\: y=-3\text{ and }z=-4 \\ \color{blue}{5}\color{black}{}+2(\color{blue}{-3}\color{black}{})-3(\color{blue}{-4}\color{black}{})\stackrel{?}{=}12&\text{Simplify} \\ 11=12&X\text{ False}\end{array}\nonumber\]
Since the ordered triple \((5, −3, −4)\) makes the second equation false, then \((5, −3, −4)\) is not the solution to the system.
Let’s try a different ordered triple. Determine whether \((−1, 2, −3)\) is a solution to the system: \[\left\{\begin{array}{l}x+y+z=-2 \\ x+2y-3z=12 \\ 2x-2y+z=-9\end{array}\right.\nonumber\]
Solution
To verify whether \((−1, 2, −3)\) is the solution to the system, we plug-n-chug \((−1, 2, −3)\) into each equation and determine whether we obtain a true statement. If we obtain true statements for all equations in the system, then \((−1, 2, −3)\) will be the solution to the system.
\[\begin{array}{rl}x+y+z=-2 &\text{Plug-n-chug }x=-1,\: y=2\text{ and }z=-3 \\ \color{blue}{-1}\color{black}{}+\color{blue}{2}\color{black}{}+(\color{blue}{-3}\color{black}{})\stackrel{?}{=}-2&\text{Simplify} \\ -2=-2&\checkmark\text{ True}\end{array}\nonumber\]
Let’s do the same for the second equation:
\[\begin{array}{rl}x+2y-3z=12&\text{Plug-n-chug }x=-1,\: y=2\text{ and }z=-3 \\ \color{blue}{-1}\color{black}{}+2(\color{blue}{2}\color{black}{})-3(\color{blue}{-3}\color{black}{})\stackrel{?}{=}12&\text{Simplify} \\ 12=12&\checkmark\text{ True}\end{array}\nonumber\]
Let’s do the same for the third equation:
\[\begin{array}{rl}2x-2y+z=-9&\text{Plug-n-chug }x=-1,\: y=2\text{ and }z=-3 \\ 2(\color{blue}{-1}\color{black}{})-2(\color{blue}{2}\color{black}{})+(\color{blue}{-3}\color{black}{})\stackrel{?}{=}-9&\text{Simplify} \\ -9=-9&\checkmark\text{ True}\end{array}\nonumber\]
Since the ordered triple \((−1, 2, −3)\) makes all equations in the system true, then \((−1, 2, −3)\) is a solution to the system.
Solving Systems of Three Linear Equations in Three Variables
In Example 4.5.2 , we determined that the ordered tripe \((-1, 2, -3)\) is a solution to the system
\[\left\{\begin{array}{l}x+y+z=-2 \\ x+2y-3z=12 \\ 2x-2y+z=-9\end{array}\right.\nonumber\]
What does this mean? With systems of two linear equations in two variables, we know that if the system is consistent with an independent solution, then the solution is an ordered pair and two lines intersect. However, with three linear equations in three variables, what does a system that is consistent with an independent solution look like? We do know the answer is an ordered triple of form \((x, y, z)\), but what does the graph look like? Well, let’s take a look.
If we obtain a consistent system with an independent solution, then the solution is an ordered triple. This unique ordered triple represents the intersection of three planes.
However, experience from the previous sections tells us that this isn’t always the case, right? With two linear equations in two variables, we have two special cases: no solution and infinitely many solutions on line \(y = mx + b\).
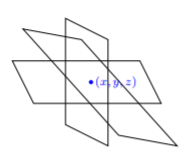
Recall. No solution meant the two lines were parallel and never intersected. Infinitely many solutions on line \(y = mx + b\) meant that the two lines were, in fact, the same line \(y = mx + b\).
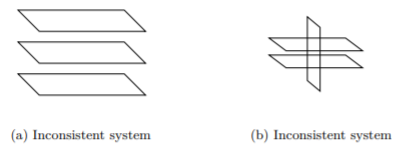
Let us take look at two cases with systems that are inconsistent, but now with three linear equations in three variable and with planes.
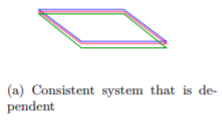
Lastly, let us take look at a case with a consistent system that is dependent, but now with three linear equations in three variable and with planes.
Solve the system: \[\left\{\begin{array}{l}3x+2y-z=-1 \\ -2x-2y+3z=5 \\ 5x+2y-z=3\end{array}\right.\nonumber\]
Solution
Let’s go ahead and number each equation so that we can identify each equation.
\[\begin{align}3x+2y-z=-1& \tag{1} \\ -2x-2y+3z=5 &\tag{2} \\ 5x+2y-z=3 &\tag{3} \end{align}\]
First, we choose a variable to eliminate. Then take two equations, say (1) and (2), and eliminate the chosen variable. Let’s choose \(y\) since we can see that the coefficients of \(y\) are the same and we can easily eliminate it.
\[\begin{align} 3x+2y-z=-1& \tag{1} \\ -2x-2y+3z=5& \tag{2}\end{align}\]
Adding (1) and (2), we obtain
\[\begin{align} x+2z=4& \tag{4}\end{align}\]
Now, let’s take equations (2) and (3) and eliminate \(y\) again:
\[\begin{align} -2x-2y+3z=5 &\tag{2} \\ 5x+2y-z=3 &\tag{3} \end{align}\]
Adding (2) and (3), we obtain
\[\begin{align} 3x+2z=8& \tag{5}\end{align}\]
Next, take equations (4) and (5). Notice, we have a system of two linear equations in two variables:
\[\begin{align} x+2z=4& \tag{4} \\ 3x+2z=8&\tag{5}\end{align}\]
We use the same process as we did in the previous section to obtain the solution for \(x\) and \(z\). Then substitute those values into one of the original equations to obtain \(y\). Thus, obtaining the ordered triple solution.
Let’s choose to eliminate \(z\) and solve for \(x\). First, let’s multiply equation (4) by \(−1\).
\[\begin{align} \color{blue}{-1}\color{black}{}(x+2z)&=\color{blue}{-1}\color{black}{}(4) \tag{4} \\ 3x+2z&=8 \tag{5}\end{align}\]
Now, we can solve for \(x\):
\[\begin{align} -x-2z&=-4 \tag{4} \\ 3x+2z&=8\tag{5}\end{align}\]
Adding these together, we get
\[\begin{aligned}2x&=4 \\ x&=2\end{aligned}\]
If \(x = 2\), then this implies that \(z = 1\), i.e.,
\[\begin{align} x+2z&=4 \tag{4} \\ \color{blue}{2}\color{black}{}+2z&=4\nonumber \\ 2z&=2\nonumber \\ z&=1\nonumber \end{align}\]
Lastly, we take \(x = 2\) and \(z = 1\) and substitute them into one of the original equations, like (1), and solve for \(y\):
\[\begin{align} 3x+2y-z&=-1 \tag{1} \\ 3\color{blue}{(2)}\color{black}{}+2y-\color{blue}{(1)}\color{black}{}&=-1\nonumber \\ 6+2y-1&=-1\nonumber \\ 5+2y&=-1\nonumber \\ 2y&=-6\nonumber \\ y&=-3\nonumber \end{align}\]
Thus, the point of intersection of the three planes is the ordered triple \((2, −3, 1)\).
Around 250 BCE, The Nine Chapters on the Mathematical Art were published in China. This book had 246 problems, and Chapter 8 was about solving systems of equations. One problem had four equations with five variables!
Special Cases
Looking back at Figure 1.2, we see that there are two special cases: Inconsistent systems and consistent systems with dependent solutions. Let’s us see examples of these special cases.
Solve the system: \[\left\{\begin{array}{l}5x-4y+3z=-4 \\ -10x+8y-6z=8 \\ 15x-12y+9z=-12\end{array}\right.\nonumber\]
Solution
Let’s go ahead and number each equation so that we can identify each equation.
\[\begin{align}5x-4y+3z&=-4 \tag{1} \\ -10x+8y-6z&=8 \tag{2} \\ 15x-12y+9z&=-12 \tag{3}\end{align}\]
First, we choose a variable to eliminate. Then take two equations, say (1) and (2), and eliminate the chosen variable. Let’s choose \(z\) since we can see that the coefficients of \(z\) are almost the same and we can easily eliminate it. We first multiply equation (1) by \(2\) and then add.
\[\begin{align}\color{blue}{2}\color{black}{}(5x-4y+3z)&=\color{blue}{2}\color{black}{}(-4)\tag{1} \\ -10x+8y-6z&=8\tag{2}\end{align}\]
Now, we can add to eliminate \(z\):
\[\begin{align}10x-8y+6z&=-8 \tag{1} \\ -10x+8y-6z&=8\tag{2} \end{align}\]
Adding (1) and (2), we obtain
\[0=0\quad\checkmark\text{ True}\nonumber\]
Since all variables eliminate and we are left with a true statement, we know this is a consistent system with dependent solutions. However, what is the solution? We see from Figure 4.5.3 a that this means all three planes are the same plane. Hence, we should write the solution as \(\{(x, y, z)|5x − 4y + 3z = −4\}\).
Solve the system: \[\left\{\begin{array}{l}3x-4y+z=2 \\ -9x+12y-3z=-5 \\ 4x-2y-z=3\end{array}\right.\nonumber\]
Solution
Let’s go ahead and number each equation so that we can identify each equation.
\[\begin{align} 3x-4y+z=2&\tag{1} \\ -9x+12y-3z=-5&\tag{2} \\ 4x-2y-z=3&\tag{3}\end{align}\]
First, we choose a variable to eliminate. Then take two equations, say (1) and (2), and eliminate the chosen variable. Let’s choose \(x\) since we can see that the coefficients of \(x\) are almost the same and we can easily eliminate it. We first multiply equation (1) by \(3\) and then add.
\[\begin{align}\color{blue}{3}\color{black}{}(3x-4y+z)&=\color{blue}{3}\color{black}{}(2) \tag{1} \\ -9x+12y-3z&=-5\tag{2}\end{align}\]
Now, we can add to eliminate \(z\):
\[\begin{align}9x-12y+3z&=6\tag{1} \\ -9x+12y-3z&=-5\tag{2}\end{align}\]
Adding (1) and (2), we obtain
\[0=1\quad X\text{ False}\nonumber\]
Since all variables eliminate and we are left with a false statement, we know this is an inconsistent system and there is no solution.
Systems of equations in three (or more) variables are not any more difficult than systems of equations in two variables as long as we are careful to keep organized. It is possible to solve each system several different ways. We can use different pairs of equations or eliminate variables in a different order. In a future chapter, we have the opportunity to solve systems of nonlinear equations!
Systems of Three Linear Equations in Three Variables Homework
Solve each system. Determine if each system is consistent, independent or dependent, or inconsistent. Write the solution as an ordered triple, if possible.
\(\begin{array}{l} a − 2b + c = 5\\ 2a + b − c = −1 \\ 3a + 3b − 2c = −4\end{array}\)
\(\begin{array}{l} 3x + y − z = 11 \\ x + 3y = z + 13 \\ x + y − 3z = 11 \end{array}\)
\(\begin{array}{l} x + 6y + 3z = 4 \\ 2x + y + 2z = 3 \\ 3x − 2y + z = 0 \end{array}\)
\(\begin{array}{l} x + y + z = 6 \\ 2x − y − z = −3 \\ x − 2y + 3z = 6 \end{array}\)
\(\begin{array}{l} x + y − z = 0 \\ x − y − z = 0 \\ x + y + 2z = 0 \end{array}\)
\(\begin{array}{l} −2x + y − 3z = 1 \\ x − 4y + z = 6 \\ 4x + 16y + 4z = 24 \end{array}\)
\(\begin{array}{l} 2x + y − 3z = 0 \\ x − 4y + z = 0 \\ 4x + 16y + 4z = 0 \end{array}\)
\(\begin{array}{l} 3x + 2y + 2z = 3 \\ x + 2y − z = 5 \\ 2x − 4y + z = 0 \end{array}\)
\(\begin{array}{l} x − 2y + 3z = 4 \\ 2x − y + z = −1 \\ 4x + y + z = 1 \end{array}\)
\(\begin{array}{l} x − y + 2z = 0 \\ x − 2y + 3z = −1 \\ 2x − 2y + z = −3 \end{array}\)
\(\begin{array}{l} 4x − 3y + 2z = 40 \\ 5x + 9y − 7z = 47 \\ 9x + 8y − 3z = 97 \end{array}\)
\(\begin{array}{l} 2x + 3y = z − 1 \\ 3x = 8z − 1 \\ 5y + 7z = −1 \end{array}\)
\(\begin{array}{l} x + y + z = 2 \\ 6x − 4y + 5z = 31 \\ 5x + 2y + 2z = 13 \end{array}\)
\(\begin{array}{l} x − y + 2z = −3 \\ x + 2y + 3z = 4 \\ 2x + y + z = −3 \end{array}\)
\(\begin{array}{l} x + y − z = 0 \\ x + 2y − 4z = 0 \\ 2x + y + z = 0 \end{array}\)
\(\begin{array}{l} x + 2y − z = 4 \\ 4x − 3y + z = 8 \\ 5x − y = 12 \end{array}\)
\(\begin{array}{l} 4x + 12y + 16z = 4 \\ 3x + 4y + 5z = 3 \\ x + 8y + 11z = 1 \end{array}\)
\(\begin{array}{l} 4x + 12y + 16z = 0 \\ 3x + 4y + 5z = 0 \\ x + 8y + 11z = 0 \end{array}\)
\(\begin{array}{l} p + q + r = 1 \\ p + 2q + 3r = 4 \\ 4p + 5q + 6r = 7 \end{array}\)
\(\begin{array}{l} x + 2y − 3z = 9 \\ 2x − y + 2z = −8 \\ 3x − y − 4z = 3 \end{array}\)
\(\begin{array}{l} 4x − 7y + 3z = 1 \\ 3x + y − 2z = 4 \\ 4x − 7y + 3z = 6 \end{array}\)
\(\begin{array}{l} 3x + y − z = 10 \\ 8x − y − 6z = −3 \\ 5x − 2y − 5z = 1 \end{array}\)
\(\begin{array}{l} 3x + 3y − 2z = 13 \\ 6x + 2y − 5z = 13 \\ 5x − 2y − 5z = −1 \end{array}\)
\(\begin{array}{l} 3x − 4y + 2z = 1 \\ 2x + 3y − 3z = −1 \\ x + 10y − 8z = 7 \end{array}\)
\(\begin{array}{l} m + 6n + 3p = 8 \\ 3m + 4n = −3 \\ 5m + 7n = 1 \end{array}\)
\(\begin{array}{l} 2x − 3y + 5z = 1 \\ 3x + 2y − z = 4 \\ 4x + 7y − 7z = 7 \end{array}\)
\(\begin{array}{l} 2x + y = z \\ 4x + z = 4y \\ y = x + 1 \end{array}\)
\(\begin{array}{l} 3x + 2y = z + 2 \\ y = 1 − 2x \\ 3z = −2y \end{array}\)
\(\begin{array}{l} −2w + 2x + 2y − 2z = −10 \\ w + x + y + z = −5 \\ 3w + 2x + 2y + 4z = −11 \\ w + 3x − 2y + 2z = −6 \end{array}\)
\(\begin{array}{l} w + x + y + z = 2 \\ w + 2x + 2y + 4z = 1 \\ −w + x − y − z = −6 \\ −w + 3x + y − z = −2 \end{array}\)
\(\begin{array}{l} −w + 2x − 3y + z = −8 \\ −w + x + y − z = −4 \\ w + x + y + z = 22 \\ −w + x − y − z = −14 \end{array}\)
\(\begin{array}{l} w + x − y + z = 0 \\ −w + 2x + 2y + z = 5 \\ −w + 3x + y − z = −4 \\ −2w + x + y − 3z = −7 \end{array}\)