11.5: Quadratic inequalities

Last updated
Save as PDF

Page ID: 45114

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

We can think about an earlier chapter where we obtained solutions for linear inequalities where the solutions are intervals of numbers. With quadratic inequalities, it is similar to linear inequalities, but, now, instead of lines, we have parabolas. Hence, we have two methods for solving quadratic inequalities: graphing or algebraically.

Solving Quadratic Inequalities by Graphing

Note

We can use the zeros (or roots) of a graph of a quadratic equation to solve for quadratic inequalities. Recall, the zeros (or roots) of a graph are the \(x\)-intercepts, i.e., \(y = 0\).

Example 11.5.1

Solve \(x^2 − 3x − 4\geq 0\) by using the graphing method.

Solution

We first begin by graphing \(x^2 − 3x − 4\) as we would in the previous section. Recall, the \(x\)-coordinate of the vertex is \(−\dfrac{b}{2a}\). Hence,

\[-\dfrac{b}{2a}=-\dfrac{-3}{2(1)}=\dfrac{3}{2}=1.5\nonumber\]

The \(y\)-coordinate of the vertex is \(x^2 − 3x − 4\) evaluated for \(x = 1.5\):

\[(1.5)^2-3(1.5)-4=-6.25\nonumber\]

The vertex is at \((1.5, −6.25)\). The \(y\)-intercept is when \(x = 0\):

\[0^2-3(0)-4=-4\nonumber\]

and the \(x\)-intercepts are when \(x^2 − 3x − 4 = 0\). Solving for the roots we get

\[\begin{aligned}x^2-3x-4&=0 \\ (x-4)(x+1)&=0 \\ x-4=0\quad&\text{or}\quad x+1=0 \\ x=4\quad&\text{or}\quad x=-1\end{aligned}\]

Thus, the intercepts are \((0, −4),\: (4, 0),\) and \((−1, 0)\) with a vertex at \((1.5, −6.25)\). Now we draw the graph:

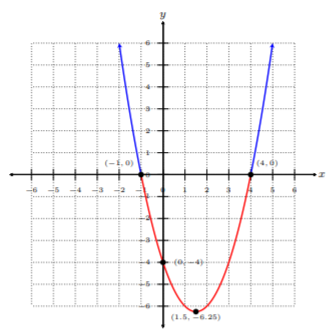
Given \(x^2 − 3x − 4\geq 0\) says we are specifically looking for the values of \(x^2 − 3x − 4\) in which are greater than or equal to zero. In other words, we are looking for all \(y\)-values that are above the \(x\)-axis because that is where all the \(y\)-values are positive. Looking at the graph above, these are all the values on the blue parts of the graph. Thus, using the graphing method, the solution is \((−∞, −1] ∪ [4, ∞)\). Note, we use brackets since it is \(\geq\).

Notice, we ignore the red part of the parabola since this is where \(x^2 − 3x − 4\) is negative, i.e., all the \(y\)-values are negative, because we were only looking for when \(x^2 − 3x − 4\geq 0\), the parts of the graph above the \(x\)-axis.

Solving Quadratic Inequalities Algebraically

The next method to solving quadratic inequalities is algebraically. Hence, there is a little more work involved since the method is algebraic. We must follow an order of steps to obtain the correct solution. The good news is that these two methods are similar where we always use the \(x\)-intercepts to determine the intervals.

Steps to solving quadratic inequalities

Step 1. Rewrite the inequality so that \(ax^2 + bx + c\) is on one side and zero is on the other.

Step 2. Determine where the inequality is zero using any method appropriate.

Step 3. Use the \(x\)-values obtained in the previous step to label on a number line.

Step 4. Take test values to observe where the inequality is true.

If the inequality is \(< 0\) or \(\leq 0\), then the inequality is true where the test values are negative.
If the inequality is \(> 0\) or \(\geq 0\), then the inequality is true where the test values are positive.

Step 5. Write the solution in interval notation.

Example 11.5.2

Solve algebraically: \(-x^2+8>2x\)

Solution

Step 1. We rewrite \(−x^2 + 8 > 2x\) so that zero is on one side: \[-x^2-2x+8>0\nonumber\]

Step 2. We set the left side equal to zero to obtain the roots (or zeros): \[\begin{aligned} -x^2-2x+8&=0 \\ x^2+2x-8&=0 \\ (x+4)(x-2)&=0 \\ x+4=0\quad&\text{or}\quad x-2=0 \\ x=-4\quad&\text{or}\quad x=2\end{aligned}\]

Step 3. Label \(-4\) and \(2\) on a blank number line:

Step 4. We take test values on each side of \(−4\) and \(2\). Let’s choose fairly easy numbers such as \(−5,\: 0\), and \(3\). We plug these numbers into \(−x^2 − 2x + 8\) and determine whether the value is positive or negative:

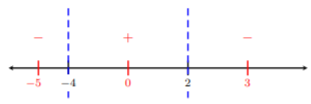
\[\begin{aligned} -(-5)^2-2(-5)+8&=-7<0\quad\Longrightarrow\quad\text{letting }x=-5 \\ -(0)^2-2(0)+8&=8>0\quad\Longrightarrow\quad\text{letting }x=0 \\ -(3)^2-2(3)+8&=-7<0\quad\Longrightarrow\quad\text{letting }x=3\end{aligned}\]

Step 5. Since \(−x^2 − 2x + 8 > 0\) (from Step 1.), then we are looking for where the test values are positive. Looking at the number line above, we see these are the values in between \(−4\) and \(2\). Thus, the solution is \((−4, 2)\). Note, we use parenthesis since the inequality symbol is \(>\).

Quadratic Inequalities Homework

Solve the inequality. Write the solution in interval notation.

Exercise 11.5.1

\(x^2-9x+18>0\)

Exercise 11.5.2

\(x^2-2x-24\leq 0\)

Exercise 11.5.3

\(x^2-2x-3<0\)

Exercise 11.5.4

\(x^2+10x+24\geq 0\)

Exercise 11.5.5

\(x^2-4x+4>0\)

Exercise 11.5.6

\(x^2+2x\geq 8\)

Exercise 11.5.7

\(x^2-4x\leq -3\)

Exercise 11.5.8

\(3x^2+7x-20\leq 0\)

Exercise 11.5.9

\(4x^2+11x-20\geq 0\)

Exercise 11.5.10

\(3x^2+2x-1<0\)

Exercise 11.5.11

\(-4x^2+7x\geq 0\)

Exercise 11.5.12

\(x^2+6x\geq 0\)

Exercise 11.5.13

\(x^2-12x+36<0\)

Exercise 11.5.14

\(x^2-2x+1\geq 0\)