6.7: Inverse and Implicit Functions. Open and Closed Maps
- Page ID
- 21628
I. "If \(f \in C D^{1}\) at \(\vec{p},\) then \(f\) resembles a linear map (namely \(d f )\) at \(\vec{p}."\) Pursuing this basic idea, we first make precise our notion of "\(f \in C D^{1}\) at \(\vec{p}\)."
A map \(f : E^{\prime} \rightarrow E\) is continuously differentiable, or of class \(C D^{1}\) (written \(f \in C D^{1}),\) at \(\vec{p}\) iff the following statement is true:
\[\begin{array}{l}{\text { Given any } \varepsilon>0, \text { there is } \delta>0 \text { such that } f \text { is differentiable on the }} \\ {\text { globe } \overline{G}=\overline{G_{\vec{p}}(\delta)}, \text { with }} \\ {\qquad\|d f(\vec{x} ; \cdot)-d f(\vec{p} ; \cdot)\|<\varepsilon \text { for all } \vec{x} \in \overline{G}.}\end{array}\]
By Problem 10 in §5, this definition agrees with Definition 1 §5, but is no longer limited to the case \(E^{\prime}=E^{n}\left(C^{n}\right).\) See also Problems 1 and 2 below.
We now obtain the following result.
Let \(E^{\prime}\) and \(E\) be complete. If \(f : E^{\prime} \rightarrow E\) is of class \(C D^{1}\) at \(\vec{p}\) and if \(d f(\vec{p} ; \cdot)\) is bijective (§6), then \(f\) is one-to-one on some globe \(\overline{G}=\overline{G_{\vec{p}}}(\delta).\)
Thus \(f\) "locally" resembles df \((\vec{p} ; \cdot)\) in this respect.
- Proof
-
Set \(\phi=d f(\vec{p} ; \cdot)\) and
\[\left\|\phi^{-1}\right\|=\frac{1}{\varepsilon}\]
(cf. Theorem 2 of §6).
By Definition 1, fix \(\delta>0\) so that for \(\vec{x} \in \overline{G}=\overline{G_{\vec{p}}(\delta)}\).
\[\|d f(\vec{x} ; \cdot)-\phi\|<\frac{1}{2} \varepsilon.\]
Then by Note 5 in §2,
\[(\forall \vec{x} \in \overline{G})\left(\forall \vec{u} \in E^{\prime}\right) \quad|d f(\vec{x} ; \vec{u})-\phi(\vec{u})| \leq \frac{1}{2} \varepsilon|\vec{u}|.\]
Now fix any \(\vec{r}, \vec{s} \in \overline{G}, \vec{r} \neq \vec{s},\) and set \(\vec{u}=\vec{r}-\vec{s} \neq 0.\) Again, by Note 5 in §2,
\[|\vec{u}|=\left|\phi^{-1}(\phi(\vec{u}))\right| \leq\left\|\phi^{-1}\right\||\phi(\vec{u})|=\frac{1}{\varepsilon}|\phi(\vec{u})|;\]
so
\[0<\varepsilon|\vec{u}| \leq|\phi(\vec{u})|.\]
By convexity, \(\overline{G} \supseteq I=L[\vec{s}, \vec{r}],\) so (1) holds for \(\vec{x} \in I, \vec{x}=\vec{s}+t \vec{u}, 0 \leq t \leq 1\).
Noting this, set
\[h(t)=f(\vec{s}+t \vec{u})-t \phi(\vec{u}), \quad t \in E^{1}.\]
Then for \(0 \leq t \leq 1\),
\[\begin{aligned} h^{\prime}(t) &=D_{\vec{u}} f(\vec{s}+t \vec{u})-\phi(\vec{u}) \\ &=d f(\vec{s}+t \vec{u} ; \vec{u})-\phi(\vec{u}). \end{aligned}\]
(Verify!) Thus by (1) and (2),
\[\begin{aligned} \sup _{0 \leq t \leq 1}\left|h^{\prime}(t)\right| &=\sup _{0 \leq t \leq 1}|d f(\vec{s}+t \vec{u} ; \vec{u})-\phi(\vec{u})| \\ & \leq \frac{\varepsilon}{2}|\vec{u}| \leq \frac{1}{2}|\phi(\vec{u})|. \end{aligned}\]
(Explain!) Now, by Corollary 1 in Chapter 5, §4,
\[|h(1)-h(0)| \leq(1-0) \cdot \sup _{0 \leq t \leq 1}\left|h^{\prime}(t)\right| \leq \frac{1}{2}|\phi(\vec{u})|.\]
As \(h(0)=f(\vec{s})\) and
\[h(1)=f(\vec{s}+\vec{u})-\phi(\vec{u})=f(\vec{r})-\phi(\vec{u}),\]
we obtain (even if \(\vec{r}=\vec{s})\)
\[|f(\vec{r})-f(\vec{s})-\phi(\vec{u})| \leq \frac{1}{2}|\phi(\vec{u})| \quad(\vec{r}, \vec{s} \in \overline{G}, \vec{u}=\vec{r}-\vec{s}).\]
But by the triangle law,
\[|\phi(\vec{u})|-|f(\vec{r})-f(\vec{s})| \leq|f(\vec{r})-f(\vec{s})-\phi(\vec{u})|.\]
Thus
\[|f(\vec{r})-f(\vec{s})| \geq \frac{1}{2}|\phi(\vec{u})| \geq \frac{1}{2} \varepsilon|\vec{u}|=\frac{1}{2} \varepsilon|\vec{r}-\vec{s}|\]
by (2).
Hence \(f(\vec{r}) \neq f(\vec{s})\) whenever \(\vec{r} \neq \vec{s}\) in \(\overline{G};\) so \(f\) is one-to-one on \(\overline{G},\) as claimed.\(\quad \square\)
Under the assumptions of Theorem 1, the maps \(f\) and \(f^{-1}\) (the inverse of \(f\) restricted to \(\overline{G}\)) are uniformly continuous on \(\overline{G}\) and \(f[\overline{G}],\) respectively.
- Proof
-
By (3),
\[\begin{aligned}|f(\vec{r})-f(\vec{s})| & \leq|\phi(\vec{u})|+\frac{1}{2}|\phi(\vec{u})| \\ & \leq|2 \phi(\vec{u})| \\ & \leq 2\|\phi\||\vec{u}| \\ &=2\|\phi\||\vec{r}-\vec{s}| \quad(\vec{r}, \vec{s} \in \overline{G}). \end{aligned}\]
This implies uniform continuity for \(f\). (Why?)
Next, let \(g=f^{-1}\) on \(H=f[\overline{G}]\).
If \(\vec{x}, \vec{y} \in H,\) let \(\vec{r}=g(\vec{x})\) and \(\vec{s}=g(\vec{y});\) so \(\vec{r}, \vec{s} \in \overline{G},\) with \(\vec{x}=f(\vec{r})\) and \(\vec{y}=f(\vec{s}).\) Hence by (4),
\[|\vec{x}-\vec{y}| \geq \frac{1}{2} \varepsilon|g(\vec{x})-g(\vec{y})|,\]
proving all for \(g,\) too.\(\quad \square\)
Again, \(f\) resembles \(\phi\) which is uniformly continuous, along with \(\phi^{-1}\).
II. We introduce the following definition.
A map \(f :(S, \rho) \rightarrow\left(T, \rho^{\prime}\right)\) is closed (open) on \(D \subseteq S\) iff, for any \(X \subseteq D\) the set \(f[X]\) is closed (open) in \(T\) whenever \(X\) is so in \(S.\)
Note that continuous maps have such a property for inverse images (Problem 15 in Chapter 4, §2).
Under the assumptions of Theorem 1, \(f\) is closed on \(\overline{G},\) and so the set \(f[\overline{G}]\) is closed in \(E.\)
Similarly for the map \(f^{-1}\) on \(f[\overline{G}]\).
- Proof for \(E^{\prime}=E=E^{n}\left(C^{n}\right)\) (for the general case, see Problem 6)
-
Given any closed \(X \subseteq \overline{G},\) we must show that \(f[X]\) is closed in \(E.\)
Now, as \(\overline{G}\) is closed and bounded, it is compact (Theorem 4 of Chapter 4, §6).
So also is \(X\) (Theorem 1 in Chapter 4, §6), and so is \(f[X]\) (Theorem 1 of Chapter 4, §8).
By Theorem 2 in Chapter 4, §6, \(f[X]\) is closed, as required.\(\quad \square\)
For the rest of this section, we shall set \(E^{\prime}=E=E^{n}\left(C^{n}\right)\).
If \(E^{\prime}=E=E^{n}\left(C^{n}\right)\) in Theorem 1, with other assumptions unchanged, then \(f\) is open on the globe \(G=G_{\vec{p}}(\delta),\) with \(\delta\) sufficiently small.
- Proof
-
We first prove the following lemma.
\(f[G]\) contains a globe \(G_{\vec{q}}(\alpha)\) where \(\vec{q}=f(\vec{p})\).
- Proof
-
Indeed, let
\[\alpha=\frac{1}{4} \varepsilon \delta,\]
where \(\delta\) and \(\varepsilon\) are as in the proof of Theorem 1. (We continue the notation and formulas of that proof.)
Fix any \(\vec{c} \in G_{\vec{q}}(\alpha);\) so
\[|\vec{c}-\vec{q}|<\alpha=\frac{1}{4} \varepsilon \delta.\]
Set \(h=|f-\vec{c}|\) on \(E^{\prime}.\) As \(f\) is uniformly continuous on \(\overline{G},\) so is \(h\).
Now, \(\overline{G}\) is compact in \(E^{n}\left(C^{n}\right);\) so Theorem 2(ii) in Chapter 4, §8, yields a point \(\vec{r} \in \overline{G}\) such that
\[h(\vec{r})=\min h[\overline{G}].\]
We claim that \(\vec{r}\) is in \(G\) (the interior of \(\overline{G})\).
Otherwise, \(|\vec{r}-\vec{p}|=\delta ;\) for by (4),
\[\begin{aligned} 2 \alpha=\frac{1}{2} \varepsilon \delta=\frac{1}{2} \varepsilon|\vec{r}-\vec{p}| & \leq|f(\vec{r})-f(\vec{p})| \\ & \leq|f(\vec{r})-\vec{c}|+|\vec{c}-f(\vec{p})| \\ &=h(\vec{r})+h(\vec{p}). \end{aligned}\]
But
\[h(\vec{p})=|\vec{c}-f(\vec{p})|=|\vec{c}-\vec{q}|<\alpha;\]
and so (7) yields
\[h(\vec{p})<\alpha<h(\vec{r}),\]
contrary to the minimality of \(h(\vec{r})\) (see (6)). Thus \(|\vec{r}-\vec{p}|\) cannot equal \(\delta\).
We obtain \(|\vec{r}-\vec{p}|<\delta,\) so \(\vec{r} \in G_{\vec{p}}(\delta)=G\) and \(f(\vec{r}) \in f[G].\) We shall now show that \(\vec{c}=f(\vec{r}).\)
To this end, we set \(\vec{v}=\vec{c}-f(\vec{r})\) and prove that \(\vec{v}=\overrightarrow{0}.\) Let
\[\vec{u}=\phi^{-1}(\vec{v}),\]
where
\[\phi=d f(\vec{p} ; \cdot),\]
as before. Then
\[\vec{v}=\phi(\vec{u})=d f(\vec{p} ; \vec{u}).\]
With \(\vec{r}\) as above, fix some
\[\vec{s}=\vec{r}+t \vec{u} \quad(0<t<1)\]
with \(t\) so small that \(\vec{s} \in G\) also. Then by formula (3),
\[|f(\vec{s})-f(\vec{r})-\phi(t \vec{u})| \leq \frac{1}{2}|t \vec{v}|;\]
also,
\[|f(\vec{r})-\vec{c}+\phi(t \vec{u})|=(1-t)|\vec{v}|=(1-t) h(\vec{r})\]
by our choice of \(\vec{v}, \vec{u}\) and \(h.\) Hence by the triangle law,
\[h(\vec{s})=|f(\vec{s})-\vec{c}| \leq\left(1-\frac{1}{2} t\right) h(\vec{r}).\]
(Verify!)
As \(0<t<1,\) this implies \(h(\vec{r})=0\) (otherwise, \(h(\vec{s})<h(\vec{r}),\) violating (6)).
Thus, indeed,
\[|\vec{v}|=|f(\vec{r})-\vec{c}|=0,\]
i.e.,
\[\vec{c}=f(\vec{r}) \in f[G] \quad \text { for } \vec{r} \in G.\]
But \(\vec{c}\) was an arbitrary point of \(G_{\vec{q}}(\alpha).\) Hence
\[G_{\vec{q}}(\alpha) \subseteq f[G],\]
proving the lemma.\(\quad \square\)
Proof of Theorem 2. The lemma shows that \(f(\vec{p})\) is in the interior of \(f[G]\) if \(\vec{p}, f, d f(\vec{p} ; \cdot),\) and \(\delta\) are as in Theorem 1.
But Definition 1 implies that here \(f \in C D^{1}\) on all of \(G\) (see Problem 1).
Also, \(d f(\vec{x} ; \cdot)\) is bijective for any \(\vec{x} \in G\) by our choice of \(G\) and Theorems 1 and 2 in §6.
Thus \(f\) maps all \(\vec{x} \in G\) onto interior points of \(f[G];\) i.e., \(f\) maps any open set \(X \subseteq G\) onto an open \(f[X],\) as required.\(\quad \square\)
Note 1. A map
\[f :(S, \rho) \underset{\text { onto }}{\longleftrightarrow} (T, \rho^{\prime})\]
is both open and closed ("clopen") iff \(f^{-1}\) is continuous - see Problem 15(iv)(v) in Chapter 4, §2, interchanging \(f\) and \(f^{-1}.\)
Thus \(\phi=d f(\vec{p} ; \cdot)\) in Theorem 1 is "clopen" on all of \(E^{\prime}\).
Again, \(f\) locally resembles \(d f(\vec{p} ; \cdot)\).
III. The Inverse Function Theorem. We now further pursue these ideas.
Under the assumptions of Theorem 2, let \(g\) be the inverse of \(f_{G}\left(f \text { restricted to } G=G_{\vec{p}}(\delta)\right)\).
Then \(g \in C D^{1}\) on \(f[G]\) and \(d g(\vec{y} ; \cdot)\) is the inverse of \(d f(\vec{x} ; \cdot)\) whenever \(\vec{x}=g(\vec{y}), \vec{x} \in G.\)
Briefly: "The differential of the inverse is the inverse of the differential."
- Proof
-
Fix any \(\vec{y} \in f[G]\) and \(\vec{x}=g(\vec{y}) ;\) so \(\vec{y}=f(\vec{x})\) and \(\vec{x} \in G.\) Let \(U=d f(\vec{x} ; \cdot).\)
As noted above, \(U\) is bijective for every \(\vec{x} \in G\) by Theorems 1 and 2 in §6; so we may set \(V=U^{-1}.\) We must show that \(V=d g(\vec{y} ; \cdot).\)
To do this, give \(\vec{y}\) an arbitrary (variable) increment \(\Delta \vec{y},\) so small that \(\vec{y}+\Delta \vec{y}\) stays in \(f[G]\) (an open set by Theorem 2).
As \(g\) and \(f_{G}\) are one-to-one, \(\Delta \vec{y}\) uniquely determines
\[\Delta \vec{x}=g(\vec{y}+\Delta \vec{y})-g(\vec{y})=\vec{t},\]
and vice versa:
\[\Delta \vec{y}=f(\vec{x}+\vec{t})-f(\vec{x}).\]
Here \(\Delta \vec{y}\) and \(\vec{t}\) are the mutually corresponding increments of \(\vec{y}=f(\vec{x})\) and \(\vec{x}=g(\vec{y}).\) By continuity, \(\vec{y} \rightarrow \overrightarrow{0}\) iff \(\vec{t} \rightarrow \overrightarrow{0}.\)
As \(U=d f(\vec{x} ; \cdot)\),
\[\lim _{\vec{t} \rightarrow \overline{0}} \frac{1}{|\vec{t}|}|f(\vec{x}+\vec{t})-f(\vec{t})-U(\vec{t})|=0,\]
or
\[\lim _{\vec{t} \rightarrow \overrightarrow{0}} \frac{1}{|\vec{t}|}|F(\vec{t})|=0,\]
where
\[F(\vec{t})=f(\vec{x}+\vec{t})-f(\vec{t})-U(\vec{t}).\]
As \(V=U^{-1},\) we have
\[V(U(\vec{t}))=\vec{t}=g(\vec{y}+\Delta \vec{y})-g(\vec{y}).\]
So from (9),
\[\begin{aligned} V(F(\vec{t})) &=V(\Delta \vec{y})-\vec{t} \\ &=V(\Delta \vec{y})-[g(\vec{y}+\Delta \vec{y})-g(\vec{y})]; \end{aligned}\]
that is,
\[\frac{1}{|\Delta \vec{y}|}|g(\vec{y}+\Delta \vec{y})-g(\vec{y})-V(\Delta \vec{y})|=\frac{|V(F(\vec{t}))|}{|\Delta \vec{y}|}, \quad \Delta \vec{y} \neq \overrightarrow{0}.\]
Now, formula (4), with \(\vec{r}=\vec{x}, \vec{s}=\vec{x}+\vec{t},\) and \(\vec{u}=\vec{t},\) shows that
\[|f(\vec{x}+\vec{t})-f(\vec{x})| \geq \frac{1}{2} \varepsilon|\vec{t}|;\]
i.e., \(|\Delta \vec{y}| \geq \frac{1}{2} \varepsilon|\vec{t}|.\) Hence by (8),
\[\frac{|V(F(\vec{t}))|}{|\Delta \vec{y}|} \leq \frac{|V(F(\vec{t}) |}{\frac{1}{2} \varepsilon|\vec{t}|}=\frac{2}{\varepsilon}\left|V\left(\frac{1}{|\vec{t}|} F(\vec{t})\right)\right| \leq \frac{2}{\varepsilon}\|V\| \frac{1}{|\vec{t}|}|F(\vec{t})| \rightarrow 0 \text { as } \vec{t} \rightarrow \overrightarrow{0}.\]
Since \(\vec{t} \rightarrow \overrightarrow{0}\) as \(\Delta \vec{y} \rightarrow \overrightarrow{0}\) (change of variables!), the expression (10) tends to 0 as \(\Delta \vec{y} \rightarrow \overrightarrow{0}.\)
By definition, then, \(g\) is differentiable at \(\vec{y},\) with \(d g(\vec{y};)=V=U^{-1}\).
Moreover, Corollary 3 in §6, applies here. Thus
\[\left(\forall \delta^{\prime}>0\right)\left(\exists \delta^{\prime \prime}>0\right) \quad\|U-W\|<\delta^{\prime \prime} \Rightarrow\left\|U^{-1}-W^{-1}\right\|<\delta^{\prime}.\]
Taking here \(U^{-1}=d g(\vec{y})\) and \(W^{-1}=d g(\vec{y}+\Delta \vec{y}),\) we see that \(g \in C D^{1}\) near \(\vec{y}.\) This completes the proof.\(\quad \square\)
Note 2. If \(E^{\prime}=E=E^{n}\left(C^{n}\right),\) the bijectivity of \(\phi=d f(\vec{p} ; \cdot)\) is equivalent to
\[\operatorname{det}[\phi]=\operatorname{det}\left[f^{\prime}(\vec{p})\right] \neq 0\]
(Theorem 1 of §6).
In this case, the fact that \(f\) is one-to-one on \(G=G_{\vec{p}}(\delta)\) means, componentwise (see Note 3 in §6), that the system of \(n\) equations
\[f_{i}(\vec{x})=f\left(x_{1}, \ldots, x_{n}\right)=y_{i}, \quad i=1, \ldots, n,\]
has a unique solution for the \(n\) unknowns \(x_{k}\) as long as
\[\left(y_{1}, \ldots, y_{n}\right)=\vec{y} \in f[G].\]
Theorem 3 shows that this solution has the form
\[x_{k}=g_{k}(\vec{y}), \quad k=1, \ldots, n,\]
where the \(g_{k}\) are of class \(C D^{1}\) on \(f[G]\) provided the \(f_{i}\) are of class \(C D^{1}\) near \(\vec{p}\) and det \(\left[f^{\prime}(\vec{p})\right] \neq 0.\) Here
\[\operatorname{det}\left[f^{\prime}(\vec{p})\right]=J_{f}(\vec{p}),\]
as in §6.
Thus again \(f\) "locally" resembles a linear map, \(\phi=d f(\vec{p} ; \cdot)\).
IV. The Implicit Function Theorem. Generalizing, we now ask, what about solving \(n\) equations in \(n+m\) unknowns \(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}?\) Say, we want to solve
\[f_{k}\left(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}\right)=0, \quad k=1,2, \ldots, n,\]
for the first \(n\) unknowns (or variables) \(x_{k},\) thus expressing them as
\[x_{k}=H_{k}\left(y_{1}, \ldots, y_{m}\right), \quad k=1, \ldots, n,\]
with \(H_{k} : E^{m} \rightarrow E^{1}\) or \(H_{k} : C^{m} \rightarrow C\).
Let us set \(\vec{x}=\left(x_{1}, \ldots, x_{n}\right), \vec{y}=\left(y_{1}, \ldots, y_{m}\right),\) and
\[(\vec{x}, \vec{y})=\left(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}\right)\]
so that \((\vec{x}, \vec{y}) \in E^{n+m}\left(C^{n+m}\right)\).
Thus the system of equations (11) simplifies to
\[f_{k}(\vec{x}, \vec{y})=0, \quad k=1, \ldots, n\]
or
\[f(\vec{x}, \vec{y})=\overrightarrow{0},\]
where \(f=\left(f_{1}, \ldots, f_{n}\right)\) is a map of \(E^{n+m}\left(C^{n+m}\right)\) into \(E^{n}\left(C^{n}\right) ; f\) is a function of \(n+m\) variables, but it has \(n\) components \(f_{k};\) i.e.,
\[f(\vec{x}, \vec{y})=f\left(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}\right)\]
is a vector in \(E^{n}\left(C^{n}\right)\).
Let \(E^{\prime}=E^{n+m}\left(C^{n+m}\right), E=E^{n}\left(C^{n}\right),\) and let \(f : E^{\prime} \rightarrow E\) be of class \(C D^{1}\) near
\[(\vec{p}, \vec{q})=\left(p_{1}, \ldots, p_{n}, q_{1}, \ldots, q_{m}\right), \quad \vec{p} \in E^{n}\left(C^{n}\right), \vec{q} \in E^{m}\left(C^{m}\right).\]
Let \([\phi]\) be the \(n \times n\) matrix
\[\left(D_{j} f_{k}(\vec{p}, \vec{q})\right), \quad j, k=1, \ldots, n.\]
If \(\operatorname{det}[\phi] \neq 0\) and if \(f(\vec{p}, \vec{q})=\overrightarrow{0},\) then there are open sets
\[P \subseteq E^{n}\left(C^{n}\right) \text { and } Q \subseteq E^{m}\left(C^{m}\right),\]
with \(\vec{p} \in P\) and \(\vec{q} \in Q,\) for which there is a unique map
\[H : Q \rightarrow P\]
with
\[f(H(\vec{y}), \vec{y})=\overrightarrow{0}\]
for all \(\vec{y} \in Q;\) furthermore, \(H \in C D^{1}\) on \(Q\).
Thus \(\vec{x}=H(\vec{y})\) is a solution of (11) in vector form.
- Proof
-
With the above notation, set
\[F(\vec{x}, \vec{y})=(f(\vec{x}, \vec{y}), \vec{y}), \quad F : E^{\prime} \rightarrow E^{\prime}.\]
Then
\[F(\vec{p}, \vec{q})=(f(\vec{p}, \vec{q}), \vec{q})=(\overrightarrow{0}, \vec{q}),\]
since \(f(\vec{p}, \vec{q})=\overrightarrow{0}\).
As \(f \in C D^{1}\) near \((\vec{p}, \vec{q}),\) so is \(F\) (verify componentwise via Problem 9(ii) in §3 and Definition 1 of §5).
By Theorem 4, §3, \(\operatorname{det}\left[F^{\prime}(\vec{p}, \vec{q})\right]=\operatorname{det}[\phi] \neq 0\) (explain!).
Thus Theorem 1 above shows that \(F\) is one-to-one on some globe \(G\) about \((\vec{p}, \vec{q}).\)
Clearly \(G\) contains an open interval about \((\vec{p}, \vec{q}).\) We denote it by \(P \times Q\) where \(\vec{p} \in P, \vec{q} \in Q ; P\) is open in \(E^{n}\left(C^{n}\right)\) and \(Q\) is open in \(E^{m}\left(C^{m}\right).\)
By Theorem 3, \(F_{P \times Q}\) (\(F\) restricted to \(P \times Q)\) has an inverse
\[g : A \underset{\text { onto }}{\longleftrightarrow} P \times Q,\]
where \(A=F[P \times Q]\) is open in \(E^{\prime}\) (Theorem 2), and \(g \in C D^{1}\) on \(A.\) Let the map \(u=\left(g_{1}, \ldots, g_{n}\right)\) comprise the first \(n\) components of \(g\) (exactly as \(f\) comprises the first \(n\) components of \(F )\).
Then
\[g(\vec{x}, \vec{y})=(u(\vec{x}, \vec{y}), \vec{y})\]
exactly as \(F(\vec{x}, \vec{y})=(f(\vec{x}, \vec{y}), \vec{y}).\) Also, \(u : A \rightarrow P\) is of class \(C D^{1}\) on \(A,\) as \(g\) is (explain!).
Now set
\[H(\vec{y})=u(\overrightarrow{0}, \vec{y});\]
here \(\vec{y} \in Q,\) while
\[(\overrightarrow{0}, \vec{y}) \in A=F[P \times Q],\]
for \(F\) preserves \(\vec{y}\) (the last \(m\) coordinates). Also set
\[\alpha(\vec{x}, \vec{y})=\vec{x}.\]
Then \(f=\alpha \circ F\) (why?), and
\[f(H(\vec{y}), \vec{y})=f(u(\overrightarrow{0}, \vec{y}), \vec{y})=f(g(\overrightarrow{0}, \vec{y}))=\alpha(F(g(\overrightarrow{0}, \vec{y}))=\alpha(\overrightarrow{0}, \vec{y})=\overrightarrow{0}\]
by our choice of \(\alpha\) and \(g\) (inverse to \(F).\) Thus
\[f(H(\vec{y}), \vec{y})=\overrightarrow{0}, \quad \vec{y} \in Q,\]
as desired.
Moreover, as \(H(\vec{y})=u(\overrightarrow{0}, \vec{y}),\) we have
\[\frac{\partial}{\partial y_{i}} H(\vec{y})=\frac{\partial}{\partial y_{i}} u(\overrightarrow{0}, \vec{y}), \quad \vec{y} \in Q, i \leq m.\]
As \(u \in C D^{1},\) all \(\partial u / \partial y_{i}\) are continuous (Definition 1 in §5); hence so are the \(\partial H / \partial y_{i}.\) Thus by Theorem 3 in §3, \(H \in C D^{1}\) on \(Q.\)
Finally, \(H\) is unique for the given \(P, Q;\) for
\[\begin{aligned} f(\vec{x}, \vec{y})=\overrightarrow{0} & \Longrightarrow(f(\vec{x}, \vec{y}), \vec{y})=(\overrightarrow{0}, \vec{y}) \\ & \Longrightarrow F(\vec{x}, \vec{y})=(\overrightarrow{0}, \vec{y}) \\ & \Longrightarrow g(F(\vec{x}, \vec{y}))=g(\overrightarrow{0}, \vec{y}) \\ & \Longrightarrow(\vec{x}, \vec{y})=g(\overrightarrow{0}, \vec{y})=(u(\overrightarrow{0}, \vec{y}), \vec{y}) \\ & \Longrightarrow \vec{x}=u(\overrightarrow{0}, \vec{y})=H(\vec{y}). \end{aligned}\]
Thus \(f(\vec{x}, \vec{y})=\overrightarrow{0}\) implies \(\vec{x}=H(\vec{y});\) so \(H(\vec{y})\) is the only solution for \(\vec{x}. \quad \square\)
Note 3. \(H\) is said to be implicitly defined by the equation \(f(\vec{x}, \vec{y})=\overrightarrow{0}.\) In this sense we say that \(H(\vec{y})\) is an implicit function, given by \(f(\vec{x}, \vec{y})=\overrightarrow{0}\).
Similarly, under suitable assumptions, \(f(\vec{x}, \vec{y})=\overrightarrow{0}\) defines \(\vec{y}\) as a function of \(\vec{x}.\)
Note 4. While \(H\) is unique for a given neighborhood \(P \times Q\) of \((\vec{p}, \vec{q}),\) another implicit function may result if \(P \times Q\) or \((\vec{p}, \vec{q})\) is changed.
For example, let
\[f(x, y)=x^{2}+y^{2}-25\]
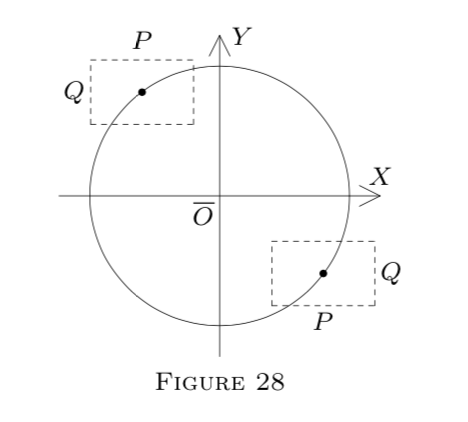
(a polynomial; hence \(f \in C D^{1}\) on all of \(E^{2}).\) Geometrically, \(x^{2}+y^{2}-25=0\) describes a circle.
Solving for \(x,\) we get \(x=\pm \sqrt{25-y^{2}}.\) Thus we have two functions:
\[H_{1}(y)=+\sqrt{25-y^{2}}\]
and
\[H_{2}(y)=-\sqrt{25-y^{2}}.\]
If \(P \times Q\) is in the upper part of the circle, the resulting function is \(H_{1}.\) Otherwise, it is \(H_{2}.\) See Figure 28.
V. Implicit Differentiation. Theorem 4 only states the existence (and uniqueness) of a solution, but does not show how to find it, in general.
The knowledge itself that \(H \in C D^{1}\) exists, however, enables us to use its derivative or partials and compute it by implicit differentiation, known from calculus.
(a) Let \(f(x, y)=x^{2}+y^{2}-25=0,\) as above.
This time treating \(y\) as an implicit function of \(x, y=H(x),\) and writing \(y^{\prime}\) for \(H^{\prime}(x),\) we differentiate both sides of (x^{2}+y^{2}-25=0\) with respect to \(x,\) using the chain rule for the term \(y^{2}=[H(x)]^{2}\).
This yields \(2 x+2 y y^{\prime}=0,\) whence \(y^{\prime}=-x / y\).
Actually (see Note 4), two functions are involved: \(y=\pm \sqrt{25-x^{2}};\) but both satisfy \(x^{2}+y^{2}-25=0;\) so the result \(y^{\prime}=-x / y\) applies to both.
Of course, this method is possible only if the derivative \(y^{\prime}\) is known to exist. This is why Theorem 4 is important.
(b) Let
\[f(x, y, z)=x^{2}+y^{2}+z^{2}-1=0, \quad x, y, z \in E^{1}.\]
Again \(f\) satisfies Theorem 4 for suitable \(x, y,\) and \(z\).
Setting \(z=H(x, y),\) differentiate the equation \(f(x, y, z)=0\) partially with respect to \(x\) and \(y.\) From the resulting two equations, obtain \(\frac{\partial z}{\partial x}\) and \(\frac{\partial z}{\partial y}\).